Черт. 29. К примеру расчета 18

Расчет. Согласно п. 3.38 проверим из усло­вия (50) наклонное сечение, начинающееся от места приложения сосредоточенной силы, при значении с, определяемом по формуле (68).

Рабочая высота в месте приложения сосредоточенной силы равна 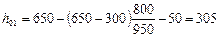мм (см. черт. 29).

По формуле (52) определим величину M_{b 1}, при­нимая j_{b 2} = 2 (см. табл. 21) и j_f = 0:

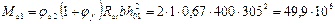Н · мм.

Значение q_sw равно:

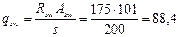Н/мм (кН/м).

Принимая 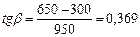(см. черт. 29), определим q_inc:

Н/мм,

отсюда, принимая q ₁ = 0, имеем

мм,

при этом c ₀ = c = 556 мм.

Поскольку значение с не превышает значения расстояния от груза до опоры, оставим с = 556 мм и определим рабочую высоту h ₀ в конце наклон­ного сечения:

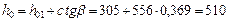мм.

Поскольку 2 h ₀ = 2 · 510 мм > c ₀ = 558 мм, оста­вим c ₀ = 556 мм.

Значение M_b равно:

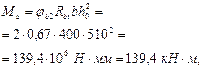
отсюда

т. е. прочность этого наклонного сечения обеспечена.

Для наклонного сечения, располагаемого от груза до опоры, по формуле (56) определим значение c ₀, принимая h ₀ = 650 – 50 = 600 мм:

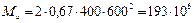Н · мм;

принимаем c ₀ = 2 h ₀ = 1200 мм.

Поскольку c ₀ = 1200 мм > с = 800 мм, указанное наклонное сечение можно не проверять. Следова­тельно, прочность любого наклонного сечения обеспечена.

Пример 19. Дано: сплошная плита перекрытия без поперечной арматуры размером 3х6 м, толщи­ной h = 160 мм, монолитно связанная по периметру с балками; эквивалентная временная равномерно распределенная нагрузка на плиту v = 50 кН/м²; нагрузка от собственного веса и пола g = 9 кН/м²; a = 20 мм; бетон тяжелый класса В25 (R_bt = 0,95 МПа при g _{b 2} = 0,9).

Требуется проверить прочность плиты на дей­ствие поперечной силы.

Расчет. h ₀ = h – а = 160 – 20 = 140 мм. Ра­счет производим для полосы шириной b = 1 м = 1000 мм, пролетом l = 3 м; полная нагрузка на плиту равна q = v + g = 50 + 9 = 59 кН/м.

Поперечная сила на опоре равна:

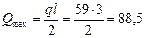кН.

Проверим условие (71):

Проверим условие (72). Поскольку боковые края плиты связаны с балками, значение c_max определим с учетом коэффициента a = 1 + 0,05 b/h = 1 + 0,05 · 6/0,16 > 1,25 (здесь b = 6 м — расстоя­ние между боковыми краями плиты), т. е. a = 1,25:

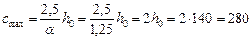мм.

Согласно п. 3.32 имеем:

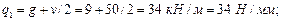
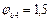(см. табл. 21).

Поскольку 356 Н/мм > q ₁ = 34 Н/мм, принимаем с = c_max = 280 мм = 0,28 м.

Поперечная сила в конце наклонного сечения равна Q = Q_max – q ₁ c = 88,5 – 34 · 0,28 = 79 кН.

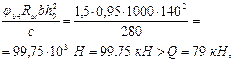
т. е. прочность плиты по поперечной силе обеспечена.

Пример 20. Дано: панель резервуара консоль­ного типа с переменной толщиной от 262 (в за­делке) до 120 мм (на свободном конце), вылетом 4,25 м; боковое давление грунта, учитывающее нагрузки от транспортных средств на поверхности грунта, линейно убывает от q ₀ = 69 кН/м² в задел­ке до q = 7 кН/м² на свободном конце; а = 22 мм; бетон тяжелый класса В15 (R_bt = 0,82 МПа при g _{b 2} = 1,1).

Требуется проверить прочность панели по поперечной силе.

Расчет. Рабочая высота сечения панели в за­делке равна h ₀₁ = 262 – 22 = 240мм.

Определим tg b (b — угол между растянутой и сжатой гранями):

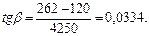
Расчет производим для полосы панели шириной b = 1 м = 1000 мм.

Проверим условия п. 3.40. Поперечная сила в за­делке равна:

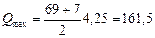кН.

Проверим условие (71), принимая h ₀ = h ₀₁ = 240 мм:

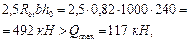
т. е. условие выполняется.

Поскольку панели связаны одна с другой, а ши­рина стенки резервуара заведомо более 5 h, значение c_max определим с учетом коэффициента a = 1,25:

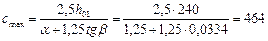мм.

Средняя интенсивность нагрузки на приопорном участке длиной c_max = 464 мм равна q ₁ = 69 – (69 – 7) 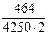= 65,6 Н/мм.

Из табл. 21 j_{b 4} =1,5.

Поскольку

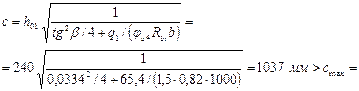
= 464 мм, принимаем с = с_max = 464 мм.

Определим рабочую высоту сечения на расстоянии от опоры (т. е. среднее значение h ₀ в преде­лах длины с):

мм.

Поперечная сила на расстоянии с == 464 мм от опоры равна:

кН.

Проверим условие (72):

кН,

т. е. прочность панели по поперечной силе обеспе­чена.

Расчет наклонных сечений

на действие изгибающего момента

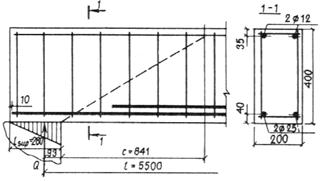
Пример 21. Дано: свободно опертая железо­бетонная балка пролетом l = 5,5 м с равномерно распределенной нагрузкой q = 29 кН/м; конструкция приопорного участка балки принята по черт. 30; бетон тяжелый класса В15 (R_b = 7,7 МПа; R_bt = 0,67 МПа при g _{b 2} = 0,9); продольная арматура без анкеров класса А-III (R_s = 365 МПа), площадью сечения A_s = 982 мм² (2 Æ 25) и 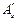= 226 мм² (2 Æ 12); хомуты из арматуры класса А-I (R_sw = 175 МПа), диаметром 6 мм, шагом s = 150 мм приварены к продольным стержням.

Требуется проверить прочность наклонных сече­ний на действие изгибающего момента.

Дата добавления: 2014-11-16