Второй способ

Первый способ

Пример

І Для уравнения 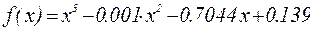найти корни на интервале [-1, 1], шаг изменения переменной х равен 0.1.

1 Записать цикл из точек интервала х:=-1, -0.9..1.

2 Записать функцию х0 =0.

3 Построить графики для этих функций.

Примечание!

Для этого на панели "Graph" выберите "X-Y Plot" (самая первая из всех кнопок на панели), и тогда у вас на экране появится область построения графика. Для того, чтобы график в ней построился, нужно в центре под осью абсцисс написать имя нашей переменной (в данном случае им будет, конечно же, x), а по центру рядом с осью ординат — имя нашей функции (то есть f(x)).

1) нажимаешь комбинацию "shift+2". Появляется окно для построения графика

2)Справа задается сама функция. Например, надо построить у(х)=4х+5. Справа пишешь имя функции, т.е. "у(х)". Если надо в одних системах координат построить несколько графиков, то нажимаешь клавишу "Б" (только не забудь включить английский язык, MathCAD работает только с ним!),это действие переводит тебя на строку ниже и там вбиваешь вторую функцию. Так можно задавать намного больше функций.

3)снизу окна задается сама переменная, т.е. в нашем случае просто "х", если у второй функции переменная с другим именем, то вторую задаешь аналогичными действиями, как и в пункте 2.

4)щелкаешь мышью в пространство MathCAD и он строит тебе график с диапазоном по умолчанию. Если тебя диапазон не устраивает, то он указан вдоль осей, там его можно поменять.

P.S. если не знаешь, как задавать функцию, то для этого примера будет прямо в MathCAD'е выглядеть так:

у(х):=4х+5

4 Определить на графике точки пересечения кривых 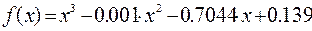и х0 =0.

Примечание!

Что ж, график у нас теперь есть. Как же определить, какая именно точка соответствует решению нашего уравнения? С этим поможет трассировка. Щелкните по получившемуся графику правой кнопкой мыши и выберите Trace. У вас на графике появится этакий "прицел", который можно будет передвигать мышкой, и окно, в котором будут отображаться координаты точки, находящейся в середине прицела (см. скриншоты). Прицел этот можно, кстати, двигать и при помощи клавиатурных стрелочек, но все равно в любом случае передвигаться он будет исключительно и только вдоль кривой, отображающей ход нашей функции, нули которой мы и ищем. Думаю, основную идею вы уже уловили: передвигая крестик-"прицел" вдоль кривой, можно в окне трассировки увидеть точку, Y-координата которой будет равна нулю.

Здесь, правда, может возникнуть небольшая проблема. В нашем уравнении, например, корень получился не целым, а трассировать функцию по X мы можем только с шагом, равным единице. Конечно, для того, чтобы локализовать корень для последующего применения функции root, в нашем случае достаточно и такой точности: достаточно найти интервал, на котором функция будет менять свой знак (то есть ее значение будет меняться с положительного на отрицательное или, напротив, с отрицательного на положительное). Но для других уравнений может случиться такое, что на единичном интервале может лежать и несколько решений — действительно, почему бы и нет, ведь даже для квадратных уравнений несложно придумать случай, когда такое может случиться. Какой из этого может быть выход? Самый простой и очевидный — уменьшить шаг трассировки по оси X, чтобы можно было более точно искать нулевые точки по оси Y. Сделать это в MathCAD очень просто. Помните, как мы задавали диапазон для нашей переменной x? Давайте кое-что поменяем и запишем его следующим образом: x:= -10,-9.9..10. Теперь уже шаг трассировки у нас будет не единица, а одна десятая (0,1). Для того, чтобы уменьшить его еще в десять раз, нужно записать x:= -10,-9.99..10. Общий принцип здесь вполне очевиден: мы записываем следующую точку диапазона следом за первой и, таким образом, указываем шаг, с которым MathCAD будет строить (а в итоге — и трассировать) наш график. Для более наглядного отображения данных имеет смысл добавить на график координатную сетку. Сделать это можно, если кликнуть по графику дважды, а затем в появившемся окне (см. скриншот) установить флажки напротив пунктов Grid Lines в категориях X Axis и Y Axis. Первый флажок устанавливает координатные линии для оси X, а второй, соответственно, для оси Y. Единственное, что также рекомендую — так это сразу поменять и цвет линий координатной сетки, кликнув по квадратикам рядом с этими пунктами — по умолчанию он задан кислотно-зеленым, что не очень удобно для глаз. Хотя это уже, конечно, дело вкуса.

5 Задать как приближение значения точек пересечения х1, х2, х3. В примере х1=-0.9, х2=0.2, х3= 0.7.

6 Вычислить значение корней с помощью формул: root (f(x1),x1), root (f(x2),x2), root (f(x3),x3). Полученные значения корней такие: х1=-0.92, х2=0.21, х3= 0.721 (рис. 18).

Рисунок 18 – Результат нахождения корней с использованием функции root

II Для уравнения 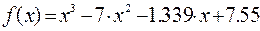найти корни на интервале [-1.1, 7.1], шаг изменения переменной х равен 0.1.

1. Создать вектор из коэффициентов уравнения, используя панель управления Matrix (Матрица) (рис.19) и задав один столбец и четыре строки для коэффициентов уравнения.

Рисунок 19 – Диалоговое окно для определения вектора из коэффициентов уравнения

Вектор из коэффициентов уравнения будет иметь следующий вид

2. С помощью встроенной функции r:= polyroots (v) найти корни уравнения и представить их в виде вектора r^T, транспонированного по отношению к r, то есть преобразованного из столбца в строку.

3. Создать циклы для переменной х и количества найденных корней:

4. Построить графики для функции и определить функцию в точках корней. В точках корней значения функции равны нулю.

5. Определить значения корней на графике (рис. 20).

Рисунок 20 – Результат нахождения корней с использованием функции polyroots

III Для уравнения 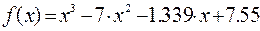найти корни с использованием символьных решений уравнений.

1. Записать левую часть уравнения

.

2. Поставить логический знак «=» и в правой части записать 0.

Примечание!

В уравнениях нельзя использовать знак равенства, взятый с кла­виатуры. Нужно использовать знак уравнения с панели инстру­ментов (= или нажать одновременно Ctrl+ =).

3. Выделить переменную х.

4. Обратиться в главном меню MathCad к команде Symbolic/Variable/ Solve.

Найдены корни уравнения запишутся в виде вектора:

IV Найти приближенное решение вышеприведенного уравнения с использованием функции minerr (x 1,…).

1. Задать приближение последовательно для первого корня х:=1.

2. Ввести ключевое слово given (дано), с которого начинается блок решений.

3. Записать уравнение, используя знак логического равенства между правой и левой частью уравнения.

4. Обратиться к функции minerr (x). Корень будет найдено.

5. Аналогические действия выполнить для двух других корней уравнения, поскольку уравнения третьей степени имеет не больше трех корней.

Контрольные вопросы

1 Какие встроенные функции позволяют находить корни уравнения?

2 Как выполняется символьное нахождение корней уравнений?

Дата добавления: 2014-11-16