Лабораторная работа №5 Нахождение решений системы линейных уравнений в MathCad

Пример

Выполнить действия с матрицами, создав их из заданных коэффициентов a=1, b=2, c= 3, m=4, k=5, n=6. Матрицы имеют следующий вид:

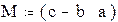
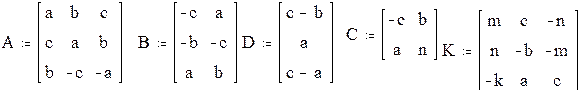
1. Создать матрицы.

1.1. Выбрать панель управления Matrіx (Матрица).

1.2. Определить число строк и столбцов для каждой матрицы (рис.21).

Рисунок 21 - Диалоговое окно для определения размера матрицы

1.3. Матрицы в примере имеют такие размеры: А - (3´3), В - (3´2), С(2´2), М(1´2), К(3´3).

1.4. Заполнить матрицы соответствующими параметрами.

2 Выполнить следующие действия с матрицами:

1) А+n·K; 2)A·B; 3) A²; 4) A·D; 5)D·M; 6) D-1.

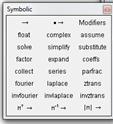
3 Найти ранг матрицы А (ранг матрицы -наибольший порядок минора этой матрицы, который отличный от нуля): rank(A).

4 В символьном виде выполнить транспонирование матрицы В, т.е. заменить местами строки и столбцы матрицы В.

4.1 Выделить матрицу В.

4.2 Обратиться в главном меню к команде Symbolіc / Matrіx/Transpose (рис. 22).

5 В символьном виде выполнить инвертирование матрицы А (т.е. найти матрицу, которая будет обратной к матрице А).

5.1 Выделить матрицу A.

5.2 Обратиться в главном меню к команде Symbolіc/Matrіx/Іnvert (рис.22).

6 В символьном виде найти обратную матрицу К.

6.1 Выделить матрицу К.

6.2 Обратиться в главном меню к команде Symbolіc / Matrіx/Іnvert (рис.22).

7 В символьном виде найти детерминант (определитель) матрицы А.

7.1 Выделить матрицу A.

7.2 Обратиться в главном меню к команде Symbolіc/Matrіx/Determіnant (рис.22).

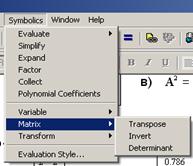
Рисунок 22 – Меню Symbolic для работы с матрицами в символьном виде

Рисунок 23 – Результаты вычисления матриц

Контрольные вопросы

1 Як можно создать матрицу и вектор?

2 Какие действия выполняются с матрицами?

3 Как определяются элементы матрицы?

Цель работы: нахождение решений системы линейных уравнений в программе MathCad.

Указания к выполнению лабораторной работы:

I Найти решение системы линейных уравнений с использованием функции soln.

1 Запустить программу MathCad.

2 Создать матрицу А из коэффициентов при неизвестных.

3 Создать вектор b из свободных членов.

4 Обратиться к встроенной программе решения линейных уравнений soln и записать soln₁:=А^-1 ×b.

5 Получить решение линейного уравнения у векторному виде

.

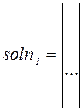II Найти решение системы линейных уравнений с использованием так званого «блоку решений».

1 Задать начальные значения переменным, которые есть в уравнении.

2 Ввести ключевое слово given (дано), с которого начинается блок решений.

3 Записать уравнение, используя знак логического равенства между правой и левой частью уравнения из панели управления Evaluation (Выражения).

4 Ввести ключевое слово find (найти), которым заканчивается блок решений.

III Найти решение вышеприведенной системы уравнений с использованием функции lsolve.

1Создать матрицу А из коэффициентов при неизвестных.

2 Создать вектор b из свободных членов.

4 Обратиться к встроенной программе решения линейных уравнений lsolve и записать lsolve(А,b).

5 Получить результат решения линейного уравнения в векторном виде

.

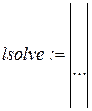IV Найти приближенное решение с использованием функции minerr (x 1,…).

1 Задать приближение последовательно для значений переменной х1, х2,… хn.

2 Ввести ключевое слово given (дано), с которого начинается блок решений.

3 Записать систему уравнений, используя знак логического равенства между правой и левой частями каждого уравнения.

4 Обратиться к функции minerr (x 1,x2,..). Значения неизвестных будут найдены.

Таблица 3.1 – Варианты заданий к лабораторной работе № 3

№ варианта	Коэффициенты при неизвестных	Свободные члени
a11 а21 а31 а41	а12 а22 а23 а24	а13 а23 а33 а34	а14 а24 а34 а44	в1 в2 в3 в4
	0,12	-0,43	0,14	0,64	-0,17
-0,07	0,34	-0,72	0,32	0,62
1,18	-0,08	-0,25	0,43	1,12
1,17	0,53	-0,84	-0,53	1,15
	0,12	-0,43	0,14	0,64	-0,17
-0,07	0,34	-0,72	0,32	0,62
1,18	-0,08	-0,25	0,43	1,12
1,17	0,53	-0,84	-0,53	1,15
	3,7	5,6	9,5
	3,36	31,1	1,5
	7,93	4,2	6,3	4,4
	42,7	3,7	6,2
	1,3	1,6		2,2
4,4	6,7		2,5
2,8	0,73		67,8
	3,4
	5,3	1,6	5,5		3,3
4,1	6,4	3,9
2,1	3,3	2,04		4,9
				3,1
				0,2
		8,3	5,3
		2,6	6,1	4,1
		0,93		3,8
					34,7
		3,6
	3,4			4,2
	44,7
			5,1	0,2
		3,4	5,34
		2,7	6,7
		3,3
				2,5	1,3
			5,2	0,78
			6,11	4,2
			6,78	3,76
				2,3
		3,4	2,5
		0,2
			1,25
		3,3	8,2
		1,2
		1,3
			5,9
	6,6
	3,3	2,1
	4,8
0,4
0,2
	1,3		1,5	2,22	3,2
		3,4	5,55	1,3
	3,3	2,2	6,77
	4,9	3,6	6,88
				0,4
				0,3
	3,3	7,6	5,5
5,4
9,2
3,2
0,44
0,67
	3,35		5,3
4,22	6,7	3,5
2,8	3,8	2,9
2,34		3,44
			5,23
	13,4	6,33	5,1	2,11	3,33
4,66	6,1	3,33	5,44	0,11
2,22		2,55	6,33	4,44
2,98		3,78	6,11	3,33

Дата добавления: 2014-11-16