К практическим занятиям

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО МАТЕМАТИКЕ

ДЛЯ СТУДЕНТОВ ФАРМАЦЕВТИЧЕСКОГО ФАКУЛЬТЕТА

2011
Тематический план лекций

(2-х часовых) по курсу «Математика»

на 1 курсе фармацевтического факультета

№ п/п	Тема
	Производная и дифференциал функции Применение производной к исследованию функции при построении графиков.
	Неопределенный интеграл. Определенный интеграл
	Решение некоторых задач физико-химического и медико-биологического содержания с применением дифференциального и интегрального исчислений
	Простейшие дифференциальные уравнения. Решение ДУ первого порядка с разделяющимися переменными. Применение ДУ в решении различных задач.
	Основы теории вероятностей. Случайные события. Случайные величины
	Элементы математической статистики. Погрешности измерений. Метод наименьших квадратов
	Дискретные и непрерывные временные ряды.

Всего: 14 часа

Тематический план практических занятий (2-х часовых)

по курсу «Математика»

на 1 курсе фармацевтического факультета

№ п/п	Тема	Кол-во часов
	Производная и дифференциал. Самостоятельная работа
	Решение задач на применение производных и дифференциала Самостоятельная работа
	Неопределенный интеграл Самостоятельная работа
	Определенный интеграл Самостоятельная работа
	Дифференциальные уравнения первого порядка Самостоятельная работа
	Решение задач на составление ДУ Самостоятельная работа
	Контрольная работа №1 по теме «дифференциальное и интегральное исчисление»
	Теория вероятностей случайных событий Самостоятельная работа
	Теория вероятностей случайных величин Самостоятельная работа
	Основы математической статистики Самостоятельная работа
	Контрольная работа №2 по «теории вероятностей и математической статистике»
	Корреляционный и регрессионный анализ Самостоятельная работа
	Дисперсионный однофакторный анализ Самостоятельная работа
	Теория погрешностей Самостоятельная работа
	Анализ временных рядов Самостоятельная работа
	Анализ временных рядов Самостоятельная работа
	Итоговое занятие (тестирование, проверка навыков решения типовых задач, зачет)

Всего: 34 часа

Методические указания №1

ТЕМА: «ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ»

Цель: освоить технику дифференцирования функции одной переменной; учиться решать задачи с использованием производной

1. ОСНОВНЫЕ ВОПРОСЫ

- задачи, приводящие к понятию производной; определение производной функции;

- механическая и геометрическая интерпретация производной;

- основные правила дифференцирования функции и производные основных элементарных функций.

- производные высших порядков; физический смысл производной вто­рого порядка;

-понятие дифференциала функции; дифференциал суммы, произведения, частного и сложной функции; инвариантность дифференциала;

- дифференциал второго порядка;

- применение производных к исследованию функций:

- нахождение интервалов возрастания и убывания функций;

- исследование функций на максимум и минимум;

- нахождение уравнения касательной к кривой графика функции в не­которой точке;

- применение дифференциала в приближенных вычислениях.

2. СОДЕРЖАНИЕ САМОСТОЯТЕЛЬНОЙ (домашней) РАБОТЫ:

– подготовить ответы на основные вопросы темы;

– выучить правила дифференцирования функции и научиться пользоваться таблицей производных;

– решить задачи из Морозова Ю.В. «Основы высшей математики и статистики», С.36,1 (нечетные примеры).

3. СОДЕРЖАНИЕ АУДИТОРНОЙ РАБОТЫ:

– решать задачи из Лобоцкой Н.Л. 6, 12–17, 18–59 на стр.54–55(по усмотрению преподавателя); из Ремизова А.Н. на стр.8–11 1.6(1–142) (по усмотрению преподавателя); из Морозова Ю.В на стр.36,1 (четные примеры); из Баврина И.И. на стр. 202 и далее

- исследовать функцию на максимум и минимум с помощью второй про­изводной; применение теории максимума и минимума функции к ре­шению задач;

- решить задачи из Лобоцкой Н.Л.: 1, 5, 61 - 70 (по усмотрению преподавателя), 72, 80, 85 - 100 (по усмотрению преподавателя) (на стр. 54 - 57), а также 18 -27 (по усмотрению преподавате­ля), 28, 35.

4. ПОЛУЧИТЬ У ПРЕПОДАВАТЕЛЯ ЗАДАНИЕ ПО СРС И ПРИСТУПИТЬ К ЕГО ВЫПОЛНЕНИЮ (срок – 4 недели)

& ЛИТЕРАТУРА: 1) Баврин И.И. «Высшая математика», гл. 5, §§ 5.1, 5.2

2) Морозов Ю.В. «Основы высшей математики и статистики», гл.2,.19–30

3) Лекция 1

Методические указания №2

ТЕМА: " РЕШЕНИЕ ЗАДАЧ НА ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ И ДИФФЕРЕНЦИАЛА".

Цель: научиться применять на практике понятия производных и дифференциала

1. ОСНОВНЫЕ ВОПРОСЫ

– исследование функции одной переменной на экстремум;

– приближенные вычисления;

2. СОДЕРЖАНИЕ САМОСТОЯТЕЛЬНОЙ (домашней) РАБОТЫ:

- подготовить ответы на основные вопросы темы;

- решить задачи:

Задача 1. Точка движется в первом квадранте по дуге окружности 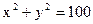так, что ордината возрастает с постоянной скоростью 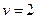. С какой скоростью изменяется абсцисса? Определить скорость изменения абсциссы в момент, когда ордината равна 6.

Задача 2. В питательную среду вносят 1000 бактерий. Численность 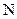бактерий возрастает согласно уравнению 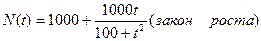, где t – время в часах. Определить максимальной количество бактерий.

Задача 3. Количество электричества (электрический заряд), протекающего через сечение проводника, определяется по формуле 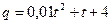(в Кл). Определите заряд, протекающий через проводник за 101– ю секунду.

3. СОДЕРЖАНИЕ АУДИТОРНОЙ РАБОТЫ:

- проверить знания основных вопросов темы;

- решать задачи из Лобоцкой Н.Л. на стр.78–79(на усмотрение преподавателя),

из Морозова Ю.В. на стр.58, Баврина И.И. на стр.366 и далее

– выполнить самостоятельную работу по теме «Дифференцирование функции одной переменной»

& ЛИТЕРАТУРА: 1. Морозов Ю.В. «Основы …», Гл.4 С.52–58

2. Баврин И.И.. «Высшая математика», Гл.7 §§7.1–7.4

3. Лекция

Методические указания №3

ТЕМА: " НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ"

Цель: овладеть простейшими приемами интегрирования функций

Дата добавления: 2014-11-16