Из последнего равенства аналогичным образом для некоторого целого неотрицательного s получаем 2 страница

4. Схема Фейстеля.

Под схемой Х. Фейстеля понимают процедуру обработки блока итеративным блочным шифром, которая не требует обратимости функции зашифрования. В общем виде схема выглядит следующим образом. Блок текста в битах (четной длины) разбивают на две равные части: левую и правую . Если предстоит совершить N раундов зашифрования, то i -й раунд выглядит так:

.

Здесь и соответственно левый и правый подблоки на i -ом шаге шифрования блока, – подключ i -го раунда, F – функция зашифрования, – операция сложения по модулю 2. Итогом работы является блок 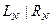. Процедура расшифрования данного блока в общем виде выглядит так:

.

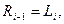
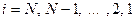В качестве функции F могут быть использованы произвольные детерминированные процедуры.

5. Общее описание DES.

Американский стандарт шифрования данных (Data Encryption Standard – DES) был принят в 1977 году. Он представляет из себя блочный симметричный алгоритм, работающий со строками длиной в 64 бита, построенный с использованием схемы шифрования Фейстеля и обрабатывающий блоки за 16 раундов. При этом используется ключ длиной в 64 бита, где 8 битов отводится для контроля четности и, таким образом, реально применяемый ключ имеет длину в 56 бит. Общая схема работы алгоритма DES выглядит так. Сначала блок текста подвергается перестановке, осуществляющей начальное перемешивание. Затем работа проходит по схеме Фейстеля. После выполнения последнего 16 раунда над блоком производится перестановка, обратная начальной.

Раундовый подключ имеет длину, равную 48 битам, который вырабатывается из 56 битного исходного ключа, записанного в два 28-битных регистра сдвига. В этих регистрах содержимое перемещается в каждом такте на количество битов, зависящее от номера раунда. Например,

номер раунда: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

сдвиг: 1 1 2 2 2 2 2 2 1 2 2 2 2 2 2 1.

Результирующая ключевая последовательность получается путем выборки 48 бит из содержимого регистров в соответствии с определенной заранее подстановкой.

Работа преобразования F происходит следующим образом. Сначала происходит расширение исходной 32 битной последовательности до 48 битной путем дописывания отдельных битов в соответствии с некоторой подстановкой. Результат расширения суммируется по модулю 2 с 48 битной ключевой последовательностью. Полученный 48 битный вектор поступает на вход S-боксов, основная задача которых заключается в том, чтобы заменить 48 битный вектор на 32 битный. В DES используется 8 S-боксов, имеющих 6 битные входы и 4 битные выходы. Подстановка в S-боксах осуществляется, например, так:

14 4 13 1 2 15 11 8 3 10 6 12 5 9 0 7

0 15 7 4 14 2 13 1 10 6 12 11 9 5 3 8

4 1 14 8 13 6 2 11 15 12 9 7 3 10 5 0

15 12 8 2 4 9 1 7 5 11 3 14 10 0 6 13

Строки пронумерованы сверху вниз от 0 до 3, а столбцы слева направо от 0 до 15. Номер строки задается первым и последним битом входа S-бокса, а номер столбца – средними четырьмя битами входа. Битовое представление содержимого ячейки S-бокса и подается на выход. В итоге с выходов 8 S-боксов снимается 32 битный вектор. Аналитическая сложность дешифрования DES зависит от математических свойств S-боксов, поскольку в них реализуются нелинейные преобразования.

Расшифровка в DES происходит аналогично зашифрованию с той лишь разницей, что выборка ключевой последовательности в раундах расшифрования будет обратная, т.е. .

К недостаткам DES относят:

1) наличие слабых ключей;

2) небольшая длина ключа (56 бит);

3) избыточность ключа (наличие дополнительных 8 бит);

4) использование статических подстановок в S-боксах.

6. Краткие сведения о ГОСТ 28147-89.

ГОСТ – симметричная блочная криптосистема, работающая с блоками в 64 бита по схеме Фейстеля с ключом в 256 бит. Процедура зашифрования и расшифрования производится за 32 раунда. Как и DES, в алгоритме ГОСТ имеются S-блоки, но они засекречены, поэтому общий объем засекреченной информации (вместе с ключом) составляет примерно 610 бит.

7. Поточные шифры.

В разделе 2 п.8 рассматривался абсолютно стойкий (по Шеннону) шифр, где операция шифрования задавалась равенством

. (3.1)

Здесь есть соответственно i -й бит открытого сообщения, ключевой последовательности и закрытого текста, а n – длина открытого текста. О неудобствах такого шифра было коротко сказано. Для того чтобы обойти указанные неудобства, было предложено использовать в качестве ключевой последовательности не случайную, а псевдослучайную последовательность, вырабатываемую генератором псевдослучайных чисел. Это решение выводит систему из класса абсолютно стойких шифров. Разве что можно надеяться на то, что для раскрытия такой системы потребуется очень много времени (например, нужно будет выполнить перебор всех начальных значений генератора). В качестве возмещения за потерю совершенности получаем возможность использовать короткие (несколько сотен бит) секретные ключи, которые гораздо проще распределять и хранить.

Шифр, построенный на основе равенства (3.1), где в качестве используется псевдослучайная последовательность, называется поточным шифром.

Как правило, исходное сообщение и ключевая последовательность представляют собой независимые потоки битов. Так как шифрующее и расшифровывающее преобразование для всех поточных шифров одно и то же, они различаются только способом построения генераторов псевдослучайных чисел. В качестве примера (на самом деле непригодного для криптографических целей) приведем следующий генератор:

,

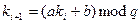где а, b, q – некоторые целые константы, а 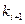– очередное псевдослучайное число, вычисляемое по предыдущему . Попробуйте выписать получающуюся последовательность для а = 5, b = 12, q = 23.

Для использования в криптографических целях генератор должен удовлетворять следующим требованиям:

1) период последовательности должен быть очень большим;

2) порождаемая последовательность должна быть «почти» неотличима от действительно случайной последовательности, в частности, вычисление числа 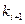по известным предыдущим элементам последовательности без знания ключа должно быть трудной вычислительной задачей (практически не решаемой).

8. Общее описание шифра RC4.

Рассмотрим один из примеров поточного шифрования. RC – сокращенно от английского Ron’s Cipher (шифр Рона). Этот шифр разработал Рон Райвест (Ron Rivest) из Массачусетского технологического института. RC4 – очень быстрый поточный шифр.

Массив S [0..255], заполненный целыми числами от 0 до 255 переставляется зависящим от ключа способом. Правило при этом следующее. На старте алгоритма

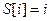.В другой массив длиной 256 байтов заносится необходимое количество копий ключа. После этого присваивается параметру j нулевое значение, и выполняются следующие шаги, последовательно увеличивая параметр i от 0 до 255:

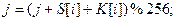// сложение по mod 2

Полученный таким образом перемешанный массив подается на вход RC4. В результате работы алгоритма получается поток ключей K, который складывается по mod 2 c открытым текстом по одному байту за один раз. Поскольку алгоритм оперирует с байтами, а не с битами, и использует наиболее простую операцию, он является быстрым и в программной реализации. Более подробно.

Сначала обнуляются переменные i и j, а затем повторяется следующая процедура:

Стойкость шифра основана на следующем наблюдении: даже если противник узнал ключ K и номер шага i, он может вычислить лишь значение , но не все внутреннее состояние массива. Это следует из того, что противник не в состоянии определить значение переменной t, не зная j, 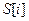или .

Каждый шаг этого алгоритма увеличивает криптостойкость.

обеспечивает использование каждого элемента массива, причем однократное;

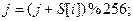обеспечивает нелинейную зависимость выходных данных от массива;

изменяет массив в процессе итераций;

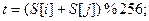из-за этого этапа генерируемая последовательность мало говорит о внутреннем состоянии массива.

RC4 может находиться в примерно возможных состояний. Здесь описана 8-битовая версия алгоритма, но она может быть трансформирована и в 16-битовую. Компания-производитель RSADSI утверждает, что продукт устойчив к дифференциальному и линейному криптоанализу (см. ниже). С длиной ключа до 40 бит имеет специальные экспортные возможности.

9. Общие методы криптоанализа.

Заметим, что разработано небольшое число довольно успешных методов нападений, применимых вообще к любому шифру. Именно

10. Дифференциальный криптоанализ. В дифференциальном криптоанализе изучаются пары шифртекстов, исходные сообщения в которых имеют специфические различия. Результат применения логической операции исключающего «ИЛИ» к таким парам называется дифференциалом. Определенные дифференциалы обладают характерными свойствами, зависящими от использованного ключа. Исследуя вероятности дифференциалов, вычисленных при атаке с выбором открытого текста, можно надеяться на выявление основной структуры ключа.

11. Линейный криптоанализ. Идея линейного криптоанализа состоит в том, чтобы аппроксимировать нелинейные компоненты шифра линейными функциями, а далее, опираясь на распределение вероятностей, получить полезную информацию о ключе.

12. Сравнительные свойства блочных и поточных шифров.

1) Блочный шифр является более общим. Его можно трансформировать в поточный.

2) Поточный шифр имеет более математизированную структуру, что с одной стороны дает больше возможностей для его взлома, а с другой – позволяет легче изучать и строго оценивать его стойкость.

3) Общие поточные шифры не очень удобны с точки зрения программного обеспечения, так как они обычно шифруют один бит за прием. Однако они высоко эффективны с точки зрения аппаратной реализации.

4) Блочные шифры удобны как для программных, так и для аппаратных средств, но они не допускают такой высокой скорости обработки информации, как поточные.

5) Аппаратные средства функционируют быстрее, чем программное обеспечение, но этот выигрыш происходит за счет снижения гибкости.

Раздел четвертый

1. Математический формализм.

1) Алфавит – любой конечный упорядоченный набор символов произвольной

природы.

2) Слово в алфавите – любой конечный упорядоченный набор символов алфавита.

3) Длина слова – количество символов алфавита в слове.

4) Обозначения: – множество слов в алфавите А, 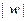– длина слова w.

Пусть – множества открытых текстов, множество шифртекстов и множество ключей соответственно, описанные в соответствующих же алфавитах (эти множества еще называют пространствами). Тогда правило зашифрования можно описать, как функцию:

или

.

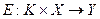Зачастую это отображение, но может быть и многозначной функцией. Введем еще обозначения: и .

Правило расшифрования опишем по аналогии:

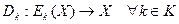
или

.

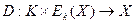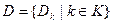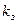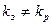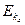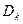И обозначим . При этом, если представляется в виде пары , где – ключ зашифрования, а – ключ расшифрования и , то понимается как , а – как 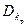. Тогда можно дать такое

Определение. Шифром (криптосистемой) называется совокупность

введенных множеств, для которых выполняются следующие требования:

1) для любых и справедливо равенство ;

2) .

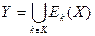Это определение задает математическую модель шифра, т.н. алгебраическую модель (в отличие от вероятностной). Первое условие в определении обеспечивает однозначность расшифровки шифртекста, а второе означает, что любой элемент 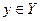может быть представлен через 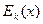для подходящих и .

Исходя из такого определения и пользуясь введенными обозначениями можно формализовать шифры простой замены и перестановки. Введем шифр простой замены в алфавите А.

Определение. Пусть 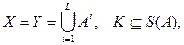где S(A) – симметрическая группа подстановок множества А. Для любого ключа , открытого текста и шифрованного текста правила зашифрования и расшифрования шифра простой замены в алфавите А определяются формулами

(*)

где – подстановка, обратная к k.

В более общей ситуации для шифра простой замены 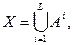причем 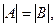а K представляет собой множество всех биекций множества А на множество В. Правила зашифрования и расшифрования определяются для (и обратной к k биекции ) формулами (*).

Определим теперь шифр перестановки.

Определение. Пусть и пусть где 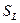– симметрическая группа подстановок множества Для любого ключа k, открытого текста и шифрованного текста 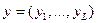правила зашифрования и расшифрования шифра перестановки определяются формулами

где – подстановка, обратная к k.

2. Алгоритмы и алгоритмические задачи.

Подходя к понятию алгоритма с точки зрения здравого смысла (не давая строгого определения) можно отметить следующие, интуитивно принимаемые, необходимые свойства, присущие этому объекту:

1) Дискретность. Алгоритм – процесс вычисления величин, идущий в дискретном времени, при котором в некоторый начальный момент времени задана исходная система величин, а в каждый последующий момент времени вычисляется новая порция величин, определяемых величинами, полученными в предыдущий момент времени.

2) Детерминированность. Система величин, получаемых в некоторый (не начальный) момент времени, однозначно определяется системой величин, полученных в предыдущий момент времени.

3) Элементарность шагов. Процедура вычисления величин в каждый отдельный момент времени должна быть простой.

4) Направленность. Если в какой-либо момент времени очередная порция величин не может быть получена, то должно быть указано, что считать результатом работы алгоритма.

5) Массовость. Алгоритм должен быть в состоянии решать потенциально бесконечное множества задач.

Рассмотрим теперь три типа алгоритмических задач, где под функцией будем понимать отображение 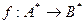; здесь А и В – произвольные алфавиты.

1) Задача вычисления функции.

Задано: .

Вычислить: f(w).

2) Задача распознавания (языка).

Пусть .

Задано: .

Распознать: ?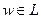

Ответ в задаче распознавания может быть закодирован битами: 1 –«да», 0 – «нет».

3) Задача поиска (элемента с заданными свойствами).

Пусть и .

Задано: .

Найти: такое, что , если такое u существует.

Здесь выражение 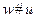означает склейку (конкатенацию) слов w, #, u.

Во всех этих задачах отдельное слово w называется индивидуальной задачей, а вся совокупность индивидуальных задач называется массовой задачей. Говорят, что алгоритм решает массовую задачу, если, приняв на вход любую индивидуальную задачу , он за конечное число шагов дает на выход ее решение. В зависимости от типа задачи говорят, что алгоритм вычисляет функцию, распознает множество или находит элемент с заданным свойством. В задаче распознавания алгоритм либо принимает вход («да»), либо отвергает вход («нет»).

Определение. Пусть t: N N – функция натурального аргумента. Говорят, что алгоритм решает массовую задачу за время t, если на каждом входе w он делает не более чем шагов.

Определение. Если алгоритм решает массовую задачу за время t, где 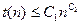для некоторых констант и , то говорят, что он решает задачу за полиномиальное от длины входа время. Такой алгоритм называется полиномиальным, а задача – полиномиально разрешимой.

Понятие полиномиального времени является основной концепцией теории сложности вычислений. Полиномиально разрешимые задачи в рамках этой концепции считаются легкими, а соответствующие алгоритмы – эффективными.

Определение. Если алгоритм на некоторой бесконечной последовательности индивидуальных задач делает более, чем шагов, где n – длина входа, а С > 0 – некоторая константа, то такой алгоритм называется экспоненциальным. Говорят, алгоритм требует экспоненциального времени, а задачу называют экспоненциально разрешимой (по крайней мере, до того момента, пока не будет найден эффективный алгоритм ее решения).

Экспоненциальные алгоритмы относят к классу неэффективных алгоритмов, а соответствующие задачи, для которых известны лишь такие алгоритмы, считаются трудными.

Следует отметить, что такая строгая классификация задач имеет, тем не менее, относительный характер, ибо зачастую экспоненциальный алгоритм работает «в среднем» вполне приемлемо, так как его зачисление в класс неэффективных алгоритмов производится из-за существования указанной «неудобной» последовательности входов. В то же время полиномиальный алгоритм может работать «долго» из-за больших значений констант .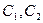

3. Некоторые задачи.

В качестве иллюстраций можно рассмотреть следующие задачи.

Задача 1. Придумать инъективное отображение 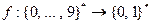, которое вычисляется быстрым алгоритмом.

Задача 2. Пусть функция, которая натуральному числу х ставит в соответствие 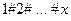– список всех натуральных чисел, не превосходящих х. Тогда

а) для и случая, когда натуральные числа записываются в двоичной системе, доказать, что любой алгоритм, вычисляющий f, должен проделать на входе длины n не меньше, чем элементарных операций (запись одного символа выхода требует по крайней мере одной элементарной операции);

б) для 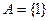и случая, когда натуральные числа задаются в унарной системе, описать алгоритм вычисления функции f, который на входе длины n делает шагов.

Задача 3. Доказать, что ни одно инъективное отображение не может быть вычислено за полиномиальное время.

Раздел пятый

1. Классификационная оценка сложности алгоритмов для арифметических задач.

В силу сложившихся традиций натуральные (и целые) числа в арифметике часто обозначаются буквой n. Учитывая тогда, что длина такого слова равна , ибо

,

где 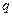– основание системы счисления, оценки для полиномиального времени и экспоненциального выглядят соответственно как

и .

2. Примеры полиномиальных алгоритмов.

1) Алгоритм Евклида.

Алгоритм Евклида есть алгоритм нахождения наибольшего общего делителя двух натуральных чисел, скажем а и b. Обозначим 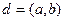. Пусть, кроме того, и . Положим . Работа на i -ом шаге алгоритма выглядит так:

,

т.е. производится операция деления с остатком. Если , то , иначе, увеличиваем i на 1 и производим новое деление с остатком.

Легко заметить, что указанный алгоритм имеет полиномиальный характер. Действительно, из неравенства 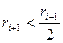следует, что остаток от деления за два шага алгоритма уменьшается более чем вдвое. Тогда, если t это число шагов, то выполняется неравенство:

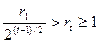для 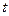нечетных и для 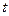четных и значит

Откуда, логарифмируя, получаем

.

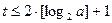Дата добавления: 2014-11-16