
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Из последнего равенства аналогичным образом для некоторого целого неотрицательного s получаем 3 страница
|
|
|
|
К сказанному добавим еще, т.н., расширенный алгоритм Евклида, который, например, позволяет решать сравнения вида  ,
,  . Добавляя к принятым обозначениям новые, имеем:
. Добавляя к принятым обозначениям новые, имеем:
 , где
, где 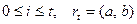 .
.
Тогда верно, что  и, значит,
и, значит, 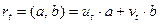 . Таким образом, для сравнения имеем:
. Таким образом, для сравнения имеем:  , т.е.
, т.е.  .
.
2) Бинарный метод.
Этот алгоритм производит возведение целого числа в натуральную степень по заданному модулю. Пусть требуется найти 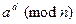 . Представим число d в системе счисления с основанием 2:
. Представим число d в системе счисления с основанием 2:
 ,
,
где  . Здесь, очевидно,
. Здесь, очевидно,  . Тогда
. Тогда
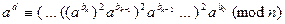 .
.
Если подсчитать количество операций умножения s, то получим оценку вида
 .
.
Ясно, что операция взятия по модулю не меняет статуса алгоритма как полиномиального. Если учитывать, что машинная арифметика предполагает в основном вычисления с битовым представлением чисел, то следует добавить при этом, что сложение и вычитание требуют  , а умножение и деление с остатком –
, а умножение и деление с остатком – 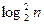 времени для чисел порядка n.
времени для чисел порядка n.
3) Вычисление символа Якоби.
Напомним свойства символа Якоби. Для 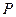 – нечетного
– нечетного
 ;
;
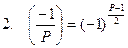 ;
;
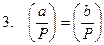 для
для 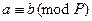 ;
;
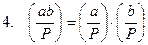 ;
;
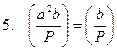 ;
;
 ;
;
 для
для 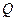 нечетного и
нечетного и 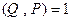 .
.
Пусть требуется вычислить значение символа Якоби  . Считаем, что
. Считаем, что 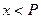 .
.
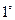 . Если
. Если 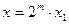 , то
, то
1) при 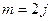
 ; иначе,
; иначе,
2) при 
 .
.
 . Если
. Если  , то
, то 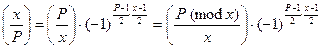 .
.
После выделения степеней 2 и «переворотов» по закону взаимности символ Якоби приводится к виду:
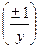 ,
,
что позволяет немедленно получить ответ. Легко видеть, что каждый «переворот» соответствует делению с остатком, как это было в алгоритме Евклида, поэтому общее число «переворотов» оценивается величиной 2 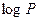 . Если добавить к этому еще вычисления с четным числителем символа и вычисление степеней -1, то оценка времени работы алгоритма будет полиномиальной, именно:
. Если добавить к этому еще вычисления с четным числителем символа и вычисление степеней -1, то оценка времени работы алгоритма будет полиномиальной, именно: 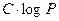 для С >2.
для С >2.
3. Вероятностные алгоритмы.
Вероятностный алгоритм отличается от детерминированного тем, что ему на вход кроме входного слова w поступает некоторая случайная последовательность 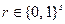 , где
, где 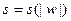 . Выход u зависит как от w, так и от r. Случайные последовательности должны выбираться с равными вероятностями
. Выход u зависит как от w, так и от r. Случайные последовательности должны выбираться с равными вероятностями  . Вероятностные алгоритмы могут давать ошибочный ответ.
. Вероятностные алгоритмы могут давать ошибочный ответ.
Говорят, что вероятностный алгоритм решает массовую задачу с вероятностью ошибки  если для любой индивидуальной задачи w он дает ее правильное решение
если для любой индивидуальной задачи w он дает ее правильное решение 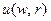 с вероятностью не меньшей, чем
с вероятностью не меньшей, чем  . Такие алгоритмы называются алгоритмами Монте-Карло. Среди этих алгоритмов различают подкласс алгоритмов типа Лас Вегас.
. Такие алгоритмы называются алгоритмами Монте-Карло. Среди этих алгоритмов различают подкласс алгоритмов типа Лас Вегас.
Говорят, что Лас-Вегас алгоритм решает массовую задачу с вероятностью неудачи  если для любой индивидуальной задачи w он дает ее правильное решение
если для любой индивидуальной задачи w он дает ее правильное решение 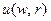 с вероятностью не меньшей, чем
с вероятностью не меньшей, чем  или выдает сообщение о невозможности решения. Последнее – с вероятностью
или выдает сообщение о невозможности решения. Последнее – с вероятностью  .
.
На вероятностные алгоритмы переносится понятие полиномиального времени. Оно оценивается на входе w, как максимальное по r время, требующееся алгоритму, работающему со словом w и использующему случайную последовательность r.
Для решения задачи распознавания выделяют еще вероятностные алгоритмы с односторонней ошибкой. Именно:
Определение. Вероятностный (Монте-Карло) алгоритм, решающий задачу распознавания языка L, называется вероятностным алгоритмом с односторонней ошибкой  если выполнены условия:
если выполнены условия:
 При
При 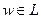 алгоритм принимает вход с вероятностью 1.
алгоритм принимает вход с вероятностью 1.
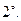 При
При  алгоритм отвергает вход с вероятностью не менее, чем
алгоритм отвергает вход с вероятностью не менее, чем  .
.
Для таких алгоритмов существует простая схема уменьшения вероятности ошибки. Эта схема реализуется следующим вероятностным алгоритмом. Пусть А – вероятностный алгоритм с односторонней ошибкой  . Тогда алгоритм В работает так:
. Тогда алгоритм В работает так:
Вход: 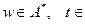 N.
N.
1) Генерируется случайная последовательность  . Эта последовательность разбивается на t равных частей
. Эта последовательность разбивается на t равных частей  так что каждая из
так что каждая из 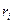 , где
, где  , является случайной последовательностью длины s.
, является случайной последовательностью длины s.
2) Моделируется работа алгоритма А на слове w с каждой из указанных случайных последовательностей 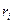 ,
,  . При этом получаются t ответов
. При этом получаются t ответов  ,
,  .
.
3) Если  , то вход принимается, иначе, вход отвергается.
, то вход принимается, иначе, вход отвергается.
Легко увидеть, что алгоритм В есть вероятностный алгоритм с односторонней ошибкой, ибо если 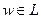 , то с вероятностью
, то с вероятностью  вход принимается, а если
вход принимается, а если  , то так как вычисления на t шагах были независимыми, то В может ошибиться с вероятностью
, то так как вычисления на t шагах были независимыми, то В может ошибиться с вероятностью 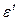 . Если положить
. Если положить  , C > 0 (т.к.
, C > 0 (т.к.  , то ошибка алгоритма В выражается величиной
, то ошибка алгоритма В выражается величиной 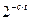 , что означает экспоненциальное понижение величины ошибки. При этом если алгоритм А был полиномиальным, то даже при полиномиальном росте t алгоритм В будет тоже полиномиальным вероятностным алгоритмом.
, что означает экспоненциальное понижение величины ошибки. При этом если алгоритм А был полиномиальным, то даже при полиномиальном росте t алгоритм В будет тоже полиномиальным вероятностным алгоритмом.
Соответствующие примеры встретятся в последующих разделах.
4. Оракульные алгоритмы.
Под оракулом понимается любая функция  . Оракульный алгоритм – это алгоритм в обычном смысле слова, но снабженный специальной функцией: обращением к оракулу. Алгоритм А, имеющий доступ к оракулу
. Оракульный алгоритм – это алгоритм в обычном смысле слова, но снабженный специальной функцией: обращением к оракулу. Алгоритм А, имеющий доступ к оракулу  , обозначим через А
, обозначим через А  . Вырабатывая некоторое слово
. Вырабатывая некоторое слово  , алгоритм обращается с запросом w к
, алгоритм обращается с запросом w к
оракулу, вычисляет значение 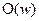 – ответ оракула – и продолжает свою работу, используя этот ответ. Один и тот же алгоритм может иметь доступ к разным оракулам. Понятие оракула весьма широкое. В терминах программистской практики обращение к оракулу можно рассматривать, как обращение к подпрограмме. Само обращение к оракулу рассматривается как один шаг алгоритма. Оракульные алгоритмы позволяют сформулировать описание сравнимости алгоритмических задач по их сложности.
– ответ оракула – и продолжает свою работу, используя этот ответ. Один и тот же алгоритм может иметь доступ к разным оракулам. Понятие оракула весьма широкое. В терминах программистской практики обращение к оракулу можно рассматривать, как обращение к подпрограмме. Само обращение к оракулу рассматривается как один шаг алгоритма. Оракульные алгоритмы позволяют сформулировать описание сравнимости алгоритмических задач по их сложности.
Определение. Говорят, что задача 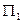 сводится к задаче
сводится к задаче 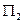 при помощи оракульного алгоритма А
при помощи оракульного алгоритма А 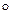 , если для любого оракула
, если для любого оракула  , который произвольную индивидуальную задачу w массовой задачи
, который произвольную индивидуальную задачу w массовой задачи 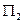 отображает в ее правильное решение, оракульный алгоритм А
отображает в ее правильное решение, оракульный алгоритм А 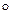 решает задачу
решает задачу 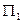 . Такой оракульный алгоритм называют сведением задачи
. Такой оракульный алгоритм называют сведением задачи 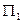 к задаче
к задаче 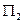 .
.
Определение. Сведение называется полиномиальным, если А 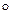 полиномиален.
полиномиален.
Определение. Если задача 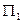 полиномиально сводится к задаче
полиномиально сводится к задаче 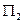 , то говорят, что задача
, то говорят, что задача 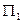 не сложнее задачи
не сложнее задачи 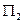 , а задача
, а задача 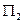 не проще, чем задача
не проще, чем задача 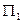 .
.
Понятие оракульного алгоритма переносится и на вероятностные алгоритмы.
Определение. Если задача 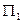 полиномиально сводится к задаче
полиномиально сводится к задаче 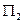 , а задача
, а задача 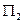 полиномиально сводится к задаче
полиномиально сводится к задаче 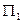 , то такие задачи называются полиномиально эквивалентными.
, то такие задачи называются полиномиально эквивалентными.
Полиномиально эквивалентные задачи рассматриваются как задачи одинаковой сложности. Примером полиномиально эквивалентных задач может служить пара 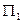 и
и 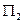 полиномиально разрешимых, где первая есть вычисление
полиномиально разрешимых, где первая есть вычисление  различных значений многочлена степени
различных значений многочлена степени 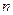 , а вторая – восстановление многочлена степени
, а вторая – восстановление многочлена степени 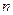 по его
по его  значениям по интерполяционной формуле Лагранжа.
значениям по интерполяционной формуле Лагранжа.
Примером полиномиально эквивалентных, но экспоненциально разрешимых на сегодняшний день задач могут служить задачи нахождения нетривиального делителя составного числа 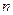 и задача факторизации числа такого числа.
и задача факторизации числа такого числа.
Раздел шестой
1. Построение больших простых чисел.
Криптографические приложения требуют больших простых чисел. Поэтому методы построения последних чрезвычайно важны. В простейшем случае дело обстоит так: надо взять некоторое натуральное число и подвергнуть его проверке на простоту, В случае, если проверка успешно пройдена, то число найдено. Таким образом, востребованными оказываются способы проверки простоты, которые называются тестами на простоту. Приведем пример простейшего теста.
Вход: 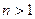 .
.
Положить  .
.
1. Если  , то продолжать. Иначе закончить с резолюцией «простое».
, то продолжать. Иначе закончить с резолюцией «простое».
2. Вычислить  .
.
3. Если  , то закончить с резолюцией «составное».
, то закончить с резолюцией «составное».
4. Если 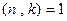 , то увеличить k на единицу и вернуться к выполнению п.1.
, то увеличить k на единицу и вернуться к выполнению п.1.
Ясно, что в случае, когда число n составное, процесс проверки может закончиться очень быстро. Например, если n – четное или кратно какому-либо малому простому числу. Но если n – число простое, то придется сделать  шагов. Конечно, границу для k в п.1 можно уменьшить до
шагов. Конечно, границу для k в п.1 можно уменьшить до  , руководствуясь известным результатом из элементарной арифметики.
, руководствуясь известным результатом из элементарной арифметики.
Наименьший простой делитель составного числа n не превосходит 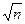 .
.
Но и тогда алгоритм остается экспоненциальным, т.е. время его работы может составить 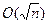 .
.
Другим известным способом определения простоты числа является решето Эратосфена (около 250 г. до н. э.). Этот алгоритм позволяет на основе указанного выше результата получить список всех простых чисел  , еслирасполагать подобным списком для простых
, еслирасполагать подобным списком для простых  . Для своей реализации на ЭВМ этот метод требует очень большого объема памяти, а время его работы можно оценить величиной
. Для своей реализации на ЭВМ этот метод требует очень большого объема памяти, а время его работы можно оценить величиной  . Оба метода работают очень медленно, и для нужд криптографии неприменимы.
. Оба метода работают очень медленно, и для нужд криптографии неприменимы.
До последнего времени (2002 г.) неизвестны были детерминированные полиномиальные тесты на простоту. Лучший из апробированных тестов Адлемана-Румли (с улучшениями от Ленстры) являлся квазиполиномиальным, ибо его время работы оценивается величиной
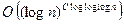 ,
,  .
.
Этот алгоритм способен различать простые числа порядка  и выше за приемлемое время. Таким образом, несмотря на существенный прогресс, достигнутый не так давно в деле тестирования простоты, цель получения полиномиального теста оставалась все же недосягаемой. Но группой индийских математиков (M. Aгравал, Н. Kайал и Н. Саксена) в 2002 г. неожиданно был предложен полиномиальный детерминированный тест простоты. Упомянутый алгоритм работает за время
и выше за приемлемое время. Таким образом, несмотря на существенный прогресс, достигнутый не так давно в деле тестирования простоты, цель получения полиномиального теста оставалась все же недосягаемой. Но группой индийских математиков (M. Aгравал, Н. Kайал и Н. Саксена) в 2002 г. неожиданно был предложен полиномиальный детерминированный тест простоты. Упомянутый алгоритм работает за время 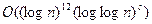 ,
,  если число n – простое. Показатель степени в оценке времени работы достаточно велик, чтобы тест считать удобным для применения, Дальнейшие усовершенствования алгоритма Агравала, Кайала и Саксены были предложены Х. Ленстрой, К. Померансом и Д. Бернштейном. Им удалось понизить оценку сложности до
если число n – простое. Показатель степени в оценке времени работы достаточно велик, чтобы тест считать удобным для применения, Дальнейшие усовершенствования алгоритма Агравала, Кайала и Саксены были предложены Х. Ленстрой, К. Померансом и Д. Бернштейном. Им удалось понизить оценку сложности до 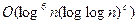 битовых операций. Иное дело – вероятностные тесты простоты.
битовых операций. Иное дело – вероятностные тесты простоты.
2. Псевдопростые числа и вероятностные тесты на простоту.
Определение. Пусть n – нечетное составное число и пусть b – любое целое такое, что  . Тогда n называется псевдопростым Ферма, или просто псевдопростым, по основанию b, если выполняется сравнение
. Тогда n называется псевдопростым Ферма, или просто псевдопростым, по основанию b, если выполняется сравнение
b 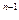
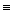 1 (mod n). (6.1)
1 (mod n). (6.1)
Пример. Число n = 91 является псевдопростым по основанию 3, так как справедливо сравнение: 3 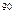
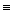 1 (mod 91). Однако 91 не является псевдопростым по основанию 2, ибо 2
1 (mod 91). Однако 91 не является псевдопростым по основанию 2, ибо 2 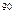
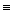 64 (mod 91). Если не знать, что 91 есть составное число, то последнее сравнение убеждает в этом (
64 (mod 91). Если не знать, что 91 есть составное число, то последнее сравнение убеждает в этом (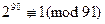 ).
).
Из определения псевдопростого числа видно, что оно в определенном смысле похоже на простое. Именно, для простых n соотношение (6.1) выполняется всегда в силу известной малой теоремы Ферма. Эта теорема могла бы служить основанием для теста на простоту, если бы не «мешали» псевдопростые. Имеет место следующая теорема.
Теорема. Существует бесконечно много псевдопростых чисел Ферма для любого основания b.
Определение. Числом Кармайкла называется нечетное составное число n, для которого сравнение (6.1) выполняется для любого числа b  Z
Z 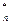 .
.
Пример.Число n = 561 = 3  11
11  17 есть число Кармайкла. Можно показать, что это есть наименьшее число Кармайкла.
17 есть число Кармайкла. Можно показать, что это есть наименьшее число Кармайкла.
Пример.Числами Кармайкла, меньшими 100000, являются: 561, 1105, 1729, 2465, 2821, 6601, 8911, 10585, 15841, 29341, 41041, 46657, 52633, 62745, 63973 и 75361.
Замечание. Недавно (1992 г.) было доказано, что множество чисел Кармайкла бесконечно.
Определение. Если n – нечетное составное число и b – такое целое число, что  и выполняется сравнение
и выполняется сравнение
b 
 (mod n), (6.2)
(mod n), (6.2)
то n называется псевдопростым числом Эйлера по основанию b.
Теорема. Если n есть псевдопростое число Эйлера по основанию b, то оно является псевдопростым Ферма по основанию b.
Доказательство. Достаточно возвести в квадрат обе части сравнения (6.2).
Пример.Утверждение, обратное теореме, неверно. В примере число 91 было псевдопростым по основанию 3. Однако,
3  27 (mod 91)
27 (mod 91)
и, значит, (6.2) не выполняется для n = 91, b = 3. Примером основания, по которому 91 является псевдопростым Эйлера, есть 10. Действительно, 10  (mod 91) и
(mod 91) и
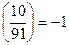 .
.
Отметим, что для псевдопростых Эйлера нет аналога чисел Кармайкла. Каждое составное число n не выдерживает тест (6.2) для по крайней мере половины всех возможных оснований b. Точнее, имеет место
Теорема. Для нечетного n  3 положим
3 положим
S 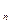 =
=  ( Z
( Z 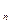 )* |
)* | 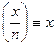
 (mod n)
(mod n) 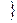 .
.
Если n составное, то |S 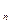 |
| 
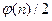 , где
, где 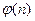 – функция Эйлера.
– функция Эйлера.
Доказательство. По мультипликативности символа Якоби S 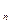 является подгруппой мультипликативной группы Z
является подгруппой мультипликативной группы Z 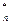 . Чтобы доказать теорему, достаточно проверить, что эта подгруппа собственная. Действительно, по теореме Лагранжа |S
. Чтобы доказать теорему, достаточно проверить, что эта подгруппа собственная. Действительно, по теореме Лагранжа |S 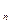 | делит | Z
| делит | Z 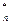 | =
| =  (n), а поэтому, если эти числа не равны между собой, то |S
(n), а поэтому, если эти числа не равны между собой, то |S 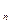 | может быть не более
| может быть не более  (n) / 2. Таким образом, остается доказать, что существует элемент у
(n) / 2. Таким образом, остается доказать, что существует элемент у  (Z
(Z 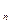 )* \ S
)* \ S 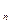 .
.
Предположим для начала, что n свободно от квадратов, т.е. в разложении n = p  … p
… p 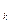 на простые множители каждое число
на простые множители каждое число  встречается лишь один раз. Выберем в Z
встречается лишь один раз. Выберем в Z 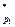 квадратичный невычет s по модулю р
квадратичный невычет s по модулю р  . По китайской теореме об остатках в Z
. По китайской теореме об остатках в Z 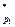 существует у такое, что
существует у такое, что
у 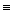 s (mod p
s (mod p  ), y
), y 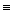 1 (mod p
1 (mod p  … p
… p 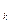 ). (6.3)
). (6.3)
Для такого у имеем
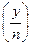 =
= 
 =
= 
 = (-1)1 = - 1.
= (-1)1 = - 1.
Но у 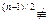 – 1 (mod n), так как было бы у
– 1 (mod n), так как было бы у 
 - 1 (mod p
- 1 (mod p  … p
… p 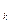 ) в противоречие с условиями (6.3).
) в противоречие с условиями (6.3).
Теперь предположим, что существует простое р такое, что р  | n. Выберем элемент у = 1+ n / p. Ясно, что для каждого простого делителя q числа n выполняется сравнение
| n. Выберем элемент у = 1+ n / p. Ясно, что для каждого простого делителя q числа n выполняется сравнение 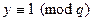 . Это означает, что у
. Это означает, что у  Z
Z 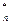 и вследствие мультипликативности символа Якоби
и вследствие мультипликативности символа Якоби
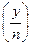 = 1.
= 1.
|
|
|
|
|
Дата добавления: 2014-11-16; Просмотров: 658; Нарушение авторских прав?; Мы поможем в написании вашей работы!