Рассмотрим русскоязычный пример

Проблема защиты информации существует с тех пор, как человек научился использовать ее в собственных целях. Приемы и методы были самыми разнообразными. Их разработка стимулировалась потребностями дипломатии, военной деятельности и, не в последнюю очередь, финансовой и коммерческой деятельности. В современном информатизированном мире, когда человек вынужден многое доверять компьютерам (совершать электронные платежи, покупать авиабилеты через специальную систему, решать какие-то деловые вопросы или интересоваться некоторой информацией, например, через Интернет и т.д.), даже не будучи связанным с военными и прочими государственными или коммерческими секретами, может сложиться ситуация, в которой возможны нарушения прав и свобод личности, если не обеспечена надлежащая защита его информационных интересов.

Криптография – это один из возможных способов защиты информации. Ее методы используются издавна, а сейчас она переживает период бурного развития, в частности, из-за ее приложений в общественной и экономической жизни. Будучи долгое время наукой, которой интересовались, прежде всего, спецслужбы, она частично вышла из тени и активно используется вне рамок тайной деятельности государственных органов.

В настоящем методическом пособии излагаются кратко основные сведения о некоторых криптографических системах вместе с небольшим количеством учебных задач, призванных обеспечить усвоение студентами основных алгоритмов, относящихся к этим системам. Отметим, что основная часть задач, хотя и носит учебный характер, вряд ли может быть решена без использования персонального компьютера или другого, сравнимого с первым, вычислительного устройства. Предполагается, что студент, получивший для решения задачу (на расшифровку текста), предпримет действия для программной реализации необходимых алгоритмов с целью поиска решения.

Основной материал излагается в курсе «Криптология». Он содержит, в частности, сведения об арифметической основе стойкости шифрующих алгоритмов, а также описание методов разрешения вопросов, возникающих в предложенных задачах. Считается, что студенты знакомы с основным содержание указанного курса. Ввиду малой величины арифметических модулей, задача факторизации целого числа, а также задача дискретного логарифмирования могут решаться применением экспоненциальных алгоритмов.

Методическое пособие не предполагает получения коммерческой выгоды и представляет собой в значительной степени компиляцию материалов, взятых из источников, отмеченных в списке литературы. Это касается как теоретического материала, так и некоторых задач. Например, раздел семнадцатый полностью взят из книги [5]. Способ изложения опирается на источник [2]. При этом список литературы носит расширенный характер.

Литература

1. Алферов А.П. и др. Основы криптографии. М.: Гелиос АРВ, 2001.

2. Вербіцький О.В. Вступ до криптології. Львів: вид. наук.-техн. літ., 1998.

3. Коблиц Н. Курс теории чисел и криптографии. М.: ТВП, 2001.

4. Молдовян А.А. и др. Криптография. СПб.: Лань, 2000.

5. Смарт Н. Криптография. М.: Техносфера, 2006.

6. Ященко В.В. и др. Введение в криптографию. СПБ.: МЦНМО Питер, 2001.

Дополнительная литература

7. Иванов М.А. Криптография, М.: Кудиц-образ, 2001.

8. Шнайер Б. Прикладная криптография. М.: Триумф, 2002.

9. Саломаа А. Криптография с открытым ключом. М.: Мир, 1995.

10. Тилборг Х.К.А. Основы криптологии. М.: Мир, 2006.

11. Лидл Р., Нидеррайтер Г. Конечные поля. М.: Мир, т.1, 1988.

Раздел первый

1. Проблема защиты информации и современные информационные технологии.

Защита информации появляется вместе с понятием тайны. Признаками тайны можно считать следующие:

1) существует круг лиц, которые обладают некоторой информацией, существующей в виде каких-то данных, или имеющих доступ к ней;

2) существует круг лиц, для которых данная информация недоступна или должна быть недоступна.

Защищать тайну можно различными способами, начиная с разного рода ловушек для ее нелегитимных искателей и до специальной технической и вооруженной охраны. Для простоты рассуждений будем говорить о текстовой информации, хотя защищать приходится и компьютерную, и телефонную, и графическую и т.п. информацию. Но как выяснилось, лучшим способом сохранения секрета есть специальное ее преобразование, приводящее к невозможности с ее ознакомлением для непосвященных. Такие преобразования носят название криптографических. Слово «криптография» в переводе с греческого буквально означает «тайнопись». В связи с широким распространением электронных информационных сетей роль криптографической защиты особенно возросла. Коммерциализация самого рынка информационных услуг привела к необходимости широкого внедрения разного рода криптографических приемов даже не связанных с собственно конфиденциальностью информационных сообщений. Отсюда вырос целый класс защитных средств криптографического характера, контролируемых, правда, соответствующими государственными структурами.

2. Криптология – наука, состоящая из двух ветвей: криптография + криптоанализ.

Криптографию можно определить как науку о способах шифрования информации, т.е. специальном ее преобразовании, затрудняющем ознакомление с ее содержанием и ее использование нелегитимными участниками информационного обмена. Более полно можно представить криптографию через описание задач, которые она призвана решать:

1) обеспечение конфиденциальности информации;

2) обеспечение целостности и достоверности информации;

3) обеспечение неотслеживаемости действий участников информационного обмена.

Криптоанализ – область деятельности в известном смысле противоположная деятельности криптографов, решающих указанные три задачи, т.е. она предусматривает разработку методов вскрытия шифров, разрушения криптографической защиты.

3. Составными частями криптографической деятельности являются:

1) разработка и анализ одноключевых (симметричных) криптосистем;

2) разработка и анализ двухключевых (асимметричных) криптосистем;

3) разработка и анализ криптографических протоколов;

4) управление ключевой информацией.

4. Введем в обращение словарь необходимых для дальнейшего изложения терминов.

Алфавит – конечный упорядоченный набор символов произвольной природы, предназначенный для записи текстовой информации.

Открытый текст – упорядоченный набор символов алфавита, предназначенный для криптографического преобразования.

Закрытый текст (шифртекст, криптотекст, криптограмма) – результат работы криптографического алгоритма, примененного к некоторому открытому тексту.

Шифр – совокупность обратимых преобразований множества открытых текстов во множество закрытых текстов, заданных алгоритмом криптографического преобразования.

Ключ – сменный элемент шифра, применяемый для закрытия отдельного сообщения, т.е. конкретное секретное состояние параметров алгоритма криптографического преобразования, обеспечивающее выбор одного из вариантов совокупности возможных преобразований. Ключом определяется в первую очередь безопасность защищаемой информации.

Шифрование (зашифрование) – преобразование открытого текста в закрытый с помощью определенных правил, содержащихся в шифре.

Расшифрование – преобразование закрытого текста в открытый, доступный для ознакомления с его содержимым (термин «дешифрование» относят к действиям противника).

Криптосистема – криптографический объект, решающий первую задачу криптографии и состоящий из пространства ключей, пространства открытых текстов, пространства закрытых текстов и алгоритмов зашифрования и расшифрования.

Раскрытие криптоалгоритма (шифра, слом системы) – результат работы криптоаналитика, приводящий к возможности эффективного определения любого открытого текста из закрытого с помощью данного алгоритма.

Криптоаналитическая атака – попытка вскрытия шифра или ознакомления с содержимым зашифрованного сообщения, как правило, незаконным пользователем (противником). Возможны криптоатаки исследовательского характера.

Стойкость криптографического объекта (криптосистемы, криптопротокола) есть его способность противостоять усилиям криптоаналитика по его разрушению (полному или частичному), т.е. противостоять криптоатакам на него.

5. Классическая криптографическая схема предполагает наличие двух легитимных участников конфиденциального обмена информацией (условно это Алиса и Боб), а также их противника, в отношении которого можно считать, что он способен перехватывать информационные сообщения, которыми обмениваются Алиса и Боб, и, возможно, вмешиваться в их информационный обмен.

А канал связи Б

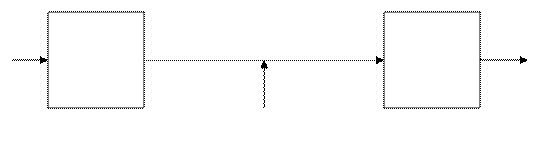
шифрующее устройство П устройство расшифровки

Алисы Е противник Боба D

Открытое сообщение Алисы М поступает в устройство Е, которое преобразует его в закрытый текст С, т.е. С = Е(М). Сообщение С передается по каналу связи, прослушиваемым возможно противником, и попадает в устройство расшифровки Боба D, которое позволяет из С восстановить М, т.е. М = D(C). В дальнейшем считаем, что действия противника носят пассивный характер, т.е. он только перехватывает зашифрованные сообщения и пытается их дешифровать.

6. Современная криптография исповедует принцип Керкгоффса, состоящий в том,

что стойкость криптообъекта должна обеспечиваться лишь секретностью ключа, в то время как иная информация о криптообъекте или информационном обмене может быть доступна противнику. Это может быть язык сообщения, форматы сообщений, тематика сообщений, используемый шифр и т.п.

7. В соответствии с принципом Керкгоффса противник может решиться на прямой перебор по всему ключевому пространству, откуда сразу следует, что это пространство должно быть большим. Такой способ действий противника носит название прямой, или грубой, атаки. Существует классификация криптоаналитических атак, различающихся по степени их силы, каковая зависит от возможностей противника:

1) атака с известным шифртекстом –

противник располагает некоторым набором перехваченных шифртекстов;

2) атака с известным открытым текстом –

противник располагает некоторым набором открытых текстов и соответст-

вующим ему набором шифртекстов;

3) простая атака с выбором открытого текста –

противник располагает возможностью для выбранных по своему усмотре-

нию открытых текстов получить соответствующие им шифртексты;

4) адаптивная атака с выбором открытого текста –

противник в условиях предыдущей атаки располагает возможностью пода-

вать на зашифрование открытые тексты порциями таким образом, что оче-

редная порция выбирается с учетом анализа зашифрования предыдущих

порций;

5) простая атака с выбором шифртекста –

противник имеет возможность подать на расшифрование выбранные по

своему усмотрению шифртексты;

6) адаптивная атака с выбором шифртекста –

противник в условиях предыдущей атаки имеет возможность подавать на

расшифрование криптотексты порциями так, что очередная порция выбира-

ется в зависимости от итогов расшифрования предыдущих порций;

7) атака с выбором текста –

противник располагает возможностями подавать на зашифрование и рас-

шифрование любые открытые и закрытые тексты;

8) атака с выбором ключа –

противник, не зная конкретных используемых ключей, знает некоторые

различия между ними.

8. Методы оценки криптоалгоритмов.

К методам оценки криптоалгоритмов относят следующие:

1) всевозможные попытки вскрытия шифра;

2) оценка сложности алгоритмов дешифрования;

3) оценка статистической безопасности шифра.

К необходим условиям стойкости криптосистемы относят следующие:

1) отсутствие статистической зависимости между входной и выходной после-

довательностями;

2) выходная последовательность должна по своим статистическим свойствам

быть похожа на истинно случайную последовательность;

3) при неизменной входной последовательности незначительное изменение

ключа должно приводить к существенному изменению выходной последо-

вательности;

4) при неизменном ключе незначительное изменение входной последователь-

ности должно приводить к существенному изменению выходной последо-

вательности;

5) отсутствие зависимости между ключами, последовательно используемыми

в процессе шифрования.

9. Стойкость шифра.

К. Шеннон ввел понятие совершенного, или абсолютно стойкого шифра, и строго доказал его существование в определенных условиях. Это шифр, который в принципе невозможно вскрыть. Основной смысл рассуждений К. Шеннона сводится к тому, что если опытом считать перехват противником шифрованного сообщения, то апостериорные вероятности открытых текстов не должны в случае такого совершенного шифра соответственно отличаться от их априорных вероятностей. Это означает, что противник в результате перехвата не получает никакой информации о сообщении, которой он не имел до перехвата (за исключением, возможно, его длины).

Пусть, например, перехвачено сообщение , где М – открытое сообщение, а Е – шифрующее отображение. Если воспользоваться формулой Байеса, то можно записать:

,

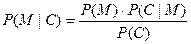где

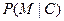– апостериорная вероятность сообщения М, при условии, что перехвачено криптограмма С;

Р (М) – априорная вероятность сообщения М;

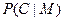– условная вероятность криптограммы С, при условии, что для отправления выбрано сообщение М;

– вероятность получения криптограммы С.

Для совершенного шифра, как указано выше, должны совпадать величины 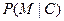и для всех М и С. Отсюда следует, что либо (что неприемлемо, ибо равенство должно выполняться для любых значений ), либо

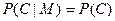
для любых М и С. Легко видеть, что верно и обратное. Таким образом, справедлива

Теорема (Шеннон К .). Необходимое и достаточное условие совершенности шифра состоит в том, что

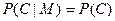
для всех М и С, т.е. 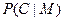не должно зависеть от М.

Иными словами, полная вероятность всех ключей, преобразующих данное сообщение 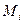в криптограмму С, равна полной вероятности всех ключей, преобразующих сообщение в ту же криптограмму С для всех 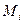, и С.

Можно показать, что условиями совершенного шифра являются следующие:

1) ключ выбирается случайно и равновероятно из ключевого пространства;

2) размер ключа должен быть равен длине сообщения;

3) ключ используется для шифрования лишь одного сообщения.

Нарушение любого из этих условий лишает шифр его статуса абсолютно стойкого

шифра.

В отличие от абсолютно стойких шифров все прочие являются стойкими в вычислительном смысле, т.е. могут быть вскрыты при выполнении определенного (как правило, очень большого) объема вычислений. Поэтому необходимые значения параметров безопасности шифра должны быть приняты такими, чтобы вероятный противник был не в состоянии такой объем вычислений выполнить за приемлемое для него время. Поэтому, заметим, что целью криптографа, создающего новый криптоалгоритм, является достижение положения, при котором противнику не остается ничего лучшего, как прибегать к прямой атаке на алгоритм.

Важную роль в изучении секретных систем передачи информации К. Шеннон уделял понятию избыточности естественных языков. Смысл этого понятия состоит в том, что обычные языки обладают свойством использовать избыточное количество символов для передачи смыслового содержания сообщения. Можно привести примеры, когда удаление значительного количества знаков алфавита из сообщения практически не влияет на смысловое содержание текста. При передаче секретной информации избыточность, если она переносится в шифртекст, может помочь противнику добраться до его содержания. По Шеннону стойкими являются те системы, которые стирают имеющуюся избыточность в открытом тексте.

Наконец, отметим еще одно важное понятие как расстояние единственности, которое можно трактовать как наименьшую длину открытого текста, для которого криптоаналитическая задача имеет единственное решение.

10. Каждая конфиденциальная информация имеет свое время тайной жизни, по истечении которого сохранение тайны становится бессмысленным. Это физическое время может располагаться в промежутке от нескольких часов до десятков и более лет. Следовательно, лицо, желающее добраться до секретной информации, должно учитывать временной фактор и не тратить свои ресурсы, если ожидаемое время, требующееся на то, чтобы добраться до тайны, превышает время ее тайной жизни. Другой стороной, тоже связанной с тратой ресурсов на добывание секретной информации, является ценность последней. Может получиться, что потраченные ресурсы превышают дивиденды, полученные от использования расшифрованной информации. Наконец, заметим, что важным фактором, влияющим на решение о трате средств на защиту, является адекватная оценка возможностей противника, от которого и требуется защита. Сильный противник, каким может выступать государство или мощная спецслужба, естественно требует и более серьезных защитных мероприятий. Таким образом, приходим к выводу, что

1) защищающейся стороне требуется оценить стоимость защиты, требующейся в условиях наличия конкретного противника, время жизни секретной информации и ее относительную ценность;

2) нападающая сторона должна учитывать ценность добываемой информации по отношению к стоимости атаки, а также временной фактор.

11. В 1976 году (по некоторым данным несколько раньше) В. Диффи и М. Хеллманом (W. Diffie, M. Hellmann) была предложена идея криптосистем с т.н. открытым ключом. Существо идеи состоит в том, что часть ключевой информации, именно та, что отвечает за процедуру зашифрования, оказывается общедоступной, в то время как ключи расшифрования сохраняются в тайне. При этом неизвестны эффективные алгоритмы, которые бы позволяли определять секретные ключи из открытых. Точнее, такое определение требовало бы решения сложной в вычислительном смысле математической задачи.

Таким образом, данные системы оказываются стойкими в вычислительном смысле. Несимметричность присутствия секретной и несекретной частей ключевой информации позволила назвать соответствующую область криптографии асимметричной криптографией, или криптографией с открытым ключом, в отличие от симметричной криптографии, где вся ключевая информация должна держаться в тайне. В последних системах один и тот же ключ может использоваться как для процедуры зашифрования, так и для процедуры расшифрования. Но если используются разные ключи, то, как правило, один определяется из другого эффективным алгоритмом.

12. В соответствии с принципом Керкгоффса ключевая информация является определяющим звеном в системе криптографической защиты. Поэтому оказывается очень важным правильное обращение с таковой. Порядок использования любой криптосистемы определяется системами установки и управления ключами. Система установки ключей определяет алгоритмы и процедуры генерации, распределения, передачи и проверки ключей. Система управления ключами определяет порядок использования, смены, хранения и архивирования, резервного копирования и восстановления, замены или изъятия из обращения скомпрометированных, а также уничтожение старых ключей.

13. Важнейшей областью современной криптографии является та ее часть, которая занимается т.н. криптографическими протоколами. Говоря неформально, под таким протоколом понимают некоторый набор правил поведения, который принимают на себя участники протокола, с целью достижения определенной цели, причем в процессе исполнения его производится криптографическое преобразование информации. Одними из наиболее востребованных протоколов является протокол цифровой подписи (ЦП). Используя средства такого протокола, отправитель сообщения доказывает адресату, что указанное сообщение пришло именно от того лица, которое его подписало. Но существует целый ряд и других прикладных протоколов. Например, протоколы разделения секрета, протоколы аутентификации, протоколы жеребьевки, протоколы голосования и т.д.

Раздел второй

1. Исторические шифры.

1) Шифр Цезаря и шифр Августа.

Текст на латинском языке изменялся за счет замены каждой буквы на третью от нее в алфавите (шифр Цезаря) или на следующую в алфавите (шифр Августа). Замена была циклической, т.е. последние буквы алфавита заменялись первыми. Это пример шифров простой замены, при которой алфавит открытых текста инъективно отображается в алфавит закрытых текстов. Ключом к шифру является величина «сдвига». Ввиду незначительной величины ключевого пространства такой шифр легко вскрывается прямой атакой. Приведем пример. Открытый текст «CAESAR» по указанному правилу Цезаря преобразуется в шифртекст «FDHVDU».

2) Шифр Сцитала (Scitale).

Открытый текст записывался на узкой полоске папируса, намотанной на деревянный цилиндр (scitale) без просветов вдоль оси цилиндра. В размотанном состоянии на ленте возникала перестановка букв текста, затрудняющая его чтение. Для расшифровки требовалась еще одна scitale у адресата, который должен был намотать на нее полученную ленту. Это пример шифра перестановки, при котором символы открытого текста переставляются в некотором порядке, определяемым ключом шифра. Ключом шифра является диаметр scitale. Аристотелю приписывается метод криптоанализа такого шифра. Следует изготовить длинный конус, на узкую часть которого наматывается лента с сообщением. Постепенно сдвигая ленту к более широкой части конуса можно надеяться, что появятся осмысленные части сообщения в месте, где диаметр поперечного сечения конуса близок к диаметру scitale. После чего можно изготовить цилиндр найденного диаметра и прочитать сообщение полностью.

3) Квадрат Полибия (древняя Греция)

В квадрат , строки и столбцы которого пронумерованы от 1 до 5, вписывались буквы латинского или греческого алфавитов по одной в каждую клетку. Латинские буквы i и j записывались в одну клетку. Шифрование производилось заменой каждой буквы открытого текста парой чисел – координат этой буквы в указанном квадрате. Это тоже шифр простой замены, но алфавит открытых текстов отличается от алфавита закрытых. Алфавит закрытого текста будет . Ключом является порядок размещения букв в квадрате. Ключевое пространство весьма обширно и оценивается величиной 25! (Сравним с числом 25 в шифрах Цезаря-Августа). Приведем пример. Зададим ключ в виде:

	A	B	C	D	E
	F	G	H	I,J	K
	L	M	N	O	P
	Q	R	S	T	U
	V	W	X	Y	Z

Тогда открытый текст «REMEMBER» преобразуется в шифртекст «4215321532121542».

4) Шифр четырех квадратов.

Латинский алфавит, из которого изъята буква j, записывается в квадрат в произвольном порядке. Составляются четыре таких квадрата, вообще говоря, различных. Квадраты записываются в матрицу 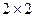так, чтобы строки и столбцы их были выровнены и составляли единое целое. Открытый текст разбивается на биграммы, т.е. пары букв. Каждая биграмма открытого текста заменяется иной биграммой по следующему правилу. Первая буква заменяемой биграммы ищется в левом верхнем квадрате, а вторая – в правом нижнем. Отмеченные буквы задают в матрице алфавитов две противоположные вершины прямоугольника. Замещающие буквы находят в вершинах этого прямоугольника соответственно в правом верхнем и левом нижнем квадрате. Этот шифр является биграммным шифром замены. Ключом служат указанные квадраты алфавитов. Объем ключевого пространства оценивается величиной 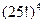. Рассмотрим пример со следующим ключом:

K	I	N	G	D		V	Q	E	O	K
O	M	A	B	C		W	R	F	M	I
E	F	H	L	P		X	S	H	A	N
Q	R	S	T	U		Y	T	L	B	G
V	W	X	Y	Z		Z	U	P	C	D
Z	Y	X	W	V		D	C	P	U	Z
U	T	S	R	Q		G	B	L	T	Y
P	L	H	F	E		N	A	H	S	X
C	B	A	M	O		I	M	F	R	W
D	G	N	I	K		K	O	E	Q	V

Расшифруйте закрытый текст «MOPWTIOMFXNS».

5) Шифр Кардано.

Шифр перестановки, которая перемешивает символы открытого текста при помощи вращения специальной маски с прорезями в установленных местах. Маска представляет собой квадрат 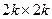, в котором сделаны вырезов таким образом, чтобы при последовательных поворотах маски на 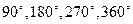вокруг центра квадрата вырезы покрывали бы его площадь без повторений. Записывая открытый текст в свободные прорези, начиная сверху и двигаясь слева направо вниз, заполняют текстом квадрат такого же размера, поворачивая маску всякий раз, как окажутся заполненными свободные места в прорезях. Затем текст считывается в одну строку из заполненного квадрата и разбивается на m-граммы. Ключом является маска. Ключевое пространство оценивается величиной 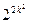. Рассмотрим пример. Пусть ключ имеет вид, где темные квадраты означают прорези:

Для k = 2 зашифруем фразу: «ПО ПРОЧТЕНИИ СЖЕЧЬ». В соответствии с алгоритмом шифрования лишаем текст пробелов и вписываем буквы в имеющиеся прорези, изображенные жирными линиями. Получим до первого поворота

			П
		О
П
	Р

Далее, поворачивая маску по часовой стрелке вокруг центра квадрата на угол , продолжаем вписывать буквы открытого текста в прорези, начиная сверху. Затем вновь поворачиваем на и т.д. Когда вписывание закончено, получим:

Ж	О	Н	П
Ч	Е	О	И
П	И	Т	Ч
С	Р	Ь	Е

Считывая текст построчно, разобьем его на блоки: «ЖОНПЧЕОИ ПИТЧСРЬЕ».

6) Шифр ADFGVX.

Немецкий военный шифр времен первой мировой войны, представляющий собой композицию двух шифров: билитеральной замены и матричного шифра обхода. Тридцать шесть символов открытого текста (26 латинских букв и 10 цифр) записываются в матрицу , строки и столбцы которой, как в квадрате Полибия, пронумерованы буквами, вынесенными в заголовок. Открытый текст на латинице, который лишается пробелов и знаков препинания, но может содержать цифры, преобразуется билитеральной заменой, т.е. каждый символ текста заменяется парой буквенных координат. Затем полученный текст подвергается повторному шифрованию, при котором он выписывается под заранее задуманным словом-лозунгом буква под буквой так, что в результате образуется матрица текста, число столбцов которой совпадает с числом букв лозунга. Столбцы матрицы затем переставляются в порядке следования букв лозунга при их размещении в стандартном алфавите латиницы. После этого текст из матрицы считывается построчно сверху вниз и разбивается на m-граммы. Композиция двух шифров в данном случае усложняет криптоанализ закрытых текстов и увеличивает ключевое пространство. Ключ состоит из исходного шифровального квадрата и слова-лозунга.

Рассмотрим пример. Пусть таблица билитеральной замены имеет вид:

	A	D	F	G	V	X
A	C	O		X	F
D	M	K		A	Z
F	N	W	L		J	D
G		S	I	Y	H	U
V	P		V	B		R
X	E	Q		T		G

Зашифруем следующую фразу «DON’T PUT IT OFF TILL TOMORROW». Тогда промежуточный шифртекст выглядит так:

«FXADFAXGVAGXXGGFXGADAVAVXGGFFFFFXGADDAADVXVXADFD».

Пусть слово-лозунг есть «GARDEN». Теперь применим к полученному тексту матричный шифр обхода:

4 1 6 2 3 5

G A R D E N

F X A D F A

X G V A G X

X G G F X G

A D A V A V

X G G F F F

F F X G A D

D A A D V X

V X A D F D

Теперь, считывая столбцы полученной матрицы в соответствии со старшинством букв лозунга и разбивая текст на блоки, получаем окончательно шифртекст:

«XGGDG FAXDA FVFGD DFGXA FAVFF XXAXF DVAXG VFDXD AVGAG XAA».

Здесь прервем описание исторических шифров, чтобы дать представление об одном методе криптоанализа, который был известен еще в средние века.

2. Частотный метод.

Шифры простой замены (так называют инъективные отображения множества заменяемых символов во множество замещающих) позволяют (при условии, что перехваченный шифртекст имеет достаточно большую длину) применить способ криптоанализа, который основан на учете частоты встречаемости символов алфавита естественных языков, для которых имеются соответствующие частотные таблицы. Существуют и более обширные таблицы частот биграмм и даже триграмм. В соответствии с такого рода данными криптоаналитик противника, подсчитывая частоты встречаемости символов в перехваченном шифртексте, может высказывать правдоподобные гипотезы о том, какие символы были заменены символами шифртекста. Такой подход весьма успешно работает, особенно для универсальных текстов большой длины. Рассматриваются поначалу те символы, которые встречаются наиболее часто. Если гипотеза не подтверждается, то переходят к следующим символам частотной таблицы имеющих наибольшую частоту из оставшихся. В русскоязычных текстах, например, наиболее часто встречающимся символом является символ пробела, а наиболее редкой буквой является «ф». Таким образом, шифр Полибия и шифр четырех квадратов могут быть вскрыты частотным методом.

Вернемся к историческим шифрам.

7) Шифр Б. де Виженера.

Полиалфавитный шифр – это шифр замены, при котором замещающий символ зависит от места в открытом тексте, на котором стоит заменяемый им символ. Шифрующая таблица Виженера представляет собой в случае латиницы квадрат 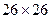, который заполнен буквами алфавита так, что каждая строка сдвинута на одну позицию вперед по отношению к предыдущей. При этом последние буквы приписываются спереди в соответствующем порядке. Таким образом, формально используются 26 алфавитов. Ключом служит некоторое слово на латинице, которое приписывается некоторое количество раз под открытым текстом, предварительно лишенным пробелов и знаков препинания и представляет собой единую строку. Строка закрытого текста получается по следующему правилу: для замены буквы открытого текста ее ищут в верхней строке таблицы Виженера, а стоящую под ней букву ключа – в левом столбце таблицы; замещающей буквой является та, что стоит на пересечении строки и столбца, в которых стоят заменяемая буква и соответствующая буква ключа. Текст, полученный таким образом, далее может быть разбит на m-граммы. Заметим, что это один из вариантов шифра Виженера. Ясно, что в этом случае одна и та же буква может заменяться разными в зависимости от попадания в пару с какой-либо ключевой буквой. Приведем пример. Имеется открытый текст:

“CHAUCER MET A YOUNG LADY AT COURT NAMED PHILIPPA”

Выберем ключевое слово:

“SHERIDAN”

Получим шифртекст:

CHAUCERMETAYOUNGLADYATCOURT NAMEDPH I LI PPA

SHE RI DANSHE RI DANS HER I DANSHE R I DANSHERI DAN

-------------------------------------------------------------------------------------

UOELKHRZWAEPWXNTDHHP IWCBMYXEI P EQHOMCQSPN

Если пробовать применять непосредственно к таким образом полученному шифртексту частотный метод, то легко видеть, что нарушенные частотные зависимости не оставляют шансов на успех. Но, как будет показано, положение спасает более тонкий подход. Используя тот факт, что длина ключа в примере равна восьми, запишем открытый текст в виде восьми подпоследовательностей:

С  E  L  U  P 

 H  T  A  R  H 

 A  A  D  T  I 

 U  Y  Y  N  L 

 C  O  A  A  I 

 E  U  T  M  P 

 R  N  C  E  P 

 M  G  O  D  A

Каждая из этих последовательностей преобразуется данным ключом по правилу сдвига по mod 26 на соответственно 18, 7, 4, 17, 8, 3, 0, 13 позиций.Поэтому, разбивая шифртекст на такие подпоследовательности, можнодля достаточно длинного текста при помощи обычного частотного анализа найти величины этих сдвигов. Остается проблема определения длины ключа. Для этого пытаются найти в шифртексте одинаковые биграммы и триграммы (т.е. буквосочетания из двух и трех букв). Предполагая, что они порождены одинаковыми биграммами и триграммами открытого текста, делают вывод, что величина расстояния между двумя одинаковыми k-граммами кратна длине ключа. Это позволяет сократить количество вариантов перебора.

Задача. Сообщение на русском языкезашифровано шифром Виженера в алфавите «А| Б| В| Г| Д| Е| Ж| З| И| Й| К| Л| М| Н| О| П| Р| С| Т| У| Ф| Х| Ц| Ч| Ш| Щ| Ъ| Ы| Ь| Э| Ю| Я| _ |, |. |? |!». Расшифровать сообщение

Дата добавления: 2014-11-16