
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решаем четыре системы сравнений 2 страница
|
|
|
|
ричная к третьей точке, в которой эта каса-
тельная пересекает кривую.
Покажем теперь, почему существует лишь
одна точка, в которой прямая l, проходящая
через точки Р и Q, пересекает кривую; един-
ственность определяет выражение для коор-
динат этой третьей точки, а затем и выраже-
ние для координат суммы Р + Q.
Пусть ( ), (
), ( ) и (
) и ( ) означают соответственно координаты точек P, Q и P + Q. Требуется выразить
) означают соответственно координаты точек P, Q и P + Q. Требуется выразить 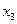 и
и  через координаты
через координаты  ,
, 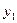 ,
,  и
и  . Допустим, что находимся в условиях случая (3) определения суммы P + Q и пусть
. Допустим, что находимся в условиях случая (3) определения суммы P + Q и пусть  х +
х + 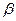 будет уравнением прямой, проходящей через точки P и Q (в случае (3) эта прямая не перпендикулярна оси х). Тогда
будет уравнением прямой, проходящей через точки P и Q (в случае (3) эта прямая не перпендикулярна оси х). Тогда  и
и  . Точка прямой l, т.е. точка (
. Точка прямой l, т.е. точка (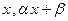 ) лежит на эллиптической кривой тогда и только тогда, когда
) лежит на эллиптической кривой тогда и только тогда, когда  ==
== 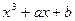 . Таким образом, для каждого корня уравнения третьей степени
. Таким образом, для каждого корня уравнения третьей степени

существует единственная точка пересечения. Известны, однако, два корня этого уравнения:  и
и  , где
, где  и
и  являются координатами точек P и Q, лежащих на этой кривой. Поскольку сумма корней приведенного уравнения третьей степени есть число противоположное коэффициенту при
являются координатами точек P и Q, лежащих на этой кривой. Поскольку сумма корней приведенного уравнения третьей степени есть число противоположное коэффициенту при  , то третьим корнем этого уравнения является
, то третьим корнем этого уравнения является 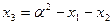 . Проводя вычисления для
. Проводя вычисления для 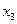 и P + Q =
и P + Q =  получаем выражения, зависящие от
получаем выражения, зависящие от  и
и  :
:
 ;
;
(11.2)
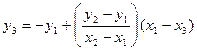 .
.
Случай (5), где P = Q, подобен этому с тем лишь, что коэффициент  теперь равен
теперь равен
производной  в точке Р. Дифференцирование функции, заданной вуравнении (11.1), приводит к выражению
в точке Р. Дифференцирование функции, заданной вуравнении (11.1), приводит к выражению  , из которого получаем
, из которого получаем
следующие выражения для координат точки 2Р:
 ;
;
(11.3)
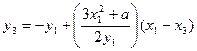 .
.
Пример. Пусть Р = (-3, 9) и Q = (-2, 8) будут точками кривой, заданной уравнением  . Найдем точки Р + Q и 2Р.
. Найдем точки Р + Q и 2Р.
Решение. Подставим  в первое из выражений (11.2). Получим
в первое из выражений (11.2). Получим  ; тогда второе из выражений дает
; тогда второе из выражений дает 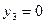 . Далее, подставим
. Далее, подставим  в первое из выражений (11.3) и получим 25/4 как координату х точки 2Р; координата y = -35/8 получается из второго выражения (11.3).
в первое из выражений (11.3) и получим 25/4 как координату х точки 2Р; координата y = -35/8 получается из второго выражения (11.3).
Теорема. Множество точек эллиптической кривой над полем К относительно операции сложения, определенной выше, образует абелеву группу.
Существует несколько способов доказательства того, что определение операции сложения точек эллиптической кривой наделяет указанное множество структурой абелевой группы. Но эту теорему доказывать не будем.
Так же, как и в случае произвольной абелевой группы, под n P будем понимать результат сложения точки Р с самой собой n раз, если n является положительным числом, в противном случае – это результат сложения точки –Р с самой собой | n | раз.
Скажем несколько слов о «точке в бесконечности» О. Из определения ясно, что она является нейтральным элементом группы. На нашем рисунке ее можно вообразить как точку, лежащую бесконечно далеко на оси y, предельного положения касательных к кривой. Она является «третьей точкой пересечения» каждой вертикальной прямой, пересекающей кривую; такая прямая пересекает кривую в точках вида (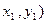 , (
, ( и О.
и О.
Определение. Порядок N точки Р, лежащей на эллиптической кривой, есть такое наименьшее натуральное число, что N P = O.
Очевидно, что такое число может не существовать. Часто важно знать точки конечного порядка на эллиптической кривой, определенной над полем Q.
Пример. Определим порядок точки Р = (2, 3) на кривой  .
.
Решение. Используя соотношения (5), получим 2Р = (0, 1); используя эти соотношения еще раз, получим 4Р = 2(2Р) = (0, -1). Так что 4Р = -2Р, откуда получаем, что 6Р = О. Таким образом, порядок Р может быть 2, 3 или 6. Но 2Р = (0, 1) 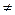 О, а если бы порядок был бы равен 3, то имели бы, что 4Р = Р, что, однако, неверно. Так что точка Р имеет порядок 6.
О, а если бы порядок был бы равен 3, то имели бы, что 4Р = Р, что, однако, неверно. Так что точка Р имеет порядок 6.
2. Эллиптические кривые над конечным полем.
До конца этого раздела К будет конечным полем F  , имеющем
, имеющем 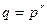 элементов. Пусть Е будет эллиптической кривой, определенной над полем F
элементов. Пусть Е будет эллиптической кривой, определенной над полем F  . Легко заметить, что
. Легко заметить, что
эллиптическая кривая Е может иметь самое большее 2 q + 1 F  -точек: точка в бесконечности и 2 q пар
-точек: точка в бесконечности и 2 q пар  , причем
, причем  F
F  , удовлетворяющих уравнению (11.1). Видно, что для каждого из q возможных значений х существует не более двух значений у, которые удовлетворяют уравнению (11.1).
, удовлетворяющих уравнению (11.1). Видно, что для каждого из q возможных значений х существует не более двух значений у, которые удовлетворяют уравнению (11.1).
Однако, поскольку только половина ненулевых элементов поля F  имеют квадратные корни, можно было ожидать, что (считая
имеют квадратные корни, можно было ожидать, что (считая 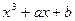 случайным элементом этого поля) количество F
случайным элементом этого поля) количество F  - точек на кривой в два раза меньше. Подробнее, пусть
- точек на кривой в два раза меньше. Подробнее, пусть  будет квадратичным характером поля F
будет квадратичным характером поля F  . Это отображение, которое каждому элементу х
. Это отображение, которое каждому элементу х  F
F  сопоставляет
сопоставляет  , в зависимости от того, имеет ли х квадратный корень в F
, в зависимости от того, имеет ли х квадратный корень в F  (и, кроме того,
(и, кроме того,  ). Например, если q = p – нечетное простое число, то
). Например, если q = p – нечетное простое число, то  есть символ Лежандра. Далее, число решений у
есть символ Лежандра. Далее, число решений у  F
F  уравнения
уравнения  всегда равно
всегда равно 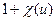 , а число решений уравнения (11.1) (вместе с точкой на бесконечности) есть
, а число решений уравнения (11.1) (вместе с точкой на бесконечности) есть
 . (11.4)
. (11.4)
Можно ожидать, что значение  будет одинаково часто равняться +1 и –1.
будет одинаково часто равняться +1 и –1.
Эта сумма напоминает суммирование в «случайном шаге»: бросается q раз монета, при выпадении орла делаем шаг вперед, при выпадении решки – шаг назад. Используя метод теории вероятностей, можно вычислить, что при q бросках монеты среднее значение, на которое отойдем, таким образом, от исходного положения, имеет порядок  . Сумма
. Сумма

подобна сумме в «случайном шаге», и оказывается, что для нее соответствующая оценка
есть 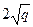 . Этот случай известен под названием теоремы Хассе.
. Этот случай известен под названием теоремы Хассе.
Теорема (Хассе).Пусть N будет количеством F  - точек на эллиптической кривой,
- точек на эллиптической кривой,
определенной над полем F  . Тогда
. Тогда
 .
.
3. Некоторые задачи.
Задача 1. Для эллиптической кривой  над полем F
над полем F  вычислить
вычислить
следующие композиции точек: 2(2, 2), 2(4, 6), (1, 3) + (1, 4), (2, 2) + (3, 2), (3, 5) + (5, 1).
Задача 2. Каждая из следующих точек имеет конечный порядок на данной
эллиптической кривой над Q. В каждом случае найти порядок Р.
(а) Р = (0, 16) на кривой  .
.
(b) P =  на кривой
на кривой  .
.
(с) Р = (3, 8) на кривой  .
.
Задача 3. Вычислить количество F 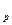 -точек для кривых.
-точек для кривых.
(а)  , p =7.
, p =7.
(b)  , p =13.
, p =13.
Задача 4. Найти эллиптическую кривую над полем F 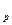 , имеющую максимальное
, имеющую максимальное
число F 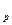 -точек для p =3 и p =5.
-точек для p =3 и p =5.
Раздел двенадцатый
Целью настоящего раздела является описание систем с открытым ключом, использующим конечную абелеву группу точек эллиптической кривой Е, определенной над полем F  . Легко проследить аналогию с группой F
. Легко проследить аналогию с группой F  - мультипликативной группой указанного конечного поля, где сложность задачи дискретного логарифмирования позволила построить систему с открытым ключом (например, систему ЭльГамала).
- мультипликативной группой указанного конечного поля, где сложность задачи дискретного логарифмирования позволила построить систему с открытым ключом (например, систему ЭльГамала).
1. Кратность точек. Операция аналогичная умножению двух элементов группы F  имеется и в группе точек эллиптической кривой Е, определенной над полем F
имеется и в группе точек эллиптической кривой Е, определенной над полем F  – сложение точек. Таким образом, операцией, аналогичной возведению в k -ю степень в F
– сложение точек. Таким образом, операцией, аналогичной возведению в k -ю степень в F  , является “умножение” точки Р
, является “умножение” точки Р  Е на целое число k. Возведение в k -ю степень в конечном поле может быть выполнено с помощью бинарного метода и требует
Е на целое число k. Возведение в k -ю степень в конечном поле может быть выполнено с помощью бинарного метода и требует  битовых операций. Подобным образом покажем, что кратное k P
битовых операций. Подобным образом покажем, что кратное k P  E может быть найдено с помощью
E может быть найдено с помощью

битовых операций при использовании бинарного метода (итерационного удваивания).
Пример. Чтобы найти 100Р, пишем 100Р = 2(2(Р+2(2(2(Р+2Р))))) и утверждаем, что
вычисления требуют 6 удваиваний и 2 сложений точек кривой.
Теорема. Пусть эллиптическая кривая Е определена с помощью уравнения Вейерштрасса (уравнение (11.1) из предыдущего раздела) над конечным полем F  . Тогда для произвольной точки Р
. Тогда для произвольной точки Р  Е координаты точки kP могут быть вычислены с помощью
Е координаты точки kP могут быть вычислены с помощью  битовых операций.
битовых операций.
Доказательство. Отметим, что требуется по меньшей мере 20 действий в F  (cло-
(cло-
жение, вычитание, умножение и деление), чтобы вычислить координаты суммы двух точек, используя выражения (11.2)-(11.3). Так как каждое такое сложение (или удвоение) может быть выполнено за время  , то при том, что бинарный метод требует
, то при том, что бинарный метод требует  шагов, получаем, что для вычисления координат точки k P достаточно
шагов, получаем, что для вычисления координат точки k P достаточно  битовых операций.
битовых операций.
Замечания.
1) Оценка времени в теореме не является наилучшей, особенно тогда, когда конечное поле имеет характеристику р = 2. Удовлетворимся же, однако, этой оценкой, возникающей в простейших алгоритмах, выполняющих действия в конечных полях.
2) Если известно число N точек нашей эллиптической кривой Е, и если k > N, то по-
скольку N P = O, можно при вычислении k P заменить число k его остатком от деления на N; в таком случае можем заменить прежнюю оценку времени работы на
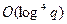 (напомним, что
(напомним, что  . Существует алгоритм, восходящий к Rene Schoof’у, вычисления N с помощью
. Существует алгоритм, восходящий к Rene Schoof’у, вычисления N с помощью  битовых операций.
битовых операций.
2. Кодирование открытых текстов. Требуется закодировать открытый текст с помощью точек некоторой эллиптической кривой, определенной над конечным полем F  . Требуется сделать это в соответствии с определенной регулярной процедурой так, чтобы открытый текст m (который можно считать натуральным числом из некоторого промежутка) мог быть легко восстановлен по координатам соответствующей ему точки Р
. Требуется сделать это в соответствии с определенной регулярной процедурой так, чтобы открытый текст m (который можно считать натуральным числом из некоторого промежутка) мог быть легко восстановлен по координатам соответствующей ему точки Р  . Отметим, что кодирование не то же самое, что шифрование. В дальнейшем опишем способы шифрования точек Р
. Отметим, что кодирование не то же самое, что шифрование. В дальнейшем опишем способы шифрования точек Р  , соответствующих открытым текстам. Причем важно, чтобы пользователи системы могли бы восстанавливать m при расшифровании соответствующих криптограмм.
, соответствующих открытым текстам. Причем важно, чтобы пользователи системы могли бы восстанавливать m при расшифровании соответствующих криптограмм.
Здесь нужно вспомнить о двух вещах. Во-первых, неизвестно на сегодняшний день ни одного полиномиального (от log q) детерминированного алгоритма, который способен выписать большое число точек произвольной эллиптической кривой Е над полем F  . Однако, как увидим в дальнейшем, существует вероятностный алгоритм с очень малой вероятностью неудачи. Во-вторых, недостаточно генерировать случайные точки на кривой Е: чтобы закодировать большое число возможных открытых текстов m, надо уметь генерировать систематическим образом точки как-то связанные с m, например, так, чтобы координата х такой точки была бы связана какой-то простой зависимостью с числом m.
. Однако, как увидим в дальнейшем, существует вероятностный алгоритм с очень малой вероятностью неудачи. Во-вторых, недостаточно генерировать случайные точки на кривой Е: чтобы закодировать большое число возможных открытых текстов m, надо уметь генерировать систематическим образом точки как-то связанные с m, например, так, чтобы координата х такой точки была бы связана какой-то простой зависимостью с числом m.
Рассмотрим теперь один из возможных вероятностных способов кодирования открытых текстов с помощью точек эллиптической кривой, определенной над полем F  , причем число
, причем число 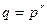 - большое (и нечетное). Пусть
- большое (и нечетное). Пусть  будет достаточно большим натуральным числом, чтобы вероятность неудачи порядка
будет достаточно большим натуральным числом, чтобы вероятность неудачи порядка  могла нас удовлетворить при кодировании единицы открытого текста m; на практике
могла нас удовлетворить при кодировании единицы открытого текста m; на практике  или в худшем случае
или в худшем случае  должно хватить. Предположим, что единицы текста m являются числами из промежутка
должно хватить. Предположим, что единицы текста m являются числами из промежутка 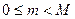 . Допустим также, что наше конечное поле выбрано так, что
. Допустим также, что наше конечное поле выбрано так, что 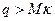 . Целое число в пределах от 1 до
. Целое число в пределах от 1 до  запишем в виде
запишем в виде  , где
, где 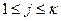 , и установим определенное взаимно однозначное соответствие между такими числами и элементами поля F
, и установим определенное взаимно однозначное соответствие между такими числами и элементами поля F  . Например, запишем каждое такое число как r -цифровое в позиционной системе с основанием р и считаем эти r цифр, трактуемые как элементы Z / p Z, коэффициентами многочлена степени r -1, отвечающего определенному элементу поля F
. Например, запишем каждое такое число как r -цифровое в позиционной системе с основанием р и считаем эти r цифр, трактуемые как элементы Z / p Z, коэффициентами многочлена степени r -1, отвечающего определенному элементу поля F  . Затем число (
. Затем число ( , отвечающее многочлену
, отвечающее многочлену 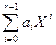 , который, будучи взятым по модулю некоторого неприводимого многочлена над F
, который, будучи взятым по модулю некоторого неприводимого многочлена над F  , назовем элементом поля F
, назовем элементом поля F  .
.
Таким образом, для данного числа m и произвольного числа  получим элемент х поля F
получим элемент х поля F  , отвечающий числу
, отвечающий числу  Для такого элемента х вычислим правую часть уравнения
Для такого элемента х вычислим правую часть уравнения
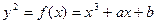
и пробуем найти корень квадратный из f(x), используя известный алгоритм для поиска квадратного корня по модулю р. Его можно без изменения перенести на произвольное поле F  . Правда, чтобы его применить, требуется определенный элемент g, который не является квадратом в этом поле; такие элементы легко находятся с помощью вероятностного алгоритма. Если найден такой элемент y, что
. Правда, чтобы его применить, требуется определенный элемент g, который не является квадратом в этом поле; такие элементы легко находятся с помощью вероятностного алгоритма. Если найден такой элемент y, что 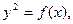 то берем Р
то берем Р  = (x, y). Если окажется, что элемент f(x) не является квадратом, то повторяем выбор х и проделываем все снова. Если же найдено х такое, что f(x) есть квадрат, то так как j не больше
= (x, y). Если окажется, что элемент f(x) не является квадратом, то повторяем выбор х и проделываем все снова. Если же найдено х такое, что f(x) есть квадрат, то так как j не больше  , то имеем возможность восстановить m по координатам точки (x, y) с помощью соотношения
, то имеем возможность восстановить m по координатам точки (x, y) с помощью соотношения  , где
, где  есть число, отвечающее элементу х в описанном выше взаимно однозначном соответствии между целыми числами и элементами поля F
есть число, отвечающее элементу х в описанном выше взаимно однозначном соответствии между целыми числами и элементами поля F  . Поскольку f(x) является квадратом для примерно 50% различных возможных х, вероятность того, что с помощью этого метода не будет построена точка Р
. Поскольку f(x) является квадратом для примерно 50% различных возможных х, вероятность того, что с помощью этого метода не будет построена точка Р  , координата которой х отвечает числу
, координата которой х отвечает числу  , лежащим между
, лежащим между  и
и  , есть около
, есть около  . (Точнее, вероятность того, что
. (Точнее, вероятность того, что 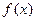 является квадратом есть N/ 2 q; однако, N /2 q очень близко к ½.)
является квадратом есть N/ 2 q; однако, N /2 q очень близко к ½.)
3. Дискретный логарифм на кривой Е. Ранее обсуждались криптосистемы с открытым
ключом на основе сложности задачи дискретного логарифмирования в мультипликативной группе конечного поля. Теперь то же сделаем для аддитивной группы точек эллиптической кривой Е над конечным полем F  .
.
Определение. Порядок группы точек эллиптической кривой над конечным полем F  называется порядком этой кривой.
называется порядком этой кривой.
Определение. Если Е есть эллиптическая кривая над полем F  и В есть точка этой кривой, то задача дискретного логарифмирования на кривой Е (по основанию В) состоит в нахождении для данной точки Р
и В есть точка этой кривой, то задача дискретного логарифмирования на кривой Е (по основанию В) состоит в нахождении для данной точки Р  Е целого числа х
Е целого числа х  Z такого, что х В = Р, если такое число х существует.
Z такого, что х В = Р, если такое число х существует.
Возможно, задача дискретного логарифмирования на эллиптической кривой окажется более трудной, чем аналогичная задача для дискретного логарифма в конечном поле. Об этом говорит то, что лучшие алгоритмы, разработанные для конечных полей, не работают в случае эллиптических кривых.
До 1990 года единственными алгоритмами, находящими дискретный логарифм на эллиптической кривой, были алгоритмы, действующие в произвольной группе, не использующие специальной структуры этой группы. Это были алгоритмы, работающие за экспоненциальное время при условии, что порядок группы делится на большое простое число.
Опишем теперь криптографические системы аналогичные системам с открытым ключом, основанные на задаче дискретного логарифмирования, но теперь для группы точек эллиптической кривой Е, определенной над конечным полем F  .
.
4. Система аналогичная системе выработки ключа Диффи-Хеллмана (см. р.16). Допустим, что Алиса и Боб хотят согласовать ключ, который будут использовать затем в некоторой криптографической системе. Во-первых, выбирают (не делая из этого тайны) конечное поле F  и эллиптическую кривую Е над этим полем. Их ключ будет сконструирован из определенной случайной точки Р на этой кривой. Если, например, выбрать случайную точку Р
и эллиптическую кривую Е над этим полем. Их ключ будет сконструирован из определенной случайной точки Р на этой кривой. Если, например, выбрать случайную точку Р  Е, то ее координата х будет случайным элементом поля F
Е, то ее координата х будет случайным элементом поля F  и может быть представлена в виде r -цифрового целого числа, записанного в позиционной системе с основанием р (где
и может быть представлена в виде r -цифрового целого числа, записанного в позиционной системе с основанием р (где 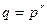 ), которое было бы ключом в их классической криптографической системе. (Слово «случайная» имеет то значение, что выбор ключа является вычислительно произвольным, и нет способа предвидеть, который из возможных ключей окончательно выбран). Их задачей является выбор точки Р таким образом, чтобы сами сообщения между ними могли быть открытыми, и никто, кроме них, не смог бы догадаться, какой точкой является Р.
), которое было бы ключом в их классической криптографической системе. (Слово «случайная» имеет то значение, что выбор ключа является вычислительно произвольным, и нет способа предвидеть, который из возможных ключей окончательно выбран). Их задачей является выбор точки Р таким образом, чтобы сами сообщения между ними могли быть открытыми, и никто, кроме них, не смог бы догадаться, какой точкой является Р.
Алиса и Боб, во-первых, явным образом выбирают точку В  Е – будущее «основание». Точка В выполняет роль порождающего элемента g в мультипликативной группе конечного поля в системе Диффи-Хеллмана. Не будем рассматривать случай, когда точка В является порождающим элементом группы точек кривой Е. В действительности эта группа может не быть циклической. Даже если она циклична, то уклоняемся от доказательства того, что В есть образующий элемент (или даже вычисления числа N точек, которое вообще можем не знать). Требуется, однако, чтобы подгруппа, образованная В была большой, лучше всего, если ее мощность будет того же порядка, что и мощность самой группы Е. Теперь же допустим, что В выбрано и является известной точкой кривой Е, порядок которой очень большой (или точно равен N, или является большим делителем числа N).
Е – будущее «основание». Точка В выполняет роль порождающего элемента g в мультипликативной группе конечного поля в системе Диффи-Хеллмана. Не будем рассматривать случай, когда точка В является порождающим элементом группы точек кривой Е. В действительности эта группа может не быть циклической. Даже если она циклична, то уклоняемся от доказательства того, что В есть образующий элемент (или даже вычисления числа N точек, которое вообще можем не знать). Требуется, однако, чтобы подгруппа, образованная В была большой, лучше всего, если ее мощность будет того же порядка, что и мощность самой группы Е. Теперь же допустим, что В выбрано и является известной точкой кривой Е, порядок которой очень большой (или точно равен N, или является большим делителем числа N).
|
|
|
|
|
Дата добавления: 2014-11-16; Просмотров: 465; Нарушение авторских прав?; Мы поможем в написании вашей работы!