Решаем четыре системы сравнений 4 страница

Определение. Пусть G – генератор с расширением l. Обозначим через случайную величину G (x) со значениями в для х, которое равномерно распределено на 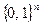. Через 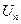обозначим случайную величину, равномерно распределенную на 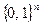. Генератор G называется псевдослучайным, если ансамбл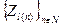и и 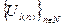неразличимы за полиномиальное время. Двоичную последовательность G (x), полученную с помощью псевдослучайного генератора G, называют псевдослучайной.

Интересно то, что расширение l не играет принципиальной роли как количественная характеристика генератора. Оказывается, как это видно из следующей теоремы, генератор с минимальным расширением можно превратить в генератор с произвольным расширением.

Теорема (Гольдрайх, Микели). Из произвольного псевдослучайного генератора G с расширением можно получить псевдослучайный генератор 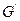с расширением 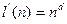для произвольной целой константы d >1.

Псевдослучайные генераторы целиком подходят для использования в вероятностных алгоритмах. Имеется связь псевдослучайных генераторов с односторонними функциями. Именно, существует

Теорема. Псевдослучайные генераторы существуют, если и только если существуют односторонние функции.

2. Криптографические приложения.

В криптографии от псевдослучайных генераторов G требуется выполнение следующего условия. Пусть противник наблюдает случайную величину G(x), распределенную на и порожденную равномерным распределением х на 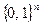. Допустим, что сначала ему открываются лишь первые i битов величины G(x). Тогда требуется, чтобы противник не мог предсказать i+ 1-й бит с вероятностью, существенно большей ½. Иными словами, криптограф заинтересован в том, чтобы не было лучшего пути получить i+ 1-й бит на основе знания предыдущих битов нежели простым угадыванием. Связь такого требования с криптографической стойкостью можно пояснить таким примером. Пусть противник перехватил шифртекст в двоичном алфавите, и ему известны следующие факты:

1) использован шифр одноразового блокнота;

2) ключом является псевдослучайная последовательность;

3) открытый текст начинается словами “Dear Sir!”.

Прибавив известный ему префикс открытого текста к соответствующему префиксу шифртекста, противник получает первые i битов псевдослучайного ключа. Если генератор, который был использован для выбора ключа, не обладает описанным выше свойством, то противник может экстраполировать следующие биты ключа и добыть из шифртекста еще больше информации.

Определение. Пусть для каждого натурального n случайная величина принимает значения в 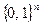. Ансамбль 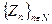называется непредсказуемым, или, как еще говорят, выдерживает тестирование следующего бита, если выполняется такое условие. Допустим, что 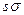– префикс случайного слова , где и , причем длина k этого префикса является случайным числом от 1 до n. Пусть А – произвольный полиномиальный вероятностный алгоритм, который получает на вход s. Тогда

для произвольного полинома р и достаточно больших n.

Оказывается, что псевдослучайные генераторы и только они обладают свойством непредсказуемости.

Теорема. Пусть 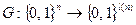– генератор с расширением l. Обозначим через случайную величину G(x) со значениями в для х, равномерно распределенного на 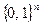. Генератор G является псевдослучайным тогда и только тогда, когда ансамбль 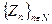непредсказуем.

На основании вышесказанного, псевдослучайные генераторы называют криптографически надежными.

3. Возвращение к односторонним функциям.

Как известно, функции RSA, SQUARE, EXP предполагаются односторонними. После фиксации соответствующих параметров эти функции становятся перестановками некоторого множества D. Имея ввиду эти примеры, рассмотрим эффективно вычислимое биективное отображение 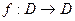. Одновременно рассмотрим эффективно вычислимый предикат – для каждого легко можно вычислить бит 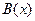. Пусть 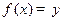. Поскольку f – биекция, то 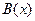однозначно определяется элементом y. Однако, это не означает, что имея y, легко получить 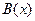. Если нет эффективного алгоритма, который бы для большинства элементов по заданному значению 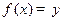давал бы бит 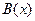, то предикат В называется ядром функции f. Совершенно ясно, что если функция (биекция) имеет ядро, то она односторонняя. Действительно, если бы был эффективный алгоритм для вычисления 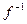, то 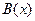можно было бы легко получить из у композицией алгоритмов для вычисления 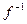и В.

Дадим формальное определение этому понятию. Пусть 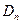– последовательность множеств, для которой .

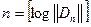Определение. Полиномиально вычислимый предикат В, называется ядром функции , если любой полиномиальный вероятностный алгоритм на входе f(x), где х – случайный элемент из 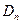, дает значение 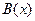с вероятностью меньшей, чем 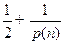для произвольного полинома р и достаточно большого n. Вероятность берется по случайному выбору х и по случайной последовательности вероятностного алгоритма.

По сути, определение говорит, что нет никакого лучшего способа получить 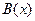по f(x), чем просто взять наугад случайный бит.

Для указанных выше функций предложены следующие предикаты: для функции с фиксированными параметрами e и m, а также для функции 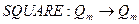с фиксированным параметром m, B есть предикат четности, т.е. 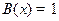для нечетных n и только для них. Для функции 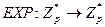с фиксированными параметрами p и g предикат B задается соотношением

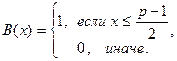
Раздел пятнадцатый

1. Одна схема псевдослучайного генератора.

Пусть f – односторонняя функция, которая после фиксации соответствующих параметров является перестановкой некоторого множества , причем 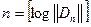. Примерами являются функции RSA, SQUARE, EXP, которые означают перестановки множеств Z , и Z 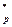соответственно. Пусть В – ядро функции f. Используя f и B, сконструируем генератор G с расширением l(n), где функция l(n) ограничена некоторым полиномом от n. Считаем, что 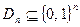и что принадлежность этому множеству можно эффективно распознать.

Вход: .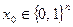

1) Если 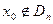, то остановиться. Иначе, продолжать.

2) Для вычислить и .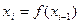

3) Дать на выход последовательность .

Теорема. Для каждой односторонней перестановки f и ее ядра B описанный генератор G является псевдослучайным.

Замечание. Теорема говорит о том, что если 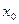выбирается равновероятно из 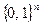, то никакой полиномиальный вероятностный алгоритм не в состоянии отличить последовательность 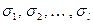от настоящей случайной последовательности такой же длины. На самом деле это утверждение остается справедливым и когда обнародуется последний элемент , т.е. последовательность нельзя отличить от последовательности за полиномиальное время, где 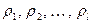– случайные и независимые между собой биты. Отметим, что и является случайным элементом множества .

Остановимся на реализации конструкции, описанной выше, на основе функции Рабина. Генератор, который при этом получается, называется генератором BBS (L.Blum, M. Blum, М. Shuba).

Пусть параметр ограничен полиномом от n. Чтобы получить из n случайных битов l псевдослучайных нужно:

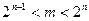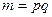1) выбрать случайные простые р и q такие, что для и ;

2) выбрать случайный элемент 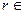Z 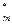и вычислить ;

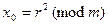3) для i от 1 до l вычислять

, ;

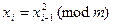4) дать на выход последовательность .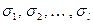

Легко видеть, что здесь выдержана общая конструкция, описанная выше, с функцией 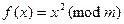и ее ядром, предикатом четности 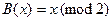. Следует напомнить, что функция 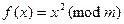не является биекцией на Z , но является таковойна . Именно поэтому выбиралось 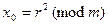– случайный элемент множества . По предыдущей теореме BBS генератор является псевдослучайным, а значит,

криптографически надежным (при условии, что функция SQUARE действительно является односторонней). Некоторые его свойства являются особенно удобными.

Теорема. По и простым р и q можно эффективно вычислить всю последовательность 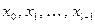, а значит, и последовательность .

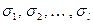Доказательство. Допустим, что известен элемент 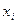, где 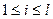. Покажем, как получить 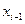. Ввиду биективности функции 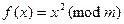на , элемент 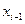однозначно определяется такими условиями:

, .

Введем обозначение 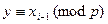и 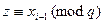. По Китайской теореме вычеты у и z удовлетворяют условиям:

(15.1) и

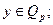
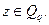(15.2) и, более того, такая пара однозначно определяет 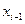, причем эффективным образом. Так что достаточно найти у и z. Для этого используем соотношения:

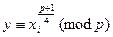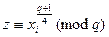, . (15.3)

Из них непосредственно видно, что у и z вычисляются эффективно с применением бинарного метода. Остается проверить условия (15.2) и (15.1). Условие (15.2) вытекает из замкнутости умножения в 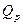и 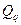. Условие (15.3) вытекает из формулы извлечения корня квадратного по модулю простого, сравнимого с 3 по (mod 4).

2. Приложение к поточным шифрам.

Поточным, как известно, называется шифр, который двоичное сообщение , используя двоичный ключ такой же длины 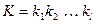, превращает в шифртекст 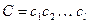путем покомпонентного сложения М и К по mod 2, т.е. 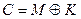. Разновидности поточных шифров различаются между собой способом выработки ключа (ключевой гаммы). В шифре одноразового блокнота каждый бит гаммы выбирается случайно и независимо от остальных битов. Это влечет абсолютную надежность шифра в теоретико-информационном смысле. Однако это же обстоятельство делает шифр одноразового блокнота непрактичным для передачи длинных сообщений. Выходом может служить генерация ключа К с помощью криптографически надежного генератора псевдослучайных битов. При этом ключом можно называть не всю последовательность, а лишь начальный элемент, который используется при ее генерации.

3. Криптосистема Блюма-Гольдвассера.

1) Генерирование ключей.

Выбирают два больших простых числа Блюма р и q. Полагают открытым ключом произведение 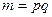, а секретным ключом – р и q.

2) Шифрование.

Чтобы зашифровать двоичную последовательность длины l Алиса формирует двоичную последовательность 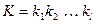из l псевдослучайных битов, полученных с помощью BBS генератора. Для этого она предварительно выбирает случайный квадратичный вычет 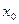по mod m, последовательным возведением в квадрат получает последовательность и полагает 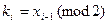. Далее Алиса

вычисляет 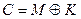и посылает Бобу шифртекст, который состоит из пары 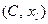. Заметим, что описанное шифрование является вероятностным, ибо при разных выборах 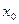для генерирования псевдослучайной последовательности К сообщению будут соответствовать разные шифртексты.

3) Расшифрование.

Боб, который знает секретный ключ р и q, по числу вычисляет все члены последовательности 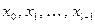(вычисления проводятся в обратном порядке, как это описано в последней теореме). На основе этой последовательности Боб воссоздает двоичный вектор К и получает

.

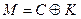Эффективность. По скорости работы эта система сравнима с RSA.

Стойкость. Доказано, что система является стойкой при условии сложности задачи факторизации целых чисел Блюма. Один из вариантов соответствующей теоремы звучит так: для любого сообщения М длины 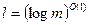случайную величину 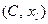невозможно отличить от величины 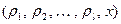, которая состоит из настоящей случайной двоичной последовательности 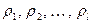и случайного квадратичного вычета 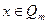никакой схемой полиномиального от l размера.

Пример. Пусть 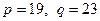– секретный ключ. Тогда открытым ключом будет . Пусть нужно зашифровать сообщение “NO”. Запишем сообщение в двоичной форме:

М = 001101 001110.

Запустим BBS генератор, выбрав r = 233. Потребуются 12 псевдослучайных битов. Их можно получить в соответствии с вышеописанной схемой.

i

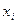
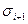
Получаем К = 101011 100111 и . Тогда величина С имеет вид:

С = 100110 101001.

Таким образом, шифртекстом будет пара (100110 101001, 6).

Раздел шестнадцатый

Под криптографическим протоколом будем понимать набор правил или соглашений, которые устанавливают для себя стороны, участники протокола, для совместного достижения определенной цели. Указанный набор можно представлять, как некий распределенный алгоритм, снаб

женный спецификациями форматов сообщений между участниками, синхронизации их действий и правилами поведения при возможных сбоях.

Криптопротоколы решают задачи обеспечения целостности и достоверности передаваемой информации, а также ее неотслеживаемости. Есть и некоторые другие отличия от собственно криптосистем. Это, во-первых, то, что протоколы, как правило, носят интерактивный характер, когда в процессе выполнения их участники неоднократно обмениваются сообщениями, во-вторых, участников протокола может быть более двух, в-третьих, участники могут не доверять друг другу.

Для того, чтобы протокол приводил к желаемой цели, необходимо выполнение следующих условий:

1) корректность протокола – совокупность действий, предусмотренных протоколом, должна обеспечить получение требуемого результата при всех возможных условиях;

2) полнота и однозначность определения – должны быть специфицированы действия каждого участника протокола для всех возможных ситуаций;

3) непротиворечивость протокола – результаты, полученные различными участниками, не должны противоречить друг другу;

4) осведомленность и согласие участников – каждый субъект должен заранее знать протокол и все шаги, которые должен выполнить; все субъекты должны быть согласны играть свою роль.

Это молодая ветвь криптологии начала бурно развиваться с появлением идеологии открытого ключа. Особенно сильный толчок развитию криптографических протоколов дает широкий переход на электронную форму взаимоотношений сторон в сфере бизнеса. Здесь рассматриваются несколько типов протоколов, которые реализуются на основе описанных выше понятий и конкретных криптосистем. Во всех случаях для простоты предполагаем, что участниками протокола являются две стороны, традиционно именуемые Алисой и Бобом.

1. Протокол обмена ключами.

Проблема пересылки ключей возникает при использовании симметричных криптосистем, которые не вышли из употребления, например, по причине применения, в целом, более быстрых алгоритмов зашифрования и расшифрования, что бывает важным при обмене сообщениями большого объема.

Будем считать, что Алиса и Боб договорились о конфиденциальной переписке и желают выработать общий секретный ключ. Обозначения здесь совпадают с соответствующими обозначениями, использованными в описании системы ЭльГамала. Итак,

1) Алиса выбирает большое простое число р и первообразный корень g по mod p

и посылает их открыто Бобу.

2 ) Алиса выбирает случайное число а в пределах от 1 до р – 1, а Боб – случайное

число b в тех же границах.

3) Алиса вычисляет g (mod p) и посылает его Бобу, а Боб вычисляет g 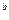(mod p) и

посылает его Алисе.

4) Алиса и Боб вычисляют одно и то же число 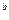(g 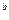) = (g ) = g (mod p), которое

и принимается за общее значение ключа.

Противник, перехватив значения p, g, g , g 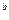и стремясь получить число g , вынужден решать задачу дискретного логарифмирования аналогичную той, что возникает при попытке слома криптосистемы ЭльГамала.

Рассмотрим пример. Пусть выбрано простое число р = 9995647. Первообразным корнем по mod 9995647 является число g = 3. Предположим, что Алиса выбрала случайным образом число а = 35771, а Боб выбрал случайное число b = 27453. Тогда Алиса посылает Бобу число 3 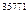= 1076844 (mod 9995647), А Боб, в свою очередь, посылает Алисе число 3 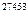= 5062474 (mod 9995647). В итоге оба участника протокола вычисляют общее значение секретного ключа

g = (3 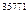) 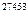= 8587885 (mod 9995647).

Дата добавления: 2014-11-16