Решаем четыре системы сравнений 9 страница

Следствие. Для каждого конечного поля 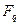и каждого натурального числа 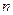в кольце 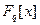существует неприводимый многочлен степени .

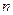Последние результаты подсказывают способ построения конечного поля данного порядка как расширения его простого подполя. Действительно, если 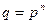, то следует задать неприводимый многочлен степени 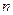над полем 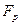. Любой корень 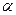такого многочлена имеет степень 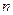над полем 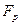. Поэтому, присоединяя такой корень к ,

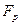получаем простое алгебраическое расширение 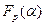такое, что , а базисом расширения будет система 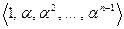. Значит, любой элемент 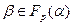может быть представлен в виде линейной комбинации

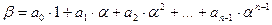, где .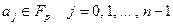

В силу единственности конечного поля из 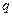элементов можно отождествить .

Пример 2. Пусть требуется построить поле 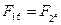. Рассмотрим неприводимый многочлен 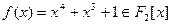. Его неприводимость можно легко проверить простыми средствами. Пусть 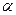– корень 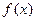, т.е. в поле разложения этого многочлена над полем 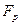. Тогда в соответствии с указанным выше рассуждением любой элемент 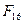может быть представлен в ви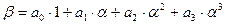де:

, где .

Следовательно,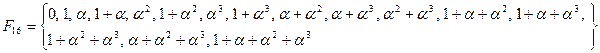

Сложение элементов такого поля есть обычное приведение подобных слагаемых по 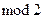. При выполнении операции умножения требуется привести элементы к виду, указанному выше. Поэтому следует воспользоваться равенством , что влечет за собой взятие остатка при формальном делении на многочлен . Составим теперь таблицу индексов для элементов мультипликативной группы поля, т.е. 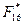. Для этого требуется найти примитивный элемент поля. Простой проверкой убеждаемся, что таковым элементом является корень 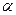. Таким образом, . Тогда таблица индексов будет выглядеть так.

j		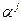j		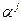j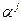

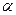
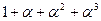
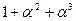
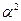
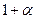
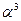
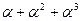
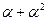
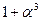
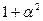
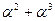
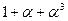
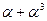
Таблица индексов позволяет быстро получать произведения элементов конечного поля.

Элементы поля 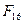можно представлять классами факторкольца , что, очевидно, приведет к изображению элементов поля подобно тому, как показано выше.

Рассмотрим еще на этом же примере способ матричного представления элементов конечного поля. Идея такого представления состоит в том, что матрица вида

А =

есть характеристическая матрица многочлена

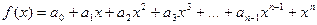, т.е.

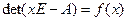. По теореме Гамильтона Кэли 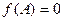. Таким образом, эта матрица может рассматриваться как корень многочлена 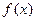. Именно, как аналог корня 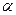. Тогда в качестве базиса можно выбрать систему матриц 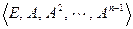. В частном случае нашего примера имеем:

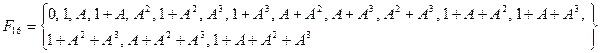
или

Операциями над элементами поля теперь служат обычные матричные операции сложения и умножения по .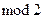

Дата добавления: 2014-11-16