
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решаем четыре системы сравнений 6 страница
|
|
|
|
Теперь можно вычислить доли секрета s 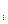 , 1
, 1  i
i  9 и проверочные величины r
9 и проверочные величины r 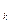 , 0
, 0  k
k  5.
5.
s  = f (1) = 2369220, r
= f (1) = 2369220, r  = 5580745,
= 5580745,
s  = f (2) = 7656145, r
= f (2) = 7656145, r  = 9839841,
= 9839841,
s  = f (3) = 3767974, r
= f (3) = 3767974, r  = 17831867,
= 17831867,
s 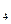 = f (4) = 19300855, r
= f (4) = 19300855, r  = 13632202,
= 13632202,
s  = f (5) = 1867347, r
= f (5) = 1867347, r 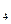 = 19609246,
= 19609246,
s 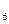 = f (6) = 457656, r
= f (6) = 457656, r  = 10437177.
= 10437177.
s  = f (7) = 18087474,
= f (7) = 18087474,
s 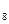 = f (8) = 16621232,
= f (8) = 16621232,
s  = f (9) = 23045629;
= f (9) = 23045629;
Легко проверить следующее равенство, вычисляя независимо его левую и правую части:
g  = r
= r  r
r  r
r  r
r  r
r 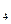 r
r  = 15344665 (mod 25362569).
= 15344665 (mod 25362569).
Восстановление секрета s по любым шести значениям s 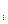 , 1
, 1  i
i  9, производится по указанной выше интерполяционной формуле Лагранжа.
9, производится по указанной выше интерполяционной формуле Лагранжа.
8. Некоторые задачи.
Задача 1. Выработать подпись на основе RSA под данным сообщением и проверить ее, если открытые ключи корреспондентов равны:  ,
,  ,
, 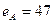 ,
,  .
.
Сообщение: «Шторм».
Алфавит: «|а|б|в|г|д|е|ж|з|и|й|к|л|м|н|о|п|р|с|т|у|ф|х|ц|ч|ш|щ|ъ|ы|ь|э|ю|я|».
Задача 2. Выработать подпись на основе RSA под данным сообщением и проверить ее, если открытые ключи корреспондентов равны:  ,
,  ,
, 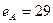 ,
,  .
.
Сообщение: «Гомер».
Алфавит: «|а|б|в|г|д|е|ж|з|и|й|к|л|м|н|о|п|р|с|т|у|ф|х|ц|ч|ш|щ|ъ|ы|ь|э|ю|я|».
Задача 3. Выработать подпись на основе RSA под данным сообщением и проверить ее, если открытые ключи корреспондентов равны:  ,
,  ,
,  ,
, 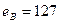 .
.
Сообщение: «Яшма».
Алфавит: «|а|б|в|г|д|е|ж|з|и|й|к|л|м|н|о|п|р|с|т|у|ф|х|ц|ч|ш|щ|ъ|ы|ь|э|ю|я|».
Задача 4. Выработать подпись на основе протокола ЭльГамала под данным сообщением и проверить ее, если известен открытый ключ:  ,
, 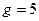 ,
,  .
.
Сообщение: «Бор».
Алфавит: «|а|б|в|г|д|е|ж|з|и|й|к|л|м|н|о|п|р|с|т|у|ф|х|ц|ч|ш|щ|ъ|ы|ь|э|ю|я|».
Задача 5. Выработать подпись на основе протокола ЭльГамала под данным сообщением и проверить ее, если известен открытый ключ: 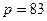 ,
, 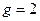 ,
, 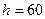 .
.
Сообщение: «Тор».
Алфавит: «|а|б|в|г|д|е|ж|з|и|й|к|л|м|н|о|п|р|с|т|у|ф|х|ц|ч|ш|щ|ъ|ы|ь|э|ю|я|»
Задача 6. Выработать подпись на основе протокола ЭльГамала под данным сообщением и проверить ее, если известен открытый ключ:  ,
, 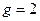 ,
,  .
.
Сообщение: «Тест».
Алфавит: «|а|б|в|г|д|е|ж|з|и|й|к|л|м|н|о|п|р|с|т|у|ф|х|ц|ч|ш|щ|ъ|ы|ь|э|ю|я|».
ПРИЛОЖЕНИЕ
Раздел семнадцатый
1. Парадокс дней рождений.
Рассмотрим следующую задачу для произвольной функции  , где
, где  – множество, состоящее их
– множество, состоящее их 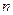 элементов.
элементов.
Найти величину k для оценки вероятности  (т.е.
(т.е. 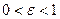 ), такую, что для k попарно различных элементов
), такую, что для k попарно различных элементов 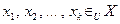 (т.е. выбранных равновероятно из множества X) набор, состоящий из k значений функции
(т.е. выбранных равновероятно из множества X) набор, состоящий из k значений функции 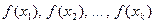 , удовлетворяет неравенство
, удовлетворяет неравенство
 для некоторых
для некоторых  .
.
Иначе говоря, при k вычислениях функции коллизия возникает с вероятностью не меньше  .
.
В этой задаче требуется найти число k, которое удовлетворяет некоторой оценке вероятности снизу для любой функции. Предполагается лишь, что функция обладает так называемым свойством случайности: такие функции отображают равномерно распределенные числа из множества X в равномерно распределенные числа из множества Y. Очевидно, что только такая функция позволяет увеличить число k при заданной оценке вероятности так, чтобы эти условия выполнялись для любой функции при той же оценке вероятности. Следовательно, необходимо, чтобы 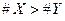 . В противном случае могут существовать функции, у которых коллизии вообще не возникают.
. В противном случае могут существовать функции, у которых коллизии вообще не возникают.
Итак, можно предположить, что вычисление функции в этой задаче порождает n разных и равновероятных точек. Эти вычисления можно отождествить с извлечением шаров из урны, содержащей n разноцветных шаров, после чего цвет записывается, и шар возвращается в урну. Следовательно, задача заключается в поиске такого числа k, при котором какой-нибудь цвет повторялся бы с вероятностью  .
.
На цвет первого шара не налагаются никакие ограничения. Пусть 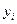 – цвет шара, извлеченного при i -ой попытке. Цвет второго шара не должен совпадать с цветом первого шара, поэтому вероятность того, что
– цвет шара, извлеченного при i -ой попытке. Цвет второго шара не должен совпадать с цветом первого шара, поэтому вероятность того, что  , равна
, равна 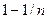 , вероятность того, что
, вероятность того, что  и
и 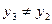 , равна
, равна  и т.д. При извлечении k -го шара вероятность того, что до этого не возникает коллизия, равна
и т.д. При извлечении k -го шара вероятность того, что до этого не возникает коллизия, равна
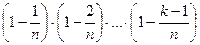 .
.
При достаточно большом числе n и относительно малом числе x выполняется следующее соотношение:
 ,
,
или
 .
.
Итак,
 .
.
Полученное число представляет собой вероятность извлечь k шаров без коллизии. Следовательно, вероятность возникновения по крайней мере одной коллизии равна
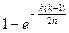 .
.
Приравнивая эту величину к числу  , получаем
, получаем
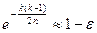 ,
,
или
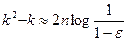 .
.
Иначе говоря,
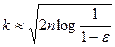 . (17.1)
. (17.1)
Итак, для случайной функции, отображающей множество X на множество Y, необходимо выполнить по крайней мере 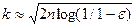 вычислений, чтобы обнаружить коллизию с заданной вероятностью
вычислений, чтобы обнаружить коллизию с заданной вероятностью  . Из соотношения (17.1) вытекает, что даже если число
. Из соотношения (17.1) вытекает, что даже если число  достаточно велико (т.е. очень близко к 1), величина
достаточно велико (т.е. очень близко к 1), величина 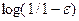 остается весьма малой, а значит, в принципе, число k прямо пропорционально
остается весьма малой, а значит, в принципе, число k прямо пропорционально 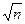 .
.
Если 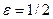 , то
, то
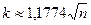 . (17.2)
. (17.2)
Зависимость числа k от величины n, выявленная формулами (17.1) и (17.2), означает, что для случайной функции, пространство исходов которой состоит из n точек, чтобы обнаружить коллизию со значимой вероятностью, необходимо выполнить всего 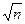 вычислений.
вычислений.
Этот факт оказал значительное влияние на разработку криптосистем и криптографических протоколов. Например, если корень квадратный, извлеченный из размера фрагмента данных (скажем, криптографического ключа или сообщения), скрытого в качестве прообраза криптографической функции (которая, как правило, является случайной), не является достаточно большой величиной, данные можно расшифровать с помощью случайных вычислений значения функции. Такая атака получила название «атака по методу квадратного корня», или «атака на основе парадокса дней рождения». Второе название возникло из-за внешне парадоксального явления: положив  в формуле (17.2), получим
в формуле (17.2), получим  . Иначе говоря, для того, чтобы с вероятностью более 50% обнаружить двух людей, родившихся в один и тот же день и находящихся в комнате, заполненной случайными людьми, достаточно, чтобы в комнате было всего 23 человека. Эта величина кажется слишком маленькой по сравнению с интуитивно ожидаемой.
. Иначе говоря, для того, чтобы с вероятностью более 50% обнаружить двух людей, родившихся в один и тот же день и находящихся в комнате, заполненной случайными людьми, достаточно, чтобы в комнате было всего 23 человека. Эта величина кажется слишком маленькой по сравнению с интуитивно ожидаемой.
2. Применение парадокса дней рождения: алгоритм кенгуру Полларда.
Пусть р – простое число. При определенных условиях функция возведения в степень по модулю  является, по существу, случайной. Иначе говоря, для чисел
является, по существу, случайной. Иначе говоря, для чисел 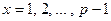 значения
значения 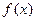 случайным образом разбросаны по промежутку
случайным образом разбросаны по промежутку 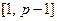 . Это уже обсуждавшаяся функция
. Это уже обсуждавшаяся функция  из р.13, являющаяся кандидатом в односторонние функции.
из р.13, являющаяся кандидатом в односторонние функции.
Иногда для значения 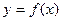 известно, что
известно, что  при некоторых значениях a и b. Очевидно, что, вычисляя значения
при некоторых значениях a и b. Очевидно, что, вычисляя значения  и т.д., можно найти число х за
и т.д., можно найти число х за  шагов. Если число
шагов. Если число  слишком велико, то такой метод перебора будет непрактичным. Однако, если число
слишком велико, то такой метод перебора будет непрактичным. Однако, если число  не слишком велико (например,
не слишком велико (например, 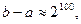 то
то  , что является вполне разумной величиной), то при обращении функции
, что является вполне разумной величиной), то при обращении функции 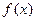 за
за  шагов проявляется парадокс дней рождения. Используя этот факт, Поллард изобрел метод дискретного логарифмирования, получивший в итоге название
шагов проявляется парадокс дней рождения. Используя этот факт, Поллард изобрел метод дискретного логарифмирования, получивший в итоге название  -метод, или метод кенгуру.
-метод, или метод кенгуру.
Поллард описал свой алгоритм, используя в качестве персонажей двух кенгуру – домашнего, Т, и дикого, W. Задача вычисления индекса 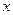 с помощью функции
с помощью функции 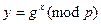 сводилась к ловле кенгуру
сводилась к ловле кенгуру  с помощью кенгуру
с помощью кенгуру 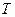 . Эту задачу можно решить, позволив обоим кенгуру прыгать вокруг по определенным траекториям. Пусть
. Эту задачу можно решить, позволив обоим кенгуру прыгать вокруг по определенным траекториям. Пусть  – множество целых чисел, состоящее из
– множество целых чисел, состоящее из  элементов (
элементов (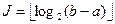 , а значит, является достаточно малым числом):
, а значит, является достаточно малым числом):
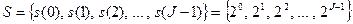 .
.
Каждый раз один из кенгуру прыгает на расстояние, которое случайным образом извлекается из множества  , причем общее расстояние, пройденное каждым из кенгуру, регистрируется с помощью счетчика.
, причем общее расстояние, пройденное каждым из кенгуру, регистрируется с помощью счетчика.
Кенгуру Т начинает свой путь из известной точки  Поскольку кенгуру Т является домашним, в качестве его дома можно рассматривать точку
Поскольку кенгуру Т является домашним, в качестве его дома можно рассматривать точку  . Его путь описывается следующей формулой:
. Его путь описывается следующей формулой:
 для
для 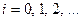 (17.3)
(17.3)
Допустим, что кенгуру Т делает 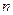 прыжков, а потом останавливается. Требуется определить, сколько прыжков должен сделать кенгуру Т, чтобы поймать кенгуру
прыжков, а потом останавливается. Требуется определить, сколько прыжков должен сделать кенгуру Т, чтобы поймать кенгуру  . После
. После 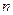 -го прыжка счетчик пути, пройденного кенгуру Т, показывает величину
-го прыжка счетчик пути, пройденного кенгуру Т, показывает величину
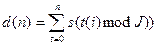 .
.
Используя это значение, можно переписать выражение (17.3) для следов кенгуру Т в следующем виде:
 .
.
Кенгуру  начинает свой путь из неизвестной точки
начинает свой путь из неизвестной точки  . Этой неизвестной точкой считается число
. Этой неизвестной точкой считается число 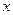 , и именно поэтому кенгуру
, и именно поэтому кенгуру  считается диким. Его путь описывается следующей формулой:
считается диким. Его путь описывается следующей формулой:
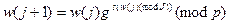 для
для  (17.4)
(17.4)
Счетчик пути, пройденного кенгуру  , регистрирует величину
, регистрирует величину
 .
.
Аналогично выражению (17.3) выражение (17.4) для следов кенгуру  можно переписать в следующем виде:
можно переписать в следующем виде:
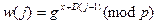 .
.
Очевидно, что следы обоих кенгуру, 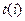 и
и  , представляют собой случайные функции. Первая из этих функций задается в точках
, представляют собой случайные функции. Первая из этих функций задается в точках  , а вторая – в точках
, а вторая – в точках  . Согласно парадоксу дней рождений после
. Согласно парадоксу дней рождений после  прыжков, сделанных кенгуру
прыжков, сделанных кенгуру 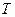 и
и  соответственно, при некоторых значениях
соответственно, при некоторых значениях 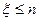 и
и  должна произойти коллизия
должна произойти коллизия 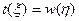 . Именно в этот момент кенгуру
. Именно в этот момент кенгуру 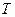 и
и  встретятся в одной точке, т.е. кенгуру
встретятся в одной точке, т.е. кенгуру  попадет в капкан, установленный кенгуру
попадет в капкан, установленный кенгуру 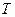 . Итак, кенгуру
. Итак, кенгуру  пойман. Если количество случайных прыжков, сделанных обоими кенгуру, превышает
пойман. Если количество случайных прыжков, сделанных обоими кенгуру, превышает  , вероятность коллизии быстро стремится к 1. В соответствии с формулами (17.3) и (17.4), когда возникает коллизия
, вероятность коллизии быстро стремится к 1. В соответствии с формулами (17.3) и (17.4), когда возникает коллизия 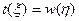 , выполняются равенства
, выполняются равенства 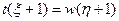 ,
,  ,... и т.д. Иначе говоря, при некоторых числах
,... и т.д. Иначе говоря, при некоторых числах  в конце концов будет выполнено равенство
в конце концов будет выполнено равенство 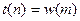 . Поскольку после встречи оба кенгуру продолжают прыгать по одному и тому же пути, ведущему к равенству
. Поскольку после встречи оба кенгуру продолжают прыгать по одному и тому же пути, ведущему к равенству 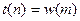 , коллизию
, коллизию 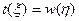 можно интерпретировать как точку, в которой пересекаются две палочки греческой буквы
можно интерпретировать как точку, в которой пересекаются две палочки греческой буквы  (напомним, что кенгуру
(напомним, что кенгуру 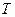 выполняет фиксированное количество прыжков
выполняет фиксированное количество прыжков 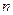 ). По этой причине алгоритм получил название «
). По этой причине алгоритм получил название «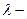 метод».
метод».
После возникновения коллизии выполняется равенство
 .
.
Отсюда следует, что
 .
.
Поскольку оба счетчика показывают величины  и
и  соответственно, величину
соответственно, величину 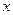 можно вычислить, используя длину пути, пройденного каждым кенгуру. При этом возможна ситуация, когда оба кенгуру пройдут слишком длинный путь до встречи, и поэтому искомая величина индекса может оказаться равной
можно вычислить, используя длину пути, пройденного каждым кенгуру. При этом возможна ситуация, когда оба кенгуру пройдут слишком длинный путь до встречи, и поэтому искомая величина индекса может оказаться равной  , где число
, где число  удовлетворяет равенству
удовлетворяет равенству 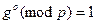 . В этом случае можно считать, что ответом задачи будет число
. В этом случае можно считать, что ответом задачи будет число  .
.
Следует отметить, что алгоритм является вероятностным, т.е. он может не обнаружить коллизию. Несмотря на это, благодаря высокой вероятности обнаружить коллизию вероятность отказа можно сделать достаточно малой. Смещая стартовую точку кенгуру  на известную величину
на известную величину 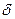 и повторяя алгоритм, после нескольких итераций обязательно обнаружим коллизию.
и повторяя алгоритм, после нескольких итераций обязательно обнаружим коллизию.
Условием, обеспечивающим практическую целесообразность  -алгоритма, является относительная малость величины
-алгоритма, является относительная малость величины  . Следовательно, при
. Следовательно, при  (где
(где 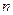 – количество прыжков, сделанных кенгуру
– количество прыжков, сделанных кенгуру 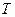 ) алгоритм выполняется за время, которое необходимо для вычисления
) алгоритм выполняется за время, которое необходимо для вычисления 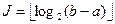 операций возведения в степень по модулю. Требования к памяти компьютера тривиальны: Необходимо хранить лишь
операций возведения в степень по модулю. Требования к памяти компьютера тривиальны: Необходимо хранить лишь 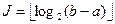 элементов. Временное ограничение, равное
элементов. Временное ограничение, равное  , означает, что данный алгоритм нельзя применять для вычисления больших индексов. Как образно сказал Поллард, кенгуру не может проскакать через весь континент.
, означает, что данный алгоритм нельзя применять для вычисления больших индексов. Как образно сказал Поллард, кенгуру не может проскакать через весь континент.
Раздел восемнадцатый
Кольца и поля. Характеристика. Формула бинома для полей простой характеристики.
Идеалы в кольцах. Факторкольцо.
Определение 1. Пусть на непустом множестве  заданы две бинарные алгебраические операции «
заданы две бинарные алгебраические операции « » и «
» и «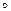 ». Тогда тройка
». Тогда тройка  называется кольцом, если выполнены условия:
называется кольцом, если выполнены условия:
1)  – абелева группа;
– абелева группа;
2) 
 и
и  .
.
Условия 2) называются дистрибутивными законами. Указанные в определении операции традиционно называются соответственно сложением и умножением. В дальнейшем перейдем на традиционную запись. Добавим еще, что если операция умножения ассоциативна, то кольцо называется ассоциативным, а если еще и коммутативным, то – коммутативным. Если по операции умножения существует нейтральный элемент, то говорят о кольце с единицей.
Пример 1.  – коммутативное кольцо с единицей целых чисел.
– коммутативное кольцо с единицей целых чисел.
Пример 2. 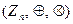 – коммутативное кольцо с единицей классов вычетов по модулю
– коммутативное кольцо с единицей классов вычетов по модулю 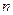 .
.
Пример 3. 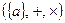 , где
, где  и
и  . Это т.н. нулевое кольцо.
. Это т.н. нулевое кольцо.
Пример 4.  – коммутативное кольцо с единицей многочленов от буквы х над полем Р.
– коммутативное кольцо с единицей многочленов от буквы х над полем Р.
Пример 5.  – ассоциативное кольцо с единицей матриц порядка
– ассоциативное кольцо с единицей матриц порядка 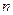 над полем Р.
над полем Р.
Пример 6.  – коммутативное кольцо четных целых чисел (единицы нет).
– коммутативное кольцо четных целых чисел (единицы нет).
Пример 7. 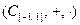 – коммутативное кольцо с единицей вещественных непрерывных функций, заданных на отрезке
– коммутативное кольцо с единицей вещественных непрерывных функций, заданных на отрезке  .
.
Пример 8.  – коммутативное кольцо с единицей целых гауссовых чисел.
– коммутативное кольцо с единицей целых гауссовых чисел.
Простейшие следствия из аксиом кольца выглядят так: для любых 
|
|
|
|
|
Дата добавления: 2014-11-16; Просмотров: 425; Нарушение авторских прав?; Мы поможем в написании вашей работы!