Решаем четыре системы сравнений 3 страница

Чтобы сгенерировать ключ, Алиса, во-вторых, выбирает случайное целое число а, которое имеет порядок q (или примерно такое же большое, как N) и держит его в секрете. Далее, вычисляет точку а В Е и оглашает ее. Боб делает то же самое: выбирает случайное число b и оглашает публично точку b B E. Тайным ключом, который теперь будет использоваться, является Р = аb B E. Оба могут вычислить этот ключ. Например, Алиса знает b B (которую знают все) и знает свое тайное число а. В то время, как третье лицо знает только a B и b B. Таким образом, без решения задачи дискретного логарифмирования – нахождения а, когда известны В и а В (или нахождения b, когда известны В и b B) – не позволяют узнать ab B на основе только а В и b B.

5. Система аналогичная системе ЭльГамала. Это криптосистема с открытым ключом для пересылки сообщения Р . Так же, как и в описанном выше случае системы выработки ключа, начинаем с выбора фиксированного конечного поля F , эллиптической кривой над этим полем и точки В Е (что считается общеизвестным). Не обязательно знать число точек кривой N. Каждый пользователь системы выбирает случайное целое число а, которое держит в тайне от остальных, вычисляет и предает огласке точку а В.

Чтобы выслать Бобу сообщение Р , Алиса выбирает случайное целое число k и пересылает пару точек (kB, P B)), где 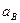В есть открытый ключ Боба. Чтобы прочитать сообщение, Боб умножает первую точку на свой секретный ключ 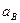и вычитает полученное от другой точки:

Р В) - В) = Р .

Таким образом, Алиса высылает замаскированную точку Р вместе с «подсказкой» k B, достаточной для освобождения от “маски” 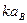В для каждого, кто знает секретный ключ 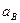. Третьи лица, которые умеют решать задачу дискретного логарифмирования на кривой Е, смогут, очевидно, определить 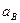из известных всем точек В и 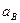В.

6. Выбор кривой и точки. Существует много способов выбора эллиптической кривой и

(в случае систем Диффи-Хеллмана и ЭльГамала) точки В на ней. Рассмотрим вариант с лучайного выбора пары (Е, В). Когда определено большое конечное поле F , можно выбрать одновременно Е и В = (х, y) Е следующим образом. (Положим, что поле имеет характеристику > 3, а значит эллиптическая кривая описана уравнением (11.1) (см. р.11). Выберем, во-первых, три случайных элемента в поле F : x, y и а. 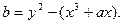Далее, положим Проверяем, что многочлен 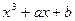не имеет кратных корней, что соответствует условию (Если это условие не выполняется, то выбираем иные x, y и а). В качестве В берем точку 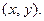Тогда В является точкой эллиптической кривой с уравнением

Если нужно знать число N точек кривой, то существует весьма доступный метод вычисления N. Первым алгоритмом, работающим за полиномиальное время и вычисляющий число точек кривой Е, был открыт R. Schoof’ом. Алгоритм Schoof’а является даже детерминированным. Идея, на которую он опирается, состоит в том, чтобы найти остатки от деления числа точек кривой Е на различные простые числа l, меньшие определенного ограничения. Atkins выработал несколько иной метод, относительно которого нет уверенности в его полиномиальности, однако который работает очень хорошо на практике. В итоге этих усилий стало возможным вычисление порядка произвольной эллиптической кривой над полем F , где q, к примеру, - 50 цифровое число, являющееся степенью простого числа.

Нужно заметить, что хотя использование системы Диффи-Хеллмана или системы ЭльГамала не требуют знать число N, однако на практике требуется, чтобы система была безопасной, а безопасность таких систем зависит от того, имеет ли число N большой простой делитель. Если N является произведением малых простых чисел, то можно использовать метод Силвера-Полига-Хеллмана для решения задачи дискретного логарифмирования. Заметим, что метод Силвера-Полига-Хеллмана переносится на случай задачи о дискретном логарифмировании в произвольной конечной абелевой группе. Таким образом, требуется знать, не является ли число N произведением малых простых чисел, и не ясно, можно ли об этом узнать без вычисления самого числа N.

7. Порядок точки В. Каковы шансы на то, что “случайная” точка В на “случайной” эллиптической кривой является образующим элементом. Как уже говорилось выше, для безопасности вышеописанных криптографических систем не является необходимым то условие, чтобы точка В была образующей. Требуется только, чтобы в циклической подгруппе, порожденной элементом В, задача дискретного логарифмирования была бы трудной для решения. Так будет, т.е. любой из известных методов решения задачи дискретного логарифмирования оказывается слишком медленным, если порядок В будет делиться на очень большое простое число, например, такое, что порядок его величины будет такой же большой, как и у N.

Определенной гарантией того, что выбор В удачен, - и что точка В генерирует эллиптическую кривую – является выбор нашей эллиптической кривой и конечного поля таким образом, чтобы число N точек кривой было простым. Тогда каждая точка В 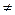О будет порождающей. Далее, если применять описанный выше метод, то для данного поля F следует искать пару (Е, В) до тех пор, пока не найдем такую пару, для которой число точек кривой Е есть число простое (что можно проверить при помощи тестов на простоту).

Замечание. Чтобы группа точек кривой Е mod p для большого простого числа р могла иметь порядок N простым числом, нужно чтобы группа точек кривой Е была группой без кручения, т.е. не имела точек конечного порядка за исключением точки О. В противном случае число N делится на порядок подгруппы кручения.

8. Некоторые задачи.

Задача. Пусть Е будет эллиптическая кривая с уравнением определенная над полем, имеющем р = 751 элементов. (Замена переменных вида 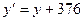приводит это уравнение к виду (11.1) (см. р. 11)). Эта кривая имеет N = 727 точек. Допустим, что единицами открытого текста являются цифры 0-9 и буквы A-Z, которые занумерованы числами от 10 до 35. Пусть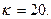

(а) Используя методы, описанные в тексте, записать сообщение «STOP007» в виде

набора семи точек кривой.

(b) Раскодировать набор точек (361, 383), (241, 605), (201, 380), (461, 467), (581, 395) и получить соответствующее сообщение.

(c) Применяя систему аналогичную системе ЭльГамала на основе эллиптических кривых, требуется переслать сообщение из задачи (а), где В = (0, 0). Допустим, что ключом сообщения есть точка (201, 380), а набором случайных чисел k (по одному на каждую единицу текста) есть 386, 209, 118, 589, 312, 483, 335. Какой набор из семи пар точек предстоит переслать?

Раздел тринадцатый

1. Односторонние функции.

Здесь будут рассматриваться функции, областью определения и областью значений которых являются множества слов в некотором алфавите. Не ограничивая общности рассуждений можно считать, что это двоичный алфавит. Тогда одностороннюю функцию 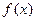можно было бы определить как функцию, удовлетворяющую следующим двум условиям:

1) 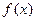эффективно вычислима;

2) любой эффективный алгоритм для большинства аргументов не в состоянии по образу 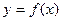найти элемент 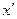такой, что .

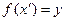Такое пояснение кажется вполне понятным. В качестве примера можно рассмотреть функцию 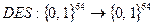. Эта функция биективна, и условие 2) означает, что обратная функция не может быть вычислена эффективно для большинства входов – утверждение, которое является основанием для утверждений о стойкости DES. Математика требует формализации понятий. При этом условия 1) и 2) приобретают асимптотический характер и становятся непригодными для характеризации конкретных конечных функций. Не вдаваясь в подробности строгого определения этого понятия, выскажемся несколько строже:

Определение. Функция f называется односторонней, если

1) вычисляется за полиномиальное время,

2) каждый полиномиальный вероятностный алгоритм на входе 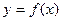для случайного находит какой-либо из прообразов у с вероятностью, которая для достаточно больших n не превосходит 1 /р(n) для любого полинома р(n).

Здесь вероятность распространяется на случайный выбор слова и на случайную последовательность вероятностного алгоритма. Заметим только, функция f еще должна не слишком сильно сжимать данные (т.е. быть «честной»).

Ни для какой конкретной функции не доказано, что она является односторонней. Но многие считаются практически таковыми и с успехом используются. В качестве примеров приведем следующие функции.

(i) Функция умножения: .

Функция определена на парах натуральных чисел х и у с одинаковым количеством значащих двоичных цифр.

(ii) RSA-функция: .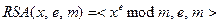

Функция определена для 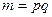, где р и q – различные простые нечетные, для е такого, что 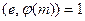и для Z . Для фиксированных е и m является биекцией Z на себя.

(iii) Функция Рабина: .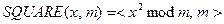

Функция определяется для 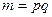, Z , где m – целое Блюма, т.е. р и q – различные простые и .

(iv) Экспоненциальная функция: .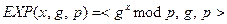

Функция определена для произвольного простого р, первообразного корня g по 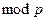и Z .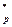

Функции RSA и Рабина являються кандидатами в односторонние функции с секретом. Эти функции, кроме 1) и 2), должны удовлетворять еще одному условию: это условие, являясь секретным, позволяет эффективно обращать функцию. В данном случае таким секретом является знание сомножителей р и q.

Можно привести примеры применения односторонних функций: 1) при организации парольного доступа к базам данных в качестве пароля может храниться в информационной системе значение односторонней функции, так что злоумышленнику, если он добудет пароль 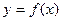из справочника паролей придется решать сложную задачу инвертирования односторонней функции, чтобы найти такое 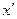, которое бы удовлетворяло условию 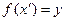и, введя которое, засвидетельствовать о себе как о законном пользователе; 2) при организации защиты конфиденциальности переписки при помощи систем с открытым ключом часто требуется построить большое простое число р, которое менеджер распределения ключей может подобрать так, чтобы иметь возможность доступа к переписке, поэтому можно потребовать, чтобы менеджер вместе с числом р предъявлял бы еще и некоторое х такое, что 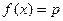для некоторой односторонней функции f;учитывая, что х и f(x) имеют одинаковую длину, то тестирование на простоту числа f(x) не усложняет общую задачу, и при случайном выборе х получаем случайное р.

Существование односторонних функций является необходимым условием стойкости многих типов криптографических схем. В некоторых случаях такой факт устанавливается достаточно просто. Рассмотрим пример. Пусть задана криптосистема с открытым ключом. Алгоритм генерации ключей G в ней общедоступен. Таким образом, всякий желающий может подать ему на вход случайную строку r надлежащей длины и получить пару ключей 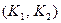. Открытый ключ 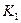публикуется, а секретный ключ 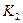и случайная строка r хранятся тайно. Напомним, алгоритмы зашифрования и расшифрования удовлетворяют условию: для любого открытого сообщения m выполняется соотношение 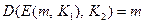. Рассмотрим функцию f такую, что 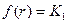. Она вычислима с помощью алгоритма G за полиномиальное время. Покажем, что если f не односторонняя, то система нестойкая. Предположим, что существует полиномиальный вероятностный алгоритм А, который инвертирует f с вероятностью по крайней мере 1/ р(n) для некоторого полинома р, где n – длина ключа 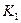. Противник может подать на вход алгоритму А ключ 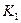и получить с указанной вероятностью некоторое значение 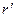из прообраза. Далее противник подает 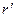на вход алгоритма G и получает пару ключей 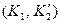. Хотя необязательно совпадает с 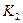, тем не менее, по определению криптосистемы для любого открытого текста m. Поскольку найден с вероятностью по крайней мере 1/ р(n), которая в криптографии не считается пренебрежительно малой, криптосистема нестойкая.

Заметим, что для других криптологических систем подобный результат получается не столь просто. Существование односторонних функций является одним из слабейших условий, которые могут оказаться достаточными для доказательства существования стойких криптологических систем различных типов.

В настоящий момент доказано, что существование односторонних функций является необходимым и достаточным условием существования стойких криптосистем с секретным ключом, а также стойких криптографических протоколов нескольких типов, среди которых протоколы электронной подписи.

2. Хэш-функции.

Хэш-функция представляет собой криптографическую функцию от сообщений произвольной длины, значение которой зависит сложным образом от каждого бита сообщения. Хэш-функция реализуется обычно в виде некоторого итеративного механизма, который позволяет вычислить для сообщения М произвольной длины так называемый хэш-код Н(М) фиксированного размера n (обычно n = 128 бит). Этот код является подобием «слепка» сообщения М. В системах электронной цифровой подписи

вместо подписывания сообщения (например, документов большого объема) используется подписывание соответствующего ему хэш-кода. Этот факт предъявляет к хэш-функциям следующие требования:

1) вычислительно неосуществимо нахождение сообщения М, хэш-код которого был бы равен заданному значению Н;

2) вычислительно неосуществимо нахождение двух сообщений и 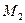, , 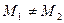с равными значениями хэш-кодов, т.е. удовлетворяющих условию 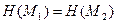(так называемая коллизия).

Невыполнение этих требований грозит возможностью подделки сообщения для выработанного хэш-кода.

Хэш-функция, построенная на базе итеративного механизма, аналитически записывается в виде:

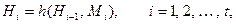
где 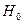– некоторое специфицированное начальное значение, h – некоторая легко вычислимая функция шифрования, 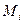– текущий блок сообщения. Сообщение М представляется в виде конкатенации t блоков одинакового размера:

.

Значение 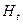принимается за значение хєш-функции, которое можно записать в виде 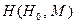, чтобы подчеркнуть зависимость Н от начального параметра .

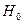Известно, что если какая-либо атака может быть предпринята против базовой функции h, то эта же атака может быть предпринята и против итеративной функции Н, причем сложности атак в обоих случаях одинаковы. Это значит, что необходимо применение криптографически стойких базовых функций. Для построения последних часто используют блочные шифры. Современные блочные шифры являются стойкими к атаке с известным открытым текстом. Поэтому, если использовать блок 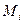в качестве ключа, то по значениям 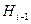(это сообщение является входным для шифрующей функции) и (результат шифрующего преобразования) вычислительно неосуществимо нахождение значения 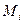, однако возможны атаки, использующие парадокс дней рождения.

Парадокс дней рождения состоит в ответе на следующий вопрос. Какой должна быть численность группы случайно выбранных людей, чтобы с вероятностью ½ в этой группе нашлось два человека с одинаковым днем рождения? Оказывается, что численность такой группы должна составлять примерно 19 человек. Дело в том, что вероятность совпадения дней рождения для случайной пары равна , а в группе из n человек имеется 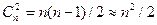разных пар. Вероятность того, что хотя бы у одной из этих пар будет иметь место совпадение дней рождения, составляет 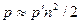, откуда для р = ½ получаем (более точно см. р.17).

Покажем, что использование 64-битового хэш-кода недопустимо, поскольку в этом случае возможна следующая атака. Выберем достаточно длинное сообщение М и вычислим для него следующие промежуточных значений хэш-функции:

.

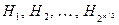В соответствии с парадоксом дней рождения с вероятностью ½ среди этих значений найдутся два равных. Пусть это будут и 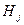. Удалив из М блоки 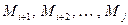, получаем новое сообщение 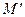, которое имеет значение хэш-функции, равное значению хэш-функции сообщения М. Легко видеть, что сложность этой атаки составляет около

операций шифрования n -битовых блоков. В случае 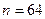получаем шифрований.

Важным применением хэш-функций является контроль целостности информации, например, программ и данных в ЭВМ. В случае, когда речь идет о контроле целостности больших объемов информации, становится актуальной проблема разработки скоростных хэш-функций.

В качестве примера одной из известных хэш-функций укажем на SHA, построенную в США и используемую, в частности, в американском стандарте цифровой подписи DSA (или DSS).

Раздел четырнадцатый

1. Псевдослучайные генераторы.

В практической криптографии потребность получения случайных последовательностей весьма велика. Они требуются для работы вероятностных алгоритмов и в некоторых других случаях. Напомним, что случайной последовательностью битов длины n называют случайную величину, которая принимает каждое значение из множества 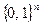с вероятностью 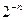. Для малых n такую последовательность можно создать подкидыванием монеты. В случае же больших n эта задача может оказаться сложной и для ЭВМ.

Рассмотрим следующую задачу. Пусть имеется возможность генерировать случайную двоичную последовательность длины n. Спрашивается, можно ли ее расширить до случайной в определенном смысле последовательности длины 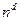, где d – константа? Сам термин «расширить» означает получить из имеющейся с помощью детерминированного алгоритма. Ясно, что в результате такого «расширения» нельзя получить истинно случайную последовательность длины 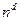. Однако хотелось бы получить хотя бы псевдослучайную последовательность длины 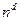, т.е. такую, которая бы походила на случайную.

Определение. Ансамблем называется последовательность случайных величин , , которые принимают значения во множестве двоичных слов.

Определение. Ансамбл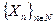и и 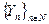называются неразличимыми за полиномиальное время, если для любого полиномиального вероятностного алгоритма А выполняется

,

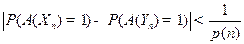для любого полинома р(n) и достаточно больших n. Здесь 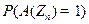означает вероятность того, что алгоритм, получив на входе случайную величину , дает на выходе 1. Вероятность берется как по распределению , так и по распределению случайной последовательности вероятностного алгоритма А.

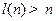Определение. Пусть – функция такая, что . Генератором с расширением l называется полиномиальный детерминированный алгоритм G, который двоичную последовательность превращает в последовательность .

Из соображений технического удобства договоримся, что генератор G может давать отказ, и тогда G (x) может быть не определена.

Остается договориться, какой генератор заслуживает быть названным генератором псевдослучайных последовательностей. Здесь главной чертой такого генератора 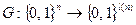должно быть то, что случайную величину G (x), где случайное , никаким полиномиальным вероятностным алгоритмом нельзя отличить от случайной величины, равномерно распределенной на .

Дата добавления: 2014-11-16