Пример 5. Таблица 5.13.- Данные о валовом сборе зерновых культур, млн.т

Таблица 5.13.- Данные о валовом сборе зерновых культур, млн.т..

Годы	Валовый сбор зерна, млн. т.	Сумма по пяти уровням, Σ У	Скользящая средняя по 5 уровням, Σ У: 5
	4,3	-	-
	4,5	-	-
	4,3	-	4,72
	5,2	-	5,00
	5,3	23,6	5,30
	5,7		5,64
	6,0	26,5	5,78
	6,0	28,2	5,86
	5,9	28,9	6,10
	5,7	29,3	6,32
	6,9	30,5	6,58
	7,1	31,6	6,94
	7,3	32,9	7,48
	7,7	34,7	7,68
	8,4	37,4	7,92
	7,9	38,4	8,22
	8,3	39,6	8,38
	8,8	41,1	8,54
	8,5	41,9	8,94
	9,2	42,7	9,18
	9,9	44,7	9,30
	9,6		-
	9,3	46,5	-

Для вычисления средних, суммируем первые пять показателей соответственно за 1985-89 гг.

4,3+4,5+4,3+5,2+5,3 =23,6

Среднее значение равно 4,72

Затем опускаемся на один уровень ниже и суммируем данные за 1986- 1990 гг.

4,5+4,3+5,2+5,3+5,7 = 25 или 23,6 - 4,3 + 5,7 = 25

На рис. 5.1 показан график, построенный по данным о валовом сборе зерна в стране за ряд лет наблюдения и по расчетным данным, представленным в таблице 5.13.

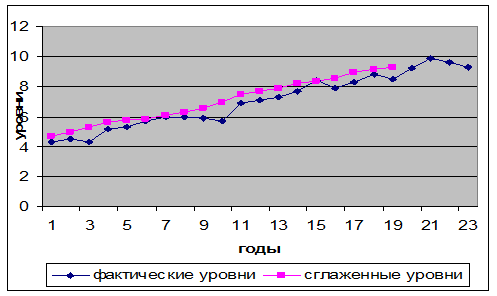
Рис. 5.1. Валовый сбор зерновых.

Наиболее совершенным способом определения тенденции развития в ряду динамики является метод аналитического выравнивания. При этом методе исходные уровни ряда динамики 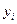заменяются теоретическими или расчетными , которые представляют из себя некоторую достаточно простую математическую функцию времени, выражающую общую тенденцию развития ряда динамики. Чаще всего в качестве такой функции выбирают прямую, параболу, экспоненту и др.

Например, ,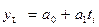

где 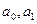- коэффициенты, определяемые в методе аналитического выравнивания;

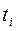- моменты времени, для которых были получены исходные и соответствующие теоретические уровни ряда динамики, образующие прямую, определяемую коэффициентами .

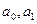Расчет коэффициентов 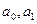ведется на основе метода наименьших квадратов:

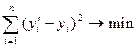
Если вместо 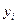подставить 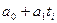(или соответствующее выражение для других математических функций), получим:

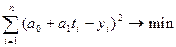
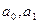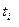Это функция двух переменных (все и 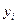известны), которая при определенных 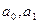достигает минимума. Из этого выражения на основе знаний, полученных в курсе высшей математики об экстремуме функций n переменных, получают значения коэффициентов .

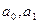Для прямой:

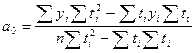
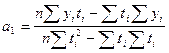
где n — число моментов времени, для которых были получены исходные уровни ряда .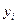

Если вместо абсолютного времени 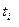выбрать условное время таким образом, чтобы 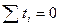, то записанные выражения для определения 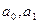упрощаются:

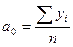
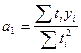
Дата добавления: 2014-11-16