Примеры решения задач. Реальные газы, жидкости и твердые тела

Реальные газы, жидкости и твердые тела

● Уравнение состояния реальных газов (уравнение Ван-дер-Ваальса) для произвольной массы газа

,

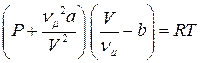где a и b – постоянные Ван-дер-Ваальса, различные для различных газов.

● Внутреннее давление, обусловленное силами взаимодействия молекул

,

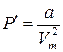где V_m – молярный объем.

● Внутренняя энергия реального газа

.

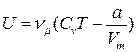● Поверхностное натяжение

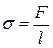, или ,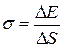

где F – сила поверхностного натяжения, действующая на контур 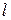, ограничивающий поверхность жидкости; 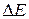- поверхностная энергия, связанная с площадью 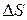поверхности пленки.

● Высота подъема жидкости в капиллярной трубке

,

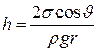где θ – краевой угол; r – радиус капилляра; ρ – плотность жидкости; g – ускорение свободного падения.

● Закон Дюлонга и Пти

,

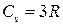где С_v – молярная (атомная) теплоемкость химически простых твердых тел.

Задача 1. Движение материальной точки задано уравнением 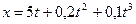(м). Определить скорость точки в моменты времени t₁=2 с и

t₂=4 с, а также среднюю скорость в интервале времени от t₁ до t₂.

Решение:

Точка прямолинейно движется вдоль оси OX. Модуль мгновенной скорости в этом случае

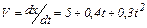(м/с).

Найдем V₁ и V₂:

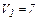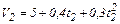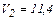, м/с;

, м/с.

Средняя скорость

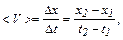
где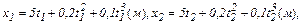

м/с.

Ответ: V₁=7 м/с, V₂=11,4 м/с, м/с

Задача 2. Тело массой 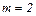кг движется по вертикальной стене. Сила 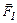действует под углом a = 30⁰ к вертикали. Коэффициент трения 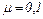. Найти величину силы 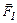, если ускорение тела направлено вверх и равно a = 2 м/с² .

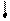Решение:

На тело действуют четыре силы: сила 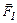, сила тяжести 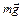, сила реакции опоры 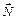и сила трения 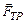. Покажем эти силы на рисунке.

Запишем II закон Ньютона в виде

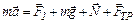. (1) Ось OY направим вертикально вверх, ось OX – перпендикулярно стене. В проекциях на оси координат уравнение (1) примет вид

OХ: 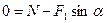(2)

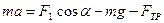OY: . (3)

Сила трения скольжения

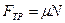. (4)

Используя (2) и (4), перепишем (3):

.

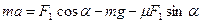Отсюда

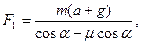
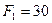Н.

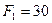Ответ: Н.

Задача 3. Частица массой m₁, имеющая скорость V₂, налетела на покоящийся шар массой m₂ и отскочила от него со скоростью U₁ под прямым углом к направлению первоначального движения. Какова скорость U₂ шара после соударения? Считать удар центральным.

Решение:

Используя закон сохранения импульса, получим

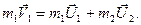
На рисунке покажем импульсы тел.

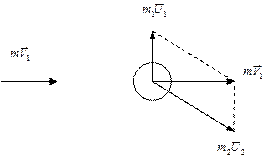Модуль импульса шара найдём, используя теорему Пифагора:

,

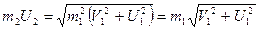отсюда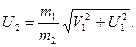

Ответ: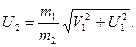

Задача 4. Шар массой M висит на нити длиной l. В шар попадает горизонтально летящая пуля и застревает в нём. С какой скоростью V₀ должна лететь пуля, чтобы в результате попадания пули шар мог сделать на нити полный оборот в вертикальной плоскости? Размерами шара пренебречь. В верхней точке сила натяжения нити равна нулю. Масса пули m.

Решение:

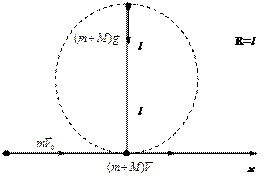Обозначим: V – скорость шара с пулей сразу после неупругого соударения, U – скорость шара с пулей в верхней точке.

В проекциях на ось OX закон сохранения импульса имеет вид

mV₀ = (m + M) V. (1)

Выберем нулевой уровень отсчёта потенциальной энергии, совпадающий с осью OX.

В нижнем положении шар с пулей обладает только кинетической энергией 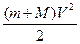; в верхней точке - кинетической 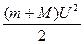и потенциальной (m+M)gh энергиями, где h = 2R =2l.

Закон сохранения механической энергии запишем в виде

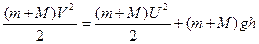. (2)

После преобразований

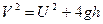. (2¢)

В верхней точке на шар с пулей действует сила тяжести, по условию задачи сила натяжения нити равна нулю. Используем II закон Ньютона:

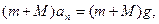(3)

где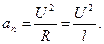

Из уравнения (1) выразим V₀:

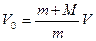_. (4)

Из уравнения (3)

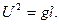(5)

Подставив (5) в (2¢), получим

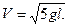
Найдем V₀, вернувшись к (4)

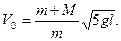
Ответ: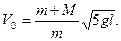

Задача 5. По наклонной плоскости, образующей угол a с горизонтом, скатывается без скольжения 1) сплошной однородный диск, 2) шар. Определить линейное ускорение их центров. Предварительно вывести общую формулу.

Решение:

Тело участвует в сложном движении:

1)поступательно движется вниз по наклонной плоскости;

2) вращается вокруг оси, проходящей через центр тяжести.

На рисунке покажем силы, действующие на тело.

Для поступательного движения запишем II закон Ньютона в проекциях на ось OX.

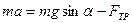. (1)

Для вращательного движения используем закон

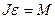, (2)

где 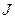- момент инерции, 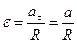- угловое ускорение.

Момент силы 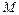создает сила трения, плечо которой равно R, две другие силы не создают вращающего момента.

.

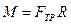Перепишем (2):

.

Выразим силу трения из (3) и подставим в (1):

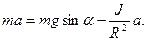
Отсюда

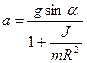. (4)

Зная моменты инерции диска и шара

,

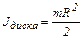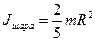
найдем ускорения диска и шара

,

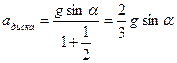Ответ: ,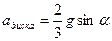

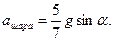
Задача 6. Две частицы движутся навстречу друг другу со скоростями 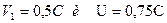. Найти их относительную скорость.

Решение:

Согласно теореме сложения скоростей в теории относительности,

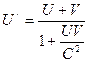, где 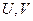-скорости первой и второй частицы; 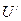- их относительная скорость: С- скорость света в вакууме.

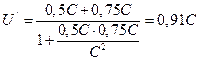
Это означает, что, во первых, ни в какой инерциальной системе отсчёта скорость процесса не может превзойти скорость света, и, во вторых, скорость распространения света в вакууме абсолютна.

Ответ: 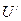= 0,91С.

Задача 7. В баллоне объёмом 20 л находится аргон под давлением 1,0 Мпа и температуре 300 К. После того как из баллона было взято 20,0 г аргона, температура в баллоне понизилась до 280 К. Определить давление газа, оставшегося в баллоне.

Решение:

Для решения задачи воспользуемся уравнением состояния идеального газа, применив его к начальному и конечному состояниям газа:

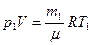, (1)

. (2)

Из уравнений (1) и (2) выразим m₁ и m₂ и найдём их разность:

,

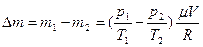откуда находим

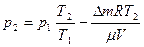. (3)

Проверку решения проведем по размерности физических величин. В правую часть вместо символов величин подставим их единицы измерения. В правой части два слагаемых. Первое из них имеет размерность давления, так как состоит из двух множителей, первый из которых – давление, а второй – безразмерный. Проверим второе слагаемое:

.

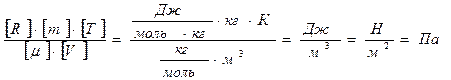
Вычисления произведём по формуле (3) с учётом, что для аргона 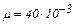кг/моль.

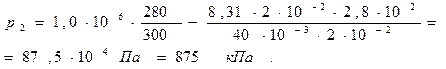
Ответ: 875 кПа

Задача 8. Во сколько раз следует изотермически увеличить объем идеального газа в количестве 3 моль, чтобы его энтропия увеличилась на

25 Дж/К?

Решение:

Для обратимого процесса ,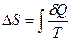

где .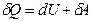

Так как процесс изотермический, то для идеального газа 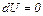, а элементарная работа равна

.

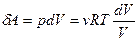Изменение энтропии для изотермического процесса будет равно

.

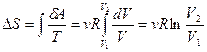Из последнего соотношения находим

.

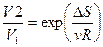Показатель экспоненты – величина безразмерная.

Вычисления: .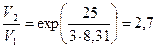

Ответ: .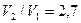

Дата добавления: 2014-11-16