Механические и электромагнитные колебания

КОЛЕБАНИЯ. ВОЛНЫ. ОПТИКА

Основные формулы

● Уравнение гармонических колебаний

х = А (ω₀ t + φ₀),

где s – смещение колеблющейся величины от положения равновесия; Α – амплитуда колебаний; ω₀ = 2 π / T = 2 πν – круговая (циклическая) частота;

ν = 1/ T – частота; T – период колебаний; (ω₀t+φ₀) – фаза колебаний; φ ₀ – начальная фаза.

● Скорость и ускорение точки, совершающей гармонические колебания,

;

.

● Кинетическая энергия колеблющейся точки массой m

● Потенциальная энергия

● Полная энергия

.

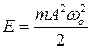● Дифференциальное уравнение гармонических колебаний материальной

точки массой m

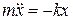, или ,

где k – коэффициент упругости (k = ω₀²m).

● Период колебаний пружинного маятника

,

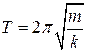где m – масса пружинного маятника; k - жесткость пружины.

● Период колебаний физического маятника

,

где Ј – момент инерции маятника относительно оси колебаний;

l – расстояние между точкой подвеса и центром масс маятника;

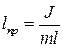– приведенная длина физического маятника; g – ускорение свободного падения.

● Период колебаний математического маятника

,

где l – длина маятника.

● Формула Томсона, устанавливающая связь между периодом Т собсвен-

ных колебаний в контуре без активного сопротивления и индуктивностью L и емкостью контура С,

Т = 2 π .

● Дифференциальное уравнение свободных гармонических колебаний

заряда в контуре и его решение:

; ,

где - амплитуда колебаний заряда; - собственная частота контура.

● Дифференциальное уравнение свободных затухающих колебаний

линейной системы и его решение:

; ,

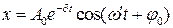где х – колеблющаяся величина, описывающая физический процесс;

δ – коэффициент затухания ( в случае механических колебаний и

в случае электромагнитных колебаний); ω₀ – циклическая частота свободных незатухающих колебаний той же колебательной системы;

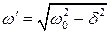- частота затухающих колебаний; 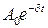– амплитуда затухающих колебаний.

● Декремент затухания

,

где А(t) и A(t+T) – амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период.

● Логарифмический декремент затухания

,

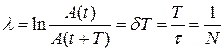где τ = 1/ δ – время релаксации; N – число колебаний, совершаемых за время уменьшения амплитуды в е раз.

● Добротность колебательной системы

.

● Дифференциальное уравнение вынужденных колебаний и его решение

для установившихся колебаний:

, ,

где х– колеблющаяся величина, описывающая физический процесс

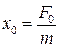( в случае механических колебаний, 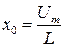в случае электромагнитных колебаний);

; .

● Резонансная частота и резонансная амплитуда

; .

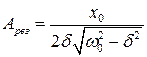● Сдвиг фаз между напряжением и силой тока

.

Дата добавления: 2014-11-16