Магнитные свойства вещества

● Связь орбитального магнитного 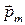и орбитального механического

моментов электрона

,

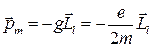где – гиромагнитное отношение орбитальных моментов.

● Намагниченность

,

где – магнитный момент магнетика, равный векторной сумме магнитных моментов отдельных молекул.

● Связь между намагниченностью и напряженностью магнитного поля

,

где χ – магнитная восприимчивость вещества.

● Связь между векторами

,

где μ₀ – магнитная постоянная.

● Связь между магнитной проницаемостью и магнитной восприимчи-

востью вещества

μ = 1 + χ.

● Закон полного тока для магнитного поля в веществе (теорема о циркуляции вектора )

,

где 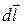– вектор элементарной длины контура, направленный вдоль обхода контура; B_l – составляющая вектора в направлении касательной контура γ произвольной формы; I и I' – соответственно алгебраические суммы макротоков (токов проводимости) и микротоков (молекулярных токов), охватываемых заданным контуром.

● Теорема о циркуляции вектора напряженности магнитного поля

,

где I – алгебраическая сумма токов проводимости, охватываемых контуром γ.

Примеры решения задач

Задача 1. Нить в форме полуокружности заряжена равномерно с линейной плотностью t. С помощью принципа суперпозиции найдите значение напряженности и потенциала в центре соответствующей окружности.

Решение:

Рассмотрим элемент нити dl, несущий заряд dq = t×dl. К нему применимы формулы, определяющие поле точечного заряда, т.е.

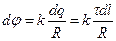и .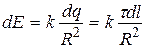

Т.к. каждый элемент в силу симметрии формы нити имеет симметричный участок (см. рисунок) вектор напряженности поля которого симметричен вектору относительно указанной на рисунке оси симметрии, то суммарная напряженность поля будет направлена по оси симметрии и равна сумме проекций векторов на эту ось (проекции на перпендикулярное к этой оси направление взаимно компенсируются).

В соответствии с формулами 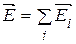, получим значение потенциала поля нити:

.

Для нахождения напряженности потребуется взять в качестве переменной интегрирования не элемент длины, а элементарный угол da:

,

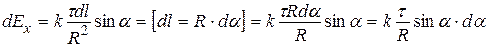тогда

.

Полученные значения относятся лишь к одному частному случаю (к единственной точке – центру).

Ответ: , .

Задача 2. Протон, движущийся со скоростью v ₀=100 км/с, влетает в электрическое поле с напряженностью Е =50 В/м в направлении, противоположном направлению силовых линий поля. Какую разность потенциалов пройдет протон до полной остановки? Через сколько микросекунд скорость протона станет равной нулю? Отношение заряда протона к его массе равно =10⁸ Кл/кг.

Решение:

Протон – частица, несущая положительный заряд. Со стороны электрического поля на нее действует сила в направлении силовых линий. В данном случае эта сила направлена противоположно скорости частицы, поэтому скорость протона будет уменьшаться по мере его движения в поле до нуля, а затем начнется движение в противоположном начальному направлении. В этом усматривается аналогия с движением тела, брошенного вверх в поле тяготения Земли. Электростатическое поле, как и гравитационное, потенциально: заряженная частица обладает в этом поле потенциальной энергией.

При движении протона в электростатическом поле на него не действуют непотенциальные силы, поэтому выполняется закон сохранения полной механической энергии. Отсюда следует, что в положениях 1 и 2 суммы кинетической и потенциальной энергии протона равны между собой:

,

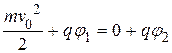Þ .

А искомая разность потенциалов равна

.

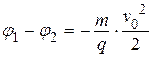Знак «–» означает. что протон движется в сторону большего потенциала.

Рассмотренное выше рассуждение широко применяется при использовании понятия ускоряющей разности потенциалов.

Заметим, что физический смысл имеет не само значение потенциала, а разность потенциалов между двумя точками, что и отражено в приведенных выше рассуждениях. А значение потенциала в некоторой точке определяется, в соответствии с этим, лишь относительно другой точки, выбранной в качестве нулевой (значение потенциала в которой условно принимается равным нулю).

Для ответа на второй вопрос задачи рассмотрим равнозамедленное движение протона под действием электрической силы . По второму закону Ньютона для протона ускорение равно

.

Зависимость модуля скорости от времени при равнозамедленном движении имеет вид

,

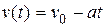тогда при . Подставляя выражение для ускорения, получаем искомое время:

.

Вычисления:

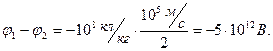
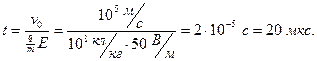
Ответ: , .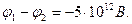

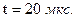Задача 3. Батарею из двух конденсаторов ёмкостью 400 и 500 пФ. Соединили последовательно и включили в сеть с напряжением 220 В. Потом батарею отключили от сети, конденсаторы разъединили и соединили параллельно обкладками, имеющими одноимённые заряды. Каким будет напряжение на зажимах полученной батареи.

Решение:

У последовательно соединённых конденсаторов заряды на обкладках равны по модулю 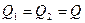и заряд батареи равен заряду одного конденсатора. Ёмкость батареи последовательно соединённых конденсаторов определяется по формуле 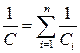. Для батареи из двух конденсаторов , а их заряд

. (1)

При отключении конденсаторов от сети их заряд сохраняется. У параллельно соединённых конденсаторов заряд батареи равен сумме зарядов конденсаторов , а ёмкость – сумме емкостей .

Напряжение на зажимах батареи из двух параллельно соединённых конденсаторов

(2)

Подставляя (1) в (2), получаем

Ответ: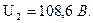

Задача 4. Сила тока в проводнике сопротивлением R =10 Ом за время D t =50 с равномерно возрастает от I ₁=5 А до I ₂=10 А. Определите: 1) заряд, протекший через поперечное сечение проводника за указанное время; 2) количество теплоты, выделившееся за это время в проводнике.

Решение:

Из кинематики известно, что в случае равномерного возрастания скорости (равноускоренное движение) средняя на участке скорость равна среднему арифметическому от значений скорости в начале и в конце рассматриваемого участка движения. По аналогии найдем в данном случае среднее значение силы тока:

(А).

Тогда также, как, зная среднюю скорость, находится весь пройденный путь, суммарный прошедший через поперечное сечение заряд будет равен

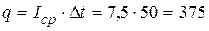(Кл).

Будем теперь искать количество теплоты, выделившееся за это время в проводнике.

Прежде всего, найдем искомое значение в соответствии с законом Джоуля-Ленца:

,

Нетрудно видеть, что сила тока меняется по закону

.

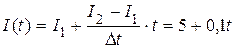Подставляем и вычисляем

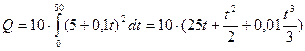=29,17 (кДж).

Ответ: Q=29,17кДж.

Задача 5. По круговому витку радиуса r =0,1 м циркулирует ток силы I =1 А. Найдите магнитную индукцию В: а) в центре витка; б) на оси витка на расстоянии b =0,1 м от его центра.

Решение:

а) Магнитная индукция элементарного поля в центре витка по закону Био-Савара-Лапласа равна

,

т.е. вектор 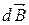перпендикулярен плоскости рисунка (см. рис. а) и численно равен

.

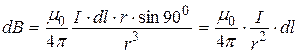Учитывая, что все элементы тока на круговом витке одинаково расположены по отношению к центру витка, получим

.

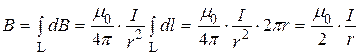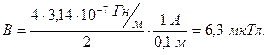
б) Магнитная индукция элементарного поля на оси витка по закону Био-Савара-Лапласа равна

.

Отсюда ясно (по определению векторного произведения), что вектор перпендикулярен плоскости, образованной векторами и , т.е. для каждого элемента тока вдоль витка имеет свое направление. Совокупность векторов образует коническую поверхность, ось которой совпадает с осью витка (рис.б)). Векторная сумма всех с учетом симметрии будет направлена по оси витка и численно равна сумме проекций отдельных на эту ось:

.

Учитывая, что все элементы тока на круговом витке равноценно расположены по отношению к центру витка, получим

.

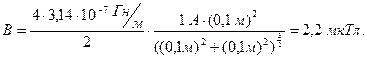
Ответ: а) В=6,3 мкТл, в) В=2,2 мкТл.

Задача 6. Согласно теории Бора, электрон в атоме водорода движется вокруг ядра по круговой орбите радиусом r =52,8 пм. Определите магнитную индукцию В поля, создаваемого электроном в центре круговой орбиты.

Решение:

Будем находить величину магнитной индукции поля, созданного движущимся электрическим зарядом, исходя из формулы

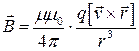
В скалярном виде для движущегося электрона в вакууме

,

где скорость движения электрона найдем из второго закона Ньютона, считая, что центростремительное ускорение электрону сообщает кулоновская сила его взаимодействия с положительно заряженным ядром:

Þ ,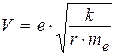

тогда искомая величина равна

.

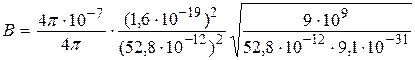=12,568 (Тл).

Ответ: В=12,568 Тл.

Задача 7. Тонкий медный проводник массой 1 г согнут в виде квадрата и концы его замкнуты. Квадрат помещен в однородное магнитное поле (В =0,1 Тл) так, что плоскость его перпендикулярна линиям индукции поля. Определите количество электричества q, которое протечет по проводнику, если квадрат, потянув за противоположные вершины, вытянуть в линию.

Решение:

При вытягивании квадрата в линию меняется магнитный поток сквозь ограниченную им площадь с начальной величины

,

где – площадь квадрата со стороной а, до нуля. При этом по закону электромагнитной индукции в замкнутом контуре возникает ЭДС индукции, среднее значение которой равно

.

где 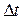- время вытягивания квадрата в линию. Получаем:

.

Далее по закону Ома в контуре возникнет ток, среднее значение которого равно

,

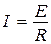где R – сопротивление проводника квадрата, которое найдем, зная материал и размеры линейного проводника:

,

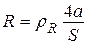где 4 а – периметр квадрата, S – площадь поперечного сечения проводника, 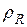- удельное сопротивление меди.

Наконец, исходя из определения силы тока найдем суммарный заряд, прошедший по проводнику:

.

Осталось связать линейные размеры квадрата и площадь поперечного сечения проводника с массой меди и ее плотностью :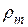

Þ .

Получаем:

.

Вычислим

(Кл)

Ответ: Q=0,041 Кл.

Задача 8. Плоский квадратный контур со стороной =10 см, по которому течет ток =100 А, свободно установился в однородном магнитном поле (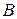 =1 Тл). Определить работу , совершаемую внешними силами при повороте контура относительно оси, проходящей через середину его противоположных сторон, на угол: 1) =90⁰; 2) 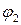=3⁰. При повороте контура сила тока в нем поддерживается неизменной.

Решение:

Как известно, на контур с током в магнитном поле действует момент сил:

.

По условию задачи, в начальном положении контур свободно установился в магнитном поле. При этом момент сил равен нулю (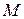 =0), а значит 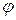=0, т.е. векторы 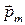и совпадают по направлению.

Если внешние силы выведут контур из положения равновесия, то возникший момент сил, будет стремиться возвратить контур в исходное положение. Против этого момента и будет совершаться работа внешними силами. Так как момент сил переменный (зависит от угла поворота 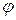), то для подсчета работы применим формулу работы в дифференциальной форме:

.

Подставив сюда выражение 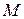и учтя, что 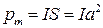, где - сила тока в контуре; 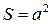- площадь контура, получим:

.

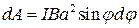Взяв интеграл от этого выражения, найдем работу при повороте на конечный угол:

.

Выразим угол 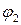в радианах. После подстановки числовых значений величин найдем:

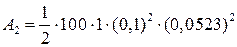Дж = 1,37×10^-3 Дж = 1,37 мДж.

Дата добавления: 2014-11-16