Примеры решения задач. Пример 1.От двух когерентных источников S1 и S2 (l = 0,8 мкм) лучи попадают на экран

Пример 1. От двух когерентных источников S₁ и S₂ (l = 0,8 мкм) лучи попадают на экран. На экране наблю­дается интерференционная картина. Когда на пути одно­го из лучей перпендикулярно ему поместили мыльную пленку (n = 1,33), интерференционная картина изменилась на противоположную. При какой наименьшей толщине d_min пленки это возможно?

Р е ш е н и е. Изменение интерференционной картины на противоположную означает, что на тех участках экрана, где наблюдались интерференционные максимумы, стали наблюдаться интерференционные минимумы. Такой сдвиг интерференционной картины возможен при изменении оптической разности хода пучков световых волн на нечетное число половин длин волн, т. е.

(1)

где D₁ - оптическая разность хода пучков световых волн до внесения пленки; D₂ - оптическая разность хода тех же пучков после внесения пленки; k = 0, ±1, ±2,....

Наименьшей толщине d_min пленки соответствует k = 0. При этом формула (1) примет вид

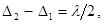(2)

Выразим оптические разности хода D₂ и D₁. Из рис. 21 следует:

Подставим выражения D₁ и D₂ в формулу (2):

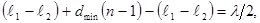
или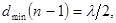

Отсюда

Произведем вычисления:

Пример 2. На стеклянный клин с малым углом нор­мально к его грани падает параллельный пучок лучей монохроматического света с длиной волны l = 0,6 мкм. Число m возникающих при этом интерференционных полос, приходящихся на отрезок клина длиной l, равно 10. Определить угол a клина.

Р е ш е н и е. Параллельный пучок света, падая нормально к грани клина, отражается как от верхней, так и от нижней грани. Эти отраженные пучки света когерентны. Поэтому на поверхности клина будут наблюдаться интерференцион­ные полосы. Так как угол клина мал, то отраженные пуч­ки 1и 2света (рис. 22) будут практически параллельны.

Темные полосы видны на тех участках клина, для которых разность хода лучей кратна нечетному числу половин длин волн:

(1)

Разность хода D двух волн складывается из разности оптических длин путей этих волн 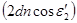и половины длины волны (l/2). Величина l/2представляет собой добавочную разность хода, возникающую при отражении световой волны 1от оптически более плотной среды. Подставляя в формулу (1) разность хода D световых волн, получаем

(2)

где n - показатель преломления стекла (n = 1,5); d_k - толщина клина в том месте, где наблюдается темная полоса, соответствующая номеру k; e¢₂ - угол прелом­ления.

Согласно условию, угол падения равен нулю; следо­вательно, и угол преломления e¢₂ равен нулю, а cose¢₂ =1. Раскрыв скобки в правой части равенства (2), после упрощения получим

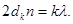(3)

Пусть произвольной темной полосе k-го номера соот­ветствует толщина d_kклина, а темной полосе k+m-го номера - толщина d_k+m клина. Тогда (рис. 60), учиты­вая, что m полос укладывается на расстоянии l, найдем:

(4)

Выразим из (3) d_kи d_k+m и подставим их в формулу (4). Затем, учитывая, что sina = a (из-за малости угла a), получим

Подставляя значения физических величин, найдем

Выразим a в секундах. Для этого можно восполь­зоваться соотношением между радианом и секундой:

1 рад = 206 265"»2,06 ×10⁵". Тогда a = 2×10^-4×2,06×10⁵" = 41,2".

Пример 3. На дифракционную решетку в направле­нии нормали к ее поверхности падает монохроматиче­ский свет. Период решетки d=2мкм. Определить наи­больший порядок дифракционного максимума, который дает эта решетка в случае красного (l₂ = 0,7 мкм) и в случае фиолетового (l₂ = 0,41 мкм) света.

Р е ш е и и е. Из формулы, определяющей положение главных максимумов дифракционной решетки, найдем порядок m дифракционного максимума:

(1)

где d- период решетки; j - угол дифракции; l- длина волны монохроматического света. Так как sinj не может быть больше 1, то число mне может быть больше d/l, т.е.

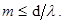(2)

Подставив в формулу (2) значения величин, получим:

(для красных лучей);

(для фиолетовых лучей).

Если учесть, что порядок максимумов является це­лым числом, то для красного света m_max = 2 и для фиоле­тового m_max = 4.

Пример 4. Пучок естественного света падает на полированную поверхность стеклянной пластины, погруженной в жидкость. Отраженный от пластины пучок света образует угол j = 97° с падающим пучком (рис. 23). Определить показатель преломления n₁, жидкости, если отраженный свет максимально поляризован.

Р е ш е н и е. Согласно за­кону Брюстера, пучок света, отраженный от диэлектрика, максимально поляризован в том случае, если тангенс угла падения численно равен относительному показателю пре­ломления tge = n₂₁, где n₂₁ - показатель преломления вто­рой среды (стекла) относительно первой (жидкости).

Относительный показатель преломления равен отно­шению абсолютных показателей преломления. Следова­тельно,

tge = n₂/n₁.

Так как угол падения равен углу отражения, то e = j/2 и, следовательно, tg(j/2) = n₂/n₁, откуда

Произведем вычисления:

Пример 5. Два николя N₁, и N₂расположены так, что угол между их плоскостями пропускания составляет a = 60°. Определить, во сколько раз уменьшится интен­сивность I₀ естественного света: 1) при прохождении через один николь N); 2) при прохождении через оба николя. Коэффициент поглощения света в николе k= 0,05. Потери на отражение света не учитывать.

Р е ш е н и е 1.
Естественный свет, падая на грань призмы николя (рис. 24), расщепляется вследствие двойного лучепреломления на два пучка: обыкновенный и необыкновенный. Оба пучка одинаковы по интенсив­ности и полностью поляризованы. Плоскость колебаний необыкновенного пучка лежит в плоскости чертежа (плоскость главного сечения). Плоскость колебанийобыкновенного пучка перпендикулярна плоскости черте­жа. Обыкновенный пучок света (о) вследствие полного отражения от границы АВ отбрасывается на зачерненную поверхность призмы и поглощается ею. Необыкновенный пучок (е)проходит через призму, уменьшая свою интен­сивность вследствие поглощения. Таким образом, интен­сивность света, прошедшего через первую призму,

Относительное уменьшение интенсивности света полу­чим, разделив интенсивность I₀естественного света, падающего на первый николь, на интенсивность I₁поля­ризованного света:

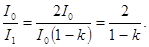(1)

Произведем вычисления:

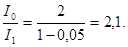
Таким образом, интенсивность уменьшается в 2,1 раза.

2. Плоскополяризованный пучок света интенсивности I₁падает на второй николь N₂и также расщепляется на два пучка различной интенсивности: обыкновенный и необыкновенный. Обыкновенный пучок полностью погло­щается призмой, поэтому интенсивность его нас не интересует. Интенсивность I₂ необыкновенного пучка, вышедшего из призмы N₂,определяется законом Малюса (без учета поглощения света во втором николе):

где a - угол между плоскостью колебаний в поляризо­ванном пучке и плоскостью пропускания николя N₂.

Учитывая потери интенсивности на поглощение во втором николе, получаем

Искомое уменьшение интенсивности при прохождении света через оба никеля найдем, разделив интенсив­ность I₀естественного света на интенсивность I₂света, прошедшего систему из двух николей:

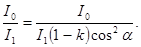
Заменяя отношение I₀/I₁его выражением по форму­ле (1), получаем

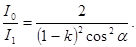
Произведем вычисления: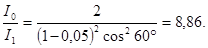

Таким образом, после прохождения света через два николя интенсивность его уменьшится в 8,86 раза.

Пример 6. Плоскополяризованный монохроматический пучок света падает на поляроид и полностью им гасится. Когда на пути пучка поместили кварцевую пластину, интенсивность Iпучка света после поляроида стала рав­на половине интенсивности пучка, падающего на поля­роид. Определить минимальную толщину кварцевой пластины. Поглощением и отражением света поляроидом пренебречь, постоянную вращения в кварца принять рав­ной 48,9 град/мм.

Р е ш е и и е. Полное гашение света поляроидом озна­чает, что плоскость пропускания поляроида (штриховая линия на рис. 25) перпендикулярна плоскости колебаний (I - I) плоскополяризованного света, падающего на него. Введение кварцевой пластины приводит к повороту плоскости колебаний света на угол

(1)

где l - толщина пластины.

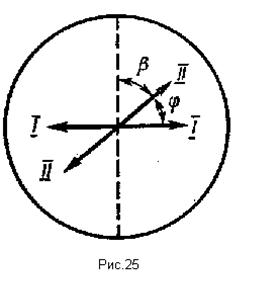Зная, во сколько раз уменьшится интенсивность света при прохождении его через поляроид, определим угол b, который установится между плоскостью пропускания поляроида и новым направлением (II - II) плоскости колебаний падающего на поляроид плоскополяризованного света. Для этого воспользуемся законом Малюса

Заметив, что можно написать

(2)

Из равенства (2) с учетом (1) получим откуда искомая толщина пластины

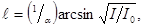
Произведем вычисления во внесистемных единицах:

Пример 7. Определить импульс ри кинетическую энергию Тэлектрона, движущегося со скоростью v = 0,9 с, где с- скорость света в вакууме.

Р е ш е н и е. Импульсом частицы называется произ­ведение массы частицы на ее скорость:

p = mv(1)

Так как скорость электрона близка к скорости света, то необходимо учесть зависимость массы от скорости, определяемую по формуле

(2)

где m - масса движущейся частицы; m₀ - масса покоя­щейся частицы; b=v/c - скорость частицы, выраженная в долях скорости света.

Заменив в формуле (1) массу mее выражением (2) и приняв во внимание, что v = cb, получим выражение для релятивистского импульса:

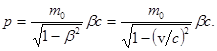(3)

Произведем вычисления:

В релятивистской механике кинетическая энергия Тчастицы определяется как разность между полной энер­гией Еи энергией покоя Е₀этой частицы, т. е. Т = Е - Е₀.

Так как E = mc²и E₀ = m₀c², то, учитывая зависимость массы от скорости, получаем 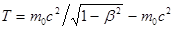или

(4)

Произведем вычисления:

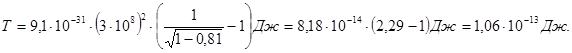
Так как во внесистемных единицах m₀c² = 0,51 МэВ, то вычисления упрощаются: T = 0,51·1,29 МэВ = 0,66 МэВ.

Пример 8. Определить релятивистский импульс элект­рона, обладающего кинетической энергией T = 5МэВ.

Р е ш е н и е. Решение задачи сводится к установле­нию соотношения между релятивистским импульсом рчастицы и ее кинетической энергией Т.

Сначала установим связь между релятивистским импульсом и полной энергией частицы. Полная энергия Ечастицы прямо пропорциональна ее массе, т. е.

Е = mс². (1)

Зависимость массы от скорости определяется фор­мулой

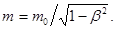(2)

Заменив массу mв формуле (1) ее выражением (2); и приняв во внимание, что m₀c² = Е₀, получим

(3)

Возведя обе части равенства (3) в квадрат, найдем откуда

(4)

Очевидно, что

Поэтому равенство (4) можно переписать в виде откуда релятивистский импульс

Разность между полной энергией и энергией покоя есть кинетическая энергия Тчастицы: Е - Е₀ = Т. Легко убе­диться, что

Е + Е₀ = Т + 2Е₀, поэтому искомая связь между импульсом и кинетической энергией релятивист­ской частицы выразится формулой

Вычисления удобно провести в два приема: сначала найти числовое значение радикала во внесистемных еди­ницах, а затем перейти к вычислению в единицах СИ. Таким образом,

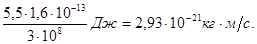
Пример 9. Длина волны, на которую приходится мак­симум энергии в спектре излучения черного тела, l = 0,58 мкм. Определить энергетическую светимость (излучательность) R_e поверхности тела.

Р е ш е и и е. Энергетическая светимость R_e абсолют­но черного тела в соответствии с законом Стефана- Больцмана пропорциональна четвертой степени термоди­намической температуры и выражается формулой (1)

где s - постоянная Стефана-Больцмана; T - термоди­намическая температура.

Температуру Тможно вычислить с помощью закона смещения Вина:

(2)

где b- постоянная закона смещения Вина.

Используя формулы (2) и (1), получаем

(3)

Произведем вычисления:

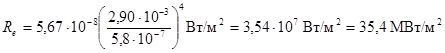
Пример 10. Определить максимальную скорость v_max фотоэлектронов, вырываемых с поверхности серебра: 1) ультрафиолетовым излучением с длиной волны l₁ = 0,155 мкм; 2) g-излучением с длиной волны l₂ =1 пм.

Р е ш е н и е. Максимальную скорость фотоэлектронов можно определить из уравнения Эйнштейна для фото­эффекта:

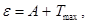(1)

где e - энергия фотонов, падающих на поверхность металла; А- работа выхода; T_max - максимальная кине­тическая энергия фотоэлектронов.

Энергия фотона вычисляется также по формуле

(2)

где h - постоянная Планка; с - скорость света в ва­кууме; l - длина волны.

Кинетическая энергия электрона может быть выра­жена или по классической формуле

(3)

или по релятивистской формуле

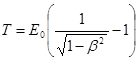(4)

в зависимости от того, какая скорость сообщается фото­электрону. Скорость фотоэлектрона зависит от энергии фотона, вызывающего фотоэффект: если энергия e фото­на много меньше энергии покоя Е₀ электрона, то может быть применена формула (3), если же e сравнима по величине с E₀, то вычисление по формуле (3) приводит к ошибке, поэтому нужно пользоваться формулой (4).

1. Вычислим энергию фотона ультрафиолетового излучения по формуле (2):

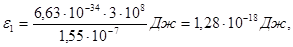
или

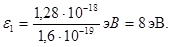
Полученная энергия фотона (8 эВ) много меньше энергии покоя электрона (0,51 МэВ). Следовательно, для данного случая кинетическая энергия фотоэлектрона в формуле (1) может быть выражена по классической формуле (3):

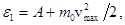
откуда

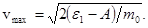(5)

Проверим, дает ли полученная формула единицу скорости. Для этого в правую часть формулы (5) вместо символов величин подставим обозначения единиц:

Найденная единица является единицей скорости.

Подставив значения величин в формулу (5), найдем

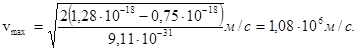
2. Вычислим энергию фотона g-излучения:

или во внесистемных единицах

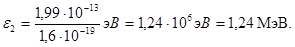
Работа выхода электрона (А = 4,7 эВ) пренебрежимо мала по сравнению с энергией фотона (e₂ = 1,24 МэВ), поэтому можно принять, что максимальная кинетическая энергия электрона равна энергии фотона: T_max = e₂ = 1,24 МэВ. Так как в данном случае кинетическая энер­гия электрона больше его энергии покоя, то для вычис­ления скорости электрона следует взять релятивистскую формулу кинетической энергии (4). Из этой формулы найдем

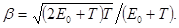
Заметив, что v = cb и T_max = e₂, получим

Произведем вычисления:

Пример 11. В результате эффекта Комптона фотон при соударении с электроном был рассеян на угол j = 90°. Энергия рассеянного фотона e₂=0,4 МэВ. Опре­делить энергию фотона e₁ до рассеяния.

Р е ш е н и е. Для определения энергии первичного фотона воспользуемся формулой Комптона:

(1)

где Dl = l₁ - l₂ - изменение длины волны фотона в ре­зультате рассеяния на свободном электроне; h - пос­тоянная Планка; m₀ - масса покоя электрона; c- ско­рость света в вакууме; j - угол рассеяния фотона.

Преобразуем формулу (1): 1) заменим в ней Dl, на l₁ - l₂; 2) выразим длины волн l₁ и l₂ и через энергии e₁ и e₂ соответствующих фотонов, воспользовавшись фор­мулой e =hc/l; 3) умножим числитель и знаменатель правой части формулы на c. Тогда

Сократим на hc и выразим из этой формулы искомую энергию:

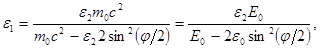(2)

где E₀ = m₀c²- энергия покоя электрона.

Вычисления по формуле (2) удобнее вести во внесистемных единицах. Так как для электрона E₀ = 0,511 МэВ, то

Пример 12. Пучок монохроматического света с длиной волны l = 663 нм падает нормально на зеркальную плоскую поверхность. Поток излучения Ф_е = 0,6 Вт. Определить: 1) силу давления F, испытываемую этой по­верхностью; 2) число фотонов ежесекундно падающих на поверхность.

Р е ш е н и е. 1. Сила светового давления на поверх­ность равна произведению светового давления p на пло­щадь S поверхности::

F =pS. (1)

Световое давление может быть найдено по формуле

p = E_e (r + 1)/c, (2)

где E_е - энергетическая освещенность;

c- скорость света в вакууме; r - коэффициент отраже­ния.

Подставляя правую часть выражения (2) в формулу (1), получаем

F = E_eS(r + 1)/c. (3)

Так как E_eS представляет собой поток излучения Ф_е, то

F = Ф_e(r + 1)/c (4)

Произведем вычисления, учитывая, что для зеркаль­ной поверхности r=1:

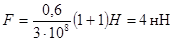
2. Произведение энергии e одного фотона на число фотонов n₁ ежесекундно падающих на поверхность, равно мощности излучения, т.е. потоку излучения: Ф_e = en₁, а так как энергия фотона e = hc/l,то

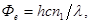
откуда

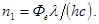(5)

Произведем вычисления:

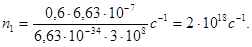
Дата добавления: 2014-11-16