Примеры решения задач. Пример 1. Электрон в атоме водорода перешел с чет­вертого энергетического уровня на второй

Пример 1. Электрон в атоме водорода перешел с чет­вертого энергетического уровня на второй. Определить энергию испущенного при этом фотона.

Р е ш е н и е. Для определения энергии фотона вос­пользуемся сериальной формулой для водородоподобных ионов:

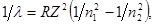(1)

где l - длина волны фотона; R - постоянная Ридберга; Z - заряд ядра в относительных единицах (при Z = 1формула переходит в сериальную формулу для водо­рода); n₁ - номер орбиты, на которую перешел электрон; n₂ - номер орбиты, с которой перешел электрон (n₁ и n₂ - главные квантовые числа).

Энергия фотона e выражается формулой

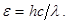
Поэтому, умножив обе части равенства (1) на hс, получим выражение для энергии фотона:

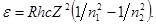
Так как Rhc есть энергия ионизации E_iатома водорода, то

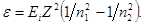
Вычисления выполним во внесистемных единицах: E_i = 13,6 эВ (см. табл. 1 Приложения); Z=1; n₁=2; n₂=4:

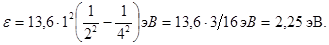
Пример 2. Электрон, начальной скоростью которого можно пренебречь, прошел ускоряющую разность потен­циалов U. Найти длину волны де Бройля электрона для двух случаев: 1) U₁ = 51 В; 2) U₂ =510 кВ.

Р е ш е н и е. Длина волны де Бройля для частицы зависит от ее импульса pи определяется формулой

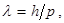(1)

где h - постоянная Планка.

Импульс частицы можно определить, если известна ее кинетическая энергия T. Связь импульса с кинетической энергией различна для нерелятивистского случая (когда кинетическая энергия частицы много меньше ее энергии покоя) и для релятивистского случая (когда кинетиче­ская энергия сравнима с энергией покоя частицы).

В нерелятивистском случае

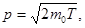(2)

где m₀ - масса покоя частицы.

В релятивистском случае

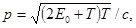(3)

где E₀ = m₀c² - энергия покоя частицы.

Формула (1) с учетом соотношений (2) и (3) запи­шется:

в нерелятивистском случае

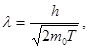(4)

в релятивистском случае

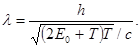(5)

Сравним кинетические энергии электрона, прошедше­го заданные в условии задачи разности потенциалов U₁=51 В и U₂=510кВ, с энергией покоя электрона и в зависимости от этого решим, какую из формул (4) или (5) следует применить для вычисления длины волны де Бройля.

Как известно, кинетическая энергия электрона прошедшего ускоряющую разность потенциалов U,

В первом случае T₁ = eU = 51эВ = 0,51×10^-4МэВ, что много меньше энергия покоя электрона Е₀ = m₀c² = 0,51МэВ. Следовательно, в этом случае можно приме­нить формулу (4). Для упрощения расчетов заметим, что Т₁ = 10^-4m₀c². Подставив это выражение в форму­лу (4), перепишем ее в виде

Учитывая, что h/m₀c есть комптоновская длина вол­ны L, получаем

Так как L = 2,43 пм (см. табл. 1 Приложения), то

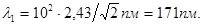
Во втором случае кинетическая энергия

T₂ = eU₂ = 510 кэВ = 0,51 МэВ, т.е. равна энергии покоя электрона. В этом случае необходимо применить релятивистскую формулу (5). Учитывая, что T₂ = 0,51 МэВ= m₀c²,по формуле (5) находим

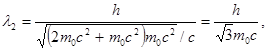
или

Подставим значение L и произведем вычисления:

Пример 3. Кинетическая энергия электрона в атоме водорода составляет величину порядка T = 10 эВ. Ис­пользуя соотношение неопределенностей, оценить мини­мальные линейные размеры атома.

Р е ш е н и е. Соотношение неопределенностей для координаты и импульса имеет вид

(1)

где Dx - неопределенность координаты частицы (в дан­ном случае электрона); Dp_x - неопределенность импуль­са частицы (электрона); 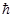- постоянная Планка.

Из соотношения неопределенностей следует, что чем точнее определяется положение частицы в пространстве, тем более неопределенным становится импульс, а следовательно, и энергия частицы. Пусть атом имеет линей­ные размеры l, тогда электрон атома будет находиться где-то в пределах области с неопределенностью

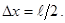
Соотношение неопределенностей (1) можно записать в этом случае в виде

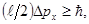
откуда

(2)

Физически разумная неопределенность импульса Dp_x во всяком случае не должна превышать значения самого импульса p_x,т.е. Dp_x£p_x. Импульс p_x связан кинети­ческой энергией Т соотношением 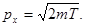Заменим Dp_xзначением (такая замена не увеличит l). Переходя от неравенства к равенству, получим

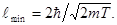(3)

Проверим, дает ли полученная формула единицу длины. Для этого в правую часть формулы (3) вместо симво­лов величин подставим обозначения их единиц:

Найденная единица является единицей длины.

Произведем вычисления:

Пример 4. Вычислить дефект массы и энергию связи ядра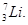

Р е ш е н и е. Масса ядра всегда меньше суммы масс свободных (находящихся вне ядра) протонов и нейтро­нов, из которых ядро образовалось. Дефект массы ядра Dm и есть разность между суммой масс свободных нукло­нов (протонов и нейтронов) и массой ядра, т.е.

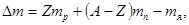(1)

где Z - атомный номер (число протонов в ядре); A - массовое число (число нуклонов, составляющих ядро); m_р, m_n, m_я- соответственно массы протона, нейтрона и ядра.

В справочных таблицах всегда даются массы нейт­ральных атомов, но не ядер, поэтому формулу (1) целе­сообразно преобразовать так, чтобы в нее входила мас­са m_а нейтрального атома. Можно считать, что масса нейтрального атома равна сумме масс ядра и электронов, составляющих электронную оболочку атома: m_a = m_я + Zm_e, откуда

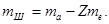(2)

Выразив в равенстве (1) массу ядра по формуле (2), получаем

Dm =Zm_p + (A - Z)m_n - m_a +Zm_e, или

Замечая, что m_p + m_e = m_H, где m_H - масса атома водорода, окончательно находим

(3)

Подставив в выражение (3) числовые значения масс (см. табл. 13 и 15 Приложения), получим

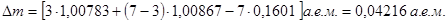
В соответствии с законом пропорциональности массы и энергии

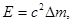(4)

где с - скорость света в вакууме.

Коэффициент пропорциональности с² может быть вы­ражен двояко:

с² = 9·10¹⁶ м²/с², или с² = DE/Dm = 9·10¹⁶ Дж/кг.

Если вычислить энергию связи, пользуясь внесистемными единицами, то с² = 931МэВ/а.е.м. С учетом этого формула (4) примет вид

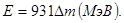(5)

Подставив найденное значение дефекта массы ядра в формулу (5), получим

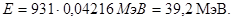
Примечание. Термин «дефект массы» часто применяют в другом смысле: дефектом массы D называют разность между массой нейтрального атома данного изотопа и его массовым числом A:

D = m_a - A. Эта величина особого физического смысла не имеет, но ее использование позволяет в ряде случаев значительно упростить вычисления. В на­стоящем пособии всюду имеется в виду дефект массы Dm, определяемый формулой (1).

Пример 5. При соударении a - частицы с ядром бора 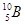произошла ядерная реакция, в результате которой образовалось два новых ядра. Одним из этих ядер было ядро атома водорода 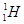. Определить порядковый номер и массовое число второго ядра, дать символическую запись ядерной реакций и определить ее энергетический эффект.

Р е ш е н и е. Обозначим неизвестное ядро символом . Так как a-частица представляет собой ядро гелия 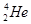, запись реакции имеет вид

Применив закон сохранения числа нуклонов, полу­чим уравнение

4 + 10 = 1 + A, откуда A = 13. Применив закон сохранения заряда, получим уравнение 2 + 5 = 1 + Z, откуда Z = 6. Следовательно, неизвестное ядро является ядром атома изотопа углерода

Теперь можем записать реакцию в окончательном виде:

Энергетический эффект Qядерной реакции определя­ется по формуле

Здесь в первых круглых скобках указаны массы исходных ядер, во вторых скобках - массы ядер - про­дуктов реакции. При числовых подсчетах по этой форму­ле массы ядер заменяют массами нейтральных атомов. Возможность такой замены вытекает из следующих соображений.

Число электронов в электронной оболочке нейтраль­ного атома равно его зарядовому числу Z. Сумма заря­довых чисел исходных ядер равна сумме зарядовых чисел ядер - продуктов реакции. Следовательно, электронные оболочки ядер гелия и бора содержат вместе столько же электронов, сколько их содержат электронные оболочки ядер углерода и водорода.

Очевидно, что при вычитании суммы масс нейтраль­ных атомов углерода и водорода из суммы масс атомов гелия и бора массы электронов выпадут и мы получим тот же результат, как если бы брали массы ядер. Подста­вив массы атомов (см. Табл. 13 Приложения) в расчет­ную формулу, получим

Пример 6. Определить начальную активность A₀ радиоактивного препарата магния 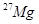массой m = 0,2 мкг, а также его активность Aчерез время t = 6ч. Период полураспада T_1/2 магния считать известным.

Р е ш е н и е. Активность Aизотопа характеризует скорость радиоактивного распада и определяется отно­шением числа dN ядер, распавшихся за интервал вре­мени dt, к этому интервалу:

(1)

Знак «-» показывает, что число N радиоактивных ядер с течением времени убывает.

Для того чтобы найти dN/dt,воспользуемся законом радиоактивного распада:

(2)

где N - число радиоактивных ядер, содержащихся в изотопе, в момент времени t; N₀ - число радиоактивных ядер в момент времени, принятый за начальный (t = 0); l - постоянная радиоактивного распада.

Продифференцируем выражение (2) по времени:

(3)

Исключив из формул (1) и (3) dN/dt, находим актив­ность препарата в момент времени t:

(4)

Начальную активность A₀препарата получим при t=0:

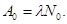(5)

Постоянная радиоактивного распада l связана с пе­риодом полураспада T_1/2 соотношением

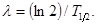(6)

Число N₀ радиоактивных ядер, содержащихся в изо­топе, равно произведению постоянной Авогадро N_A на количество вещества n данного изотопа:

(7)

где m- масса изотопа; M- молярная масса.

С учетом выражений (6) и (7) формулы (5) и (4) принимают вид

(8)

(9)

Произведем вычисления, учитывая, что T_1/2 = 10 мин = 600 с (см. табл. 14 Приложения), 1n2 = 0,693, t = 6ч = 6×3,6×10³с = 2,16. 10⁴с:

Пример 7. Вычислить максимальную энергию e_F (энергию Ферми), которую могут иметь свободные элект­роны в металле (медь) при температуре T=0 К. При­нять, что на каждый атом меди приходится по одному валентному электрону.

Р е ш е н и е. Максимальная энергия e_F, которую могут иметь электроны в металле при T=0К, связана с концентрацией свободных электронов соотношением

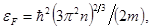(1)

где - постоянная Планка; m - масса электрона.

Концентрация свободных электронов по условию за­дачи равна концентрации атомов, которая может быть найдена по формуле

(2)

где r - плотность меди; N_A - постоянная Авогадро; M- молярная масса.

Подставляя выражение nв формулу (1), получаем

Произведем вычисления:

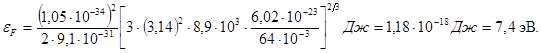
Пример 8. Кремниевый образец нагревают от тем­пературы t₁=0°С до температуры t₂=10°С. Во сколько раз возрастает его удельная проводимость?

Р е ш е н и е. Удельная проводимость g собственных полупроводников связана с температурой Tсоотноше­нием

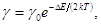
где g₀ - константа; DE- ширина запрещенной зоны.

Следовательно,

'

Полагая для кремния DE= 1,1 эВ, произведем вычис­ления:

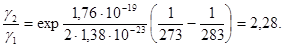
Дата добавления: 2014-11-16