Механических систем

Дифференциальные уравнения движения твердых тел и

6.1 Дифференциальные уравнения поступательного движения твердого

тела

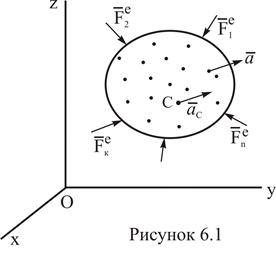Рассмотрим твердое тело совершающее поступательное движение. Твердое тело можно представить как механическую систему, на каждую точку которой действуют внешние силы .

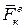Из теоремы о движении центра масс системы получаются дифференциальные уравнения поступательного движения твердого тела. Имеем:

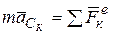
Но при поступательном движении твердого тела ускорения всех точек тела одинаковы по модулю и направлению, т.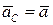е. , где 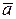- ускорение произвольной точки тела. Учитывая это, из теоремы о движении центра масс получаем следующие дифференциальное уравнение поступательного движения тела в векторной форме:

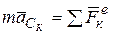(6.1)

проецируя на оси координат, имеем:

. (6.2)

Выражения (6.2) представляют собой дифференциальные уравнения поступательного движения твердого тела в проекциях на прямоугольные оси координат. В этих уравнениях х,у,z являются координатами произвольной точки тела, в частности, могут быть координатами его центра масс.

Тело, совершающее поступательное движение, имеет три степени свободы, и поэтому можно составить три дифференциальных уравнения его движения. Дифференциальные уравнения поступательного движения твердого тела аналогичны дифференциальным уравнениям движения одной материальной точки. С помощью этих уравнений можно решать такие же задачи, как и для одной его точки.

6.2 Дифференциальное уравнение вращения твердого тела вокруг

неподвижной оси

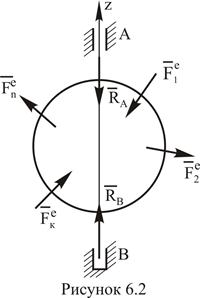Из теоремы об изменении кинетического момента (5.11) получим дифференциальное уравнение вращения твердого тела вокруг неподвижной оси Оz (рисунок 6.2) имеем

.

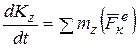Для случая вращения твердого тела вокруг неподвижной оси, согласно (5.8)

,

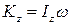где I_z – постоянный для твердого тела момент инерции относительно неподвижной оси вращения; ω – угловая скорость. Учитывая это, получаем

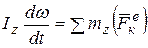(6.4)

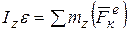или (6.5)

Если ввести угол поворота тела φ, то дифференциальные уравнения вращения тела вокруг неподвижной оси можно записать в виде:

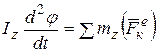(6.6)

или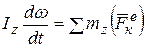

или .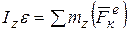

Эти уравнения аналогичны дифференциальному уравнению поступательного движения тела в проекции на какую-либо ось, например, на ось z.

В дифференциальное уравнение вращения тела вокруг неподвижной оси вместо координаты z входит угол поворота φ, вместо массы m – момент инерции относительно оси вращения. I_z, вместо суммы проекций внешних сил на ось Оz – сумма моментов внешних сил относительно оси вращения Оz.

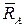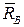Реакции подшипников и оси вращения являются внешними силами, но их моменты относительно оси вращения равны нулю, т.к. они параллельны оси (или ее пересекают). В частном случае, 1) если 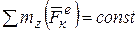, то 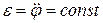т.е. вращение тела происходит с постоянным угловым ускорением; 2) если 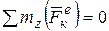, то 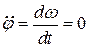; 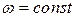, - это случай равномерного вращения тела по инерции без действия вращательного момента внешних сил.

Дифференциальное уравнение вращательного движения твердого тела в общем случае позволяет решать две основные задачи: 1) по заданному вращению тела определить вращающий момент внешних сил; и 2) по заданному вращательному моменту внешних сил и начальным условиям находить вращение тела.

6.3 Дифференциальные уравнения плоского движения твердого тела

Используя теоремы о движении центра масс и изменении кинетического момента системы относительно центра масс для относительного движения системы по отношению к системе координат, движущейся поступательно с центром масс, получим дифференциальные уравнения плоского движения твердого тела.

В плоскости движения центра масс тела, совершающего плоское движение, выберем неподвижную систему координат Ох₁у₁, относительно которой рассматривается движение, и движущуюся поступательно вместе с центром масс систему Сху (рисунок 6.3). Пусть х_С и у_С – координаты центра масс тела относительно неподвижной системы координат.

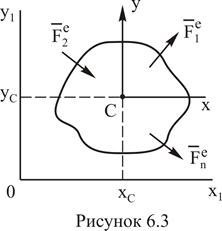Тогда по теореме о движении центра масс получим два следующих дифференциальных уравнения плоского движения твердого тела:

,

Z

где m – масса тела.

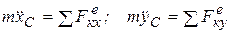Третье дифференциальное уравнение плоского движения твердого тела получим из теоремы об изменении кинетического момента в относительном движении по отношению к центру масс в проекции на подвижную ось Сz:

.

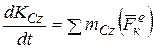Плоское движение твердого тела можно считать состоящим из поступательного движения вместе с центром масс С и вращения вокруг подвижной оси Сz. Для случая вращения вокруг оси кинетический момент относительно этой оси вычисляется по формуле:

,

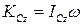где ω – угловая скорость тела;

I_Cz – момент инерции тела относительно оси Сz.

Так как I_Cz является величиной постоянной, то после подстановки К_Cz в теорему об изменении кинетического момента в относительном движении получим:

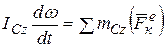или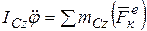

где φ – угол поворота вокруг подвижной оси Сz.

Таким образом, для твердого тела, совершающего плоское движение и, следовательно, имеющего три степени свободы, получим три следующих дифференциальных уравнения:

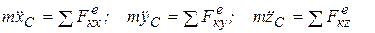(6.7)

С помощью этих уравнений можно решать две основные задачи: 1) по заданному плоскому движению твердого тела находить действующие на тело внешние силы и 2) по заданным внешним силам и начальным условиям определять его движение. При решении этих задач должны быть заданы масса тела m и его момент инерции.

Вопросы для самоконтроля

1. Записать дифференциальное уравнение движения центра масс механической системы.

2. При каких условиях центр масс механической системы находится в покое, и при каких условиях он движется равномерно и прямолинейно?

3. Записать дифференциальное уравнение вращения твердого тела вокруг неподвижной оси.

4. При каких условиях происходит равномерное вращение тела вокруг неподвижной оси, и при каких условиях тело вращается с постоянным ускорением?

5. Сколько дифференциальных уравнений движения необходимо составить, чтобы описать плоское движение тела на плоскости и в пространстве?

6. Какие действия необходимо совершить, чтобы составить дифференциальное уравнение движения механической системы, состоящей из тел?

Дата добавления: 2014-11-08