
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Кинетической энергии
|
|
|
|
Работа. Мощность. Кинетическая энергия. Теорема об изменении
7.1 Две меры механического движения
В динамике рассматриваются два случая преобразования механического движения материальной точки или системы точек:
1) механическое движение переносится с одной механической системы на другую в качестве механического движения;
2) механическое движение превращается в другую форму движения материи (в форму потенциальной энергии, теплоты, электричества и т.д.).
Каждый их этих случаев преобразования механического движения имеет свои измерители, как механического движения, так и действия силы. Когда рассматривается преобразование механического движения без перехода его в другую форму движения, мерой механического движения является вектор количества движения материальной точки  и механической системы
и механической системы  .
.
Мерой действия силы в этом случае является вектор импульса силы  . Когда механическое движение превращается в другую форму движения материи, в качестве меры механического движения выступает кинетическая энергия материальной точки или механической системы.
. Когда механическое движение превращается в другую форму движения материи, в качестве меры механического движения выступает кинетическая энергия материальной точки или механической системы.
Из элементарного курса физики известно, что кинетическая энергия материальной точки массой т, движущейся со скоростью v, равна половине произведения массы этой точки на квадрат скорости ее движения.
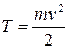 (7.1)
(7.1)
Мерой действия силы при превращении механического движения в другую форму движения является работа силы. Итак, существуют две различные меры механического движения:  и
и  - и две различные меры действия силы: импульс силы
- и две различные меры действия силы: импульс силы  и работа силы А. Следует отметить, что в первом случае это векторные величины (
и работа силы А. Следует отметить, что в первом случае это векторные величины (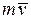 и
и  ), а во втором – скалярные (
), а во втором – скалярные ( и А). Вопрос о выборе меры механического движения был предметом многолетней полемики между сторонниками Декарта (1596-1650 г.) и сторонниками Лейбница (1646-1716 г.). Декарт считал, что мерой механического движения является количество движения
и А). Вопрос о выборе меры механического движения был предметом многолетней полемики между сторонниками Декарта (1596-1650 г.) и сторонниками Лейбница (1646-1716 г.). Декарт считал, что мерой механического движения является количество движения 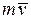 , а Лейбниц утверждал, что динамические свойства тел характеризуются величиной
, а Лейбниц утверждал, что динамические свойства тел характеризуются величиной  . Этот спор был разрешен Ф. Энгельсом, который в своей работе «Диалектика природы» показал существование двух мер механического движения, но энергия (или работа) является более общей и универсальной мерой.
. Этот спор был разрешен Ф. Энгельсом, который в своей работе «Диалектика природы» показал существование двух мер механического движения, но энергия (или работа) является более общей и универсальной мерой.
7.2 Кинетическая энергия механической системы
Для свободной механической системы, теоретическую модель которой можно представить как совокупность п точек кинетическая энергия
 , (7.2)
, (7.2)
где  - кинетическая энергия к-й точки.
- кинетическая энергия к-й точки.
Так как скалярный квадрат любого вектора равен квадрату модуля этого вектора, то Т всегда больше нуля, т.е. кинетическая энергия как материальной точки, так и механической системы не зависит от направления скоростей точек.
Кинетическая энергия может быть равна нулю для механической системы только при условии, что все точки системы находятся в покое.
Кинетическая энергия может быть использована как характеристика и поступательного, и вращательного движений.
Главное отличие величины Т от введенных ранее характеристик  и
и 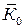 состоит в том, что кинетическая энергия является скалярной величиной, притом положительной, поэтому она не зависит от направления движения частей системы и не характеризует изменение этих направлений. Величина Т отличается от
состоит в том, что кинетическая энергия является скалярной величиной, притом положительной, поэтому она не зависит от направления движения частей системы и не характеризует изменение этих направлений. Величина Т отличается от  и
и 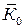 еще и тем, что на ее изменение влияет действие и внешних, и внутренних сил.
еще и тем, что на ее изменение влияет действие и внешних, и внутренних сил.
 7.2.1 Теорема Кенига
7.2.1 Теорема Кенига
Рассмотрим механическую систему, состоящую из п материальных точек, которая выполняет сложное движение (рисунок 7.1). Скорость к-й точки системы 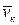 можно вычислить относительно подвижных (С ХСУСZC) и неподвижных (О Х1У1Z1) координат. Разложим движение системы на переносное поступательное движение вместе с центром масс (т.С) и относительное по отношению к системе координат, движущейся поступательно вместе в центром масс. Тогда для каждой к-й точки системы можно записать:
можно вычислить относительно подвижных (С ХСУСZC) и неподвижных (О Х1У1Z1) координат. Разложим движение системы на переносное поступательное движение вместе с центром масс (т.С) и относительное по отношению к системе координат, движущейся поступательно вместе в центром масс. Тогда для каждой к-й точки системы можно записать:
 ,
,
тогда кинетическая энергия системы будет:

где  - масса системы.
- масса системы.
Так как  , тогда
, тогда 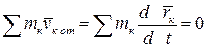 .
.
Отсюда получаем:
 . (7.3)
. (7.3)
Следовательно, кинетическая энергия механической системы в абсолютном движении складывается из кинетической энергии центра масс системы, если в нем сосредоточена вся масса системы, и кинетической энергии системы относительно центра масс – в этом заключается теорема Кенига (7.3).
7.3 Кинетическая энергия твердого тела
7.3.1 Поступательное движение твердого тела
 При поступательном движении твердого тела скорости всех его точек в каждый момент времени геометрически равны между собой. Поэтому кинетическая энергия тела определится как сумма значений кинетической энергии всех точек тела.
При поступательном движении твердого тела скорости всех его точек в каждый момент времени геометрически равны между собой. Поэтому кинетическая энергия тела определится как сумма значений кинетической энергии всех точек тела.
|
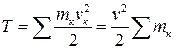 ,
,
так как  - масса тела, то окончательно:
- масса тела, то окончательно:
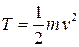 , (7.4)
, (7.4)
то есть, кинетическая энергия твердого тела, движущегося поступательно, равна половине произведения массы тела на квадрат его скорости.
Таким образом, кинетическая энергия тела, движущегося поступательно, вычисляется как кинетическая энергия материальной точки, имеющей массу тела.
 7.3.2 Вращение твердого тела вокруг
7.3.2 Вращение твердого тела вокруг
неподвижной оси
При вращении твердого тела вокруг неподвижной оси (рисунок 7.3) скорость любой точки тела  можно выразить как
можно выразить как  .
.
Кинетическую энергию твердого тела определяем по формуле (7.2):
 ,
,
где  - момент инерции тела относительно оси вращения Z.
- момент инерции тела относительно оси вращения Z.
Таким образом, кинетическая энергия тела, вращающегося вокруг неподвижной оси
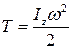 . (7.5)
. (7.5)
На основании (7.5) устанавливаем, что кинетическая энергия твердого тела, вращающегося вокруг неподвижной оси, равна половине произведения его момента инерции относительно оси вращения на квадрат угловой скорости тела.
Сравнив формулы (7.4) и (7.5), можно заметить, что при вращении тела его момент инерции играет такую же роль, как его масса при поступательном движении тела.

7.3.3 Плоское движение твердого тела
Предположим, что при плоском движении твердого тела его центр масс С движется в плоскости чертежа (рисунок 7.4). Разложим это движение на поступательное вместе с центром масс и относительное движение по отношению к центру масс.
В этом случае относительное движение представляет собой вращение тела вокруг оси ZC, проходящей через центр масс С перпендикулярно плоскости чертежа. Определим кинетическую энергию тела по теореме Кенига (7.3):
 (7.6)
(7.6)
Таким образом, при плоском движении тела его кинетическая энергия складывается из кинетической энергии поступательного движения тела вместе с центром масс и кинетической энергии вращения тела вокруг оси, проходящей через центр масс и перпендикулярной плоскости движения.
Как известно, при плоском движении тела в каждый момент времени существует точка, скорость которой равна нулю – это мгновенный центр скоростей (т.Р), следовательно, в каждый момент времени плоское движение тела можно представить как вращательное движение всех его точек вокруг м.ц.с, тогда кинетическую энергию тела можно представить
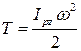 , (7.7)
, (7.7)
где 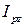 - момент инерции тела относительно оси РZ, которая проходит через т. Р –м.ц.с параллельно оси, проходящей через центр масс – т.С. Тогда по теореме Гюйгенса
- момент инерции тела относительно оси РZ, которая проходит через т. Р –м.ц.с параллельно оси, проходящей через центр масс – т.С. Тогда по теореме Гюйгенса
 ,
,
где т – масса тела.
Пример вычисления. Кинетическая энергия механической системы,
состоящей из твердых тел
Если механическая система состоит из нескольких твердых тел, то следует вычислить кинетическую энергию каждого тела, а затем полученные кинетические энергии сложить.
Eсли задать угловую скорость вращения тела ω2, то: кинетическая энергия системы будет:

Т = Т 1 + Т 2 + Т 3,
где Т 1 - кинетическая энергия поступательного движущегося тела 1;  ;
;  .
.
 - кинетическая энергия вращения тела 2 вокруг оси О, перпендикулярной плоскости рисунка.
- кинетическая энергия вращения тела 2 вокруг оси О, перпендикулярной плоскости рисунка.
Т 3 - кинетическая энергия плоского движения тела 3.
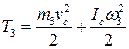 ,
,
где  .
.
Тогда кинетическая энергия механической системы будет равна
 .
.
7.4 Работа силы. Мощность силы
Для характеристики действия, оказываемого силой на тело при некотором его перемещении, вводится понятие о работе силы, широко используемое не только в механике.
7.4.1 Элементарная работа силы 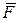
Элементарная работа dА силы 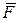 на элементарном (бесконечно малом) перемещении dS определяется следующим образом (рисунок 7.6).
на элементарном (бесконечно малом) перемещении dS определяется следующим образом (рисунок 7.6).
 (7.8)
(7.8)




|
|



|





|
|
|
|
|
|
|
|
|
|

|
|

|
|
|















 (Элементарную работу обозначают dА(а не dA) так как в общем случае она не является дифференциалом функции. Ft - проекция силы F на направление скорости точки приложения силы или на направление элементарного перемещения, которое считается направленным по скорости точки. dS – модуль элементарного перемещения точки М).
(Элементарную работу обозначают dА(а не dA) так как в общем случае она не является дифференциалом функции. Ft - проекция силы F на направление скорости точки приложения силы или на направление элементарного перемещения, которое считается направленным по скорости точки. dS – модуль элементарного перемещения точки М).
Такое определение соответствует представлению о работе как о мере того действия силы, которое приводит к изменению модуля скорости точки. Если разложить силу 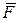 на составляющие
на составляющие  и
и  , то изменять модуль скорости будет
, то изменять модуль скорости будет  , так как
, так как  (составляющая
(составляющая  изменяет или направление вектора
изменяет или направление вектора  , или при несвободном движении – силу давления на связь).
, или при несвободном движении – силу давления на связь).
Так как  , где j - угол между
, где j - угол между 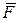 и
и  , получим из (7.4.1) другое выражение для dА:
, получим из (7.4.1) другое выражение для dА:
 (7.9)
(7.9)
Если угол j острый, то работа положительна. В частности, при j = 0, элементарная работа  . Если угол j тупой, то работа отрицательна. В частности, при j = 180 о, элементарная работа
. Если угол j тупой, то работа отрицательна. В частности, при j = 180 о, элементарная работа  . Если угол j = 90 о, т.е. если сила направлена перпендикулярно перемещению, то элементарная работа силы равна нулю.
. Если угол j = 90 о, т.е. если сила направлена перпендикулярно перемещению, то элементарная работа силы равна нулю.
Знак работы имеет следующий смысл: работа положительна, когда составляющая  направлена в сторону движения (сила ускоряет движение); работа отрицательна, когда составляющая
направлена в сторону движения (сила ускоряет движение); работа отрицательна, когда составляющая  направлена противоположно направлению движения (сила замедляет движение).
направлена противоположно направлению движения (сила замедляет движение).
Если учесть, что при бесконечно малом перемещении хорда равна дуге окружности, т.е.  , где
, где 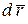 - вектор элементарного перемещения точки, то
- вектор элементарного перемещения точки, то 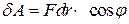
или 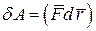 . (7.10)
. (7.10)
Следовательно, элементарная работа силы равна скалярному произведению вектора силы на вектор элементарного перемещения точки ее приложения.
Если силу 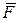 и радиус-вектор
и радиус-вектор 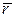 разложить по осям координат, то
разложить по осям координат, то

а  , то
, то
 . (7.11)
. (7.11)
Формулу (7.11) называют обычно аналитическим выражением элементарной работы. Если учесть, что  , то получим еще одну формулу для вычисления элементарной работы силы:
, то получим еще одну формулу для вычисления элементарной работы силы:
 , (7.12)
, (7.12)
где  - элементарный импульс силы.
- элементарный импульс силы.
Элементарная работа силы равна скалярному произведению элементарного импульса силы на скорость точки приложения силы.
Работа силы на конечном перемещении М0М1 (рисунок 7.5) вычисляется как предел интегральной суммы соответствующих элементарных работ
 (7.13)
(7.13)
или  . (7.13/)
. (7.13/)
Следовательно, работа силы на любом перемещении М0М1 равна взятому вдоль этого перемещения интегралу от элементарной работы.
Если величина  постоянна (Ft = const), то из (7.13), обозначая перемещение М0М через S 1,получим
постоянна (Ft = const), то из (7.13), обозначая перемещение М0М через S 1,получим
 . (7.14)
. (7.14)
В частности, такой случай может иметь место, когда действующая сила постоянна по модулю и направлению  , а точка, к которой приложена сила, движется прямолинейно (рисунок 7.7).
, а точка, к которой приложена сила, движется прямолинейно (рисунок 7.7).
 В этом случае
В этом случае  и
и
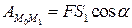 (7.14/)
(7.14/)
Единицей измерения работы в СИ является 1 Дж (1 Н·м).
7.4.2 Мощность силы
Мощностью называется величина, определяющая работу, совершаемую силой в единицу времени.
Если работа совершается равномерно, то мощность
 , (7.15)
, (7.15)
где t – время, в течение которого произведена работа А.
В общем случае
 . (7.16/)
. (7.16/)
Следовательно, мощность равна произведению касательной составляющей силы на скорость. Равенство (7.16/) с учетом (7.10) можно представить
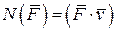 (7.16)
(7.16)
Мощность силы равна скалярному произведению силы на скорость точки приложения силы. Единицей измерения мощности в СИ является ватт (1 Вт = 1 Дж/с).
Работу, произведенную машиной, можно измерять произведением ее мощности на время работы. Отсюда возникла употребительная в технике единица измерения работы киловатт-час (1 квт час= 3,6· 106 Дж).
Из формулы (7.16/) видно, что у двигателя имеющего данную мощность N сила тяги  будет тем больше, чем меньше скорость
будет тем больше, чем меньше скорость  . Поэтому, например, на подъеме или на плохом участке дороги у автомобиля включают низкие передачи, позволяющие при полной мощности двигаться с меньшей скоростью и развивать большую силу тяги. На спуске или на хорошем участке дороги поступают обратным образом: включают высшие передачи и при полной мощности увеличивают скорость движения и уменьшают силу тяги.
. Поэтому, например, на подъеме или на плохом участке дороги у автомобиля включают низкие передачи, позволяющие при полной мощности двигаться с меньшей скоростью и развивать большую силу тяги. На спуске или на хорошем участке дороги поступают обратным образом: включают высшие передачи и при полной мощности увеличивают скорость движения и уменьшают силу тяги.
 7.4.3 Работа и мощность сил, приложенных к
7.4.3 Работа и мощность сил, приложенных к
вращающемуся телу
При вращении твердого тела вокруг неподвижной оси скорость точки М можно вычислить по векторной формуле Эйлера (рисунок 7.8): 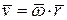 , тогда элементарную работу силы
, тогда элементарную работу силы 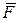 определим по формуле
определим по формуле
 ,
,
или, учитывая, что  ,
,
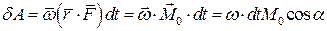 так как
так как  является моментом силы относительно точки О.
является моментом силы относительно точки О.
Учитывая, что М0 соsa = Мz – момент силы относительно оси вращения ОZ и ωdt = dj, окончательно получаем
 (7.17)
(7.17)
В частном случае, если момент силы относительно оси вращения является постоянным, т.е.  , работу определяют по формуле
, работу определяют по формуле
 , (7.18)
, (7.18)
где j 1 – угол поворота тела, на котором вычисляют работу силы.
Так как  , то мощность в случае вращения твердого тела вокруг неподвижной оси
, то мощность в случае вращения твердого тела вокруг неподвижной оси
 (7.19)
(7.19)
Мощность силы, приложенной к вращающемуся вокруг неподвижной оси твердому телу, равна произведению угловой скорости тела на момент силы относительно оси вращения тела. Знак элементарной работы и мощности в (7.18) и (7.19) зависит от того, совпадают или нет направления момента и угловой скорости: (или угла поворота) если совпадают – знак (+), не совпадают – знак (-).
7.4.4 Примеры вычисления работы
7.4.4.1 Работа силы тяжести
Пусть точка М, на которую действует сила тяжести  , перемещается из положения М0(х0, у0, z0) в положение М1(х1, у1, z1). Выберем координатные оси так, чтобы ось ОZ была направлена вертикально вверх (рисунок 7.9). Тогда Рх=0; Ру=0; Рz= –Р.
, перемещается из положения М0(х0, у0, z0) в положение М1(х1, у1, z1). Выберем координатные оси так, чтобы ось ОZ была направлена вертикально вверх (рисунок 7.9). Тогда Рх=0; Ру=0; Рz= –Р.
Подставляя эти значения в формулу (7.4.6/) получим, учитывая, что переменным интегрирования является z:
 .
.
Если точка М0 выше М1, то z 0- z 1= h, где h – вертикальное перемещение точки, если же точка М0 ниже М1, то z 0 - z 1 = - (z 1 – z 0) = - h.
Окончательно получаем
 . (7.20)
. (7.20)
 Следовательно, работа силы тяжести равна взятому со знаком плюс или минус произведению модуля силы на вертикальное перемещение точки ее приложения.
Следовательно, работа силы тяжести равна взятому со знаком плюс или минус произведению модуля силы на вертикальное перемещение точки ее приложения.
Работа положительна, если начальная точка выше конечной, и отрицательна, если начальная точка ниже конечной.
Из полученного результата следует, что работа силы тяжести не зависит от вида траектории, по которой перемещается точка ее приложения. Силы, обладающие таким свойством, называются потенциальными.
7.4.4.2 Работа силы упругости
 Рассмотрим груз М, лежащий на горизонтальной плоскости и прикрепленный к свободному концу пружины (рисунок 7.10,а).
Рассмотрим груз М, лежащий на горизонтальной плоскости и прикрепленный к свободному концу пружины (рисунок 7.10,а).
Отметим точкой О положение, занимаемое концом недеформированной пружины. Если растянуть пружину, переместив груз в положение М, то на груз будет действовать сила упругости Fупр, направленная к положению равновесия О. Тогда по закону Гука сила упругости Fупр = – сх, где с – коэффициент жесткости пружины, его размерность Н/м, х – деформация пружины. Пусть под действием силы упругости точка М переместилась из положения М0(х0) в положение М1(х1), тогда пользуясь формулой (7.13/) получим:
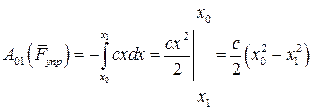 (7.21)
(7.21)
где х 0и х 1 – начальное и конечное удлинение пружины.
Этот же результат можно получить по графику зависимости  от х (рисунок 7.10,б), вычисляя площадь s заштрихованной на чертеже трапеции и учитывая знак работы. Таким образом, работа силы упругости равна половине произведения коэффициента жесткости на разность квадратов начального и конечного удлинений (сжатий) пружины.
от х (рисунок 7.10,б), вычисляя площадь s заштрихованной на чертеже трапеции и учитывая знак работы. Таким образом, работа силы упругости равна половине произведения коэффициента жесткости на разность квадратов начального и конечного удлинений (сжатий) пружины.
Работа будет положительной, когда х0>х1, т.е. когда конец пружины перемещается к равновесному положению (сжатие), и отрицательной, когда х0<х1, т.е. когда конец пружины удаляется от равновесного положения (растяжение). Таким образом, работа силы  зависит только от значений х0 и х1 и не зависит от вида траектории точки М, т.е. сила упругости также является потенциальной силой.
зависит только от значений х0 и х1 и не зависит от вида траектории точки М, т.е. сила упругости также является потенциальной силой.
7.4.4.3 Работа силы трения
 Рассмотрим точку, движущуюся по какой-нибудь шероховатой поверхности (рисунок 7.11) или кривой. Действующая на точку сила трения равна по модулю fN, где f – коэффициент трения, а N – нормальная реакция поверхности. Направлена сила трения противоположно перемещению точки. Следовательно,
Рассмотрим точку, движущуюся по какой-нибудь шероховатой поверхности (рисунок 7.11) или кривой. Действующая на точку сила трения равна по модулю fN, где f – коэффициент трения, а N – нормальная реакция поверхности. Направлена сила трения противоположно перемещению точки. Следовательно,  , тогда по формуле (7.13)
, тогда по формуле (7.13)
 . (7.18)
. (7.18)
Если численно сила трения постоянна, то  ,
,
где S – длина дуги кривой М0М1, по которой перемещается точка.
Рисунок 7.11
Таким образом, работа силы трения при скольжении всегда отрицательна. Так как эта работа зависит от длины дуги М0М1, то сила трения является силой непотенциальной.
7.5 Теорема об изменении кинетической энергии механической системы
(дифференциальная и интегральная формы)
Рассмотрим механическую систему, состоящую из n точек, на каждую из которых действуют внешние и внутренние силы 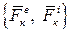 (или активные силы
(или активные силы  и реакции связей
и реакции связей  ). Рассмотрим к-ю точку системы, для нее основной закон динамики запишем в виде
). Рассмотрим к-ю точку системы, для нее основной закон динамики запишем в виде
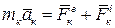
заменим  , тогда
, тогда  домножим скалярно левые и правые части данного выражения на
домножим скалярно левые и правые части данного выражения на  , тогда получим
, тогда получим
 ,
,
но  , а
, а 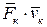 - мощность силы
- мощность силы 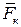 , тогда
, тогда
 , (7.19)
, (7.19)
или  (7.19/)
(7.19/)
Выражение (7.19) представляет собой теорему об изменении кинетической энергии материальной точки в дифференциальной форме: производная по времени от кинетической энергии материальной точки равна сумме мощностей внешних и внутренних сил, действующих на нее. Составляя уравнения (7.19) для каждой из точек системы и складывая их почленно, получим:
 ,
,
или  . (7.20)
. (7.20)
(7.20) представляет собой теорему об изменении кинетической энергии механической системы в дифференциальной форме.
Домножим (7.20) на dt:
 ,
,
но  - элементарная работа силы
- элементарная работа силы 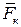 , тогда
, тогда
 . (7.20 /)
. (7.20 /)
Проинтегрируем формулу (7.20 /). Границы интегрирования в правой части определяются формулами элементарных работ (7.13) и (7.13/).
 , или
, или
 . (7.21)
. (7.21)
Выражение (7.21) представляет собой теорему об изменении кинетической энергии механической системы в интегральной форме: изменение кинетической энергии механической системы при некотором ее перемещении равно алгебраической сумме работ всех действующих на систему внешних и внутренних сил на том же перемещении. В отличие от предыдущих теорем внутренние силы в уравнениях (7.19) и (7.21) не исключатся, тогда как изменения количества движения и кинетичного момента зависят только от внешних сил
 .
.
Рассмотрим случай, когда внутренние силы не влияют на изменение кинетической энергии системы.
|
|
|
|
|
Дата добавления: 2014-11-08; Просмотров: 1141; Нарушение авторских прав?; Мы поможем в написании вашей работы!