Описание установки и методика измерений. Установка имеет основание с регулируемыми ножками, на котором расположен электронный измеритель периода крутильных колебаний и закреплена вертикальная

Установка имеет основание с регулируемыми ножками, на котором расположен электронный измеритель периода крутильных колебаний и закреплена вертикальная колонка. На колонке установлены три кронштейна, причем нижний и средний, в случае необходимости, можно перемещать вдоль колонки. На среднем кронштейне имеется площадка в виде полукольца, на которой располагаются электромагнит и фотоэлектронный датчик. При необходимости их положение можно изменять.

Колеблющаяся система состоит из двух одинаковых упругих элементов (проволок) и инерционной рамки, позволяющей закреплять дополнительные инерционные грузы (диски) с известными моментами инерции относительно продольной оси (рис.2.2).

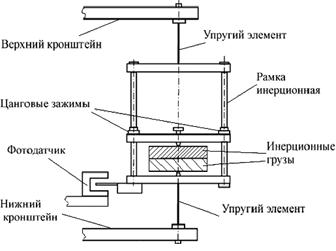
Рис.2..2

Динамическое уравнение свободных колебаний крутильного маятника имеет вид:

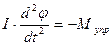, (2.13)

где I – момент инерции колеблющейся системы, 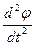– угловое ускорение, М_упр – момент упругих касательных сил. С учетом (2.11) уравнение (2.13) запишем в таком виде:

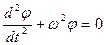, (2.14)

где 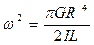. (2.15)

Заметим, что как уравнение (2.14), так и соотношение (2.15) справедливы только для упругих деформаций кручения проволочной подвески маятника.

Решая уравнение (2.14), получим:

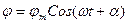. (2.16)

Здесь φ –угол поворота крутильного маятника к моменту t; φ_m – заданная угловая амплитуда колебаний. Уравнение (2.14) определяет свободные, практически гармонические, колебания вертикального крутильного маятника с периодом

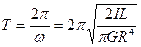. (2.17)

На самом же деле, колебания будут медленно затухающими, так как полностью силы сопротивления исключить невозможно. Из (2.17) получим формулу для модуля сдвига

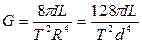, (2.18)

где d – диаметр проволочной подвески маятника. Однако, собственный момент инерции маятника неизвестен. Чтобы исключить этот параметр, необходимо иметь два дополнительных инерционных тела с известными моментами инерции, которыми нагружается маятник.

Пусть I₀ – неизвестный собственный момент инерции маятника, а I₁ и I₂ – моменты инерции дополнительных тел. В этом случае мы получим систему двух уравнений:

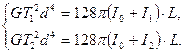(2.19)

Решая систему (2.19), получим:

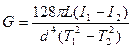, (2.20)

Здесь 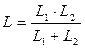, где L₁ и L₂ – длины верхней и нижней проволочных подвесок маятника.

Дата добавления: 2014-11-16