Описание установки и методика измерения

Лабораторная работа № 1.4.

МАЯТНИКА МАКСВЕЛЛА

МЕТАЛЛИЧЕСКИХ КОЛЕЦ ПРИ ПОМОЩИ

ИЗМЕРЕНИЕ МОМЕНТА ИНЕРЦИИ

Цель работы: экспериментально убедиться в справедливости закона сохранения энергии консервативной системы во время движения, а затем на основе этого закона измерить моменты инерции некоторых металлических колец при помощи маятника Максвелла.

Оборудование: маятник Максвелла, набор металличе- ских колец с известными и неизвестными моментами инерции.

Маятник Максвелла представляет собой ролик (маховичок), который закреплен на оси и бифилярным способом горизонтально подвешен на неподвижной балке. На ролик маятника могут накладываться сменные металлические кольца, позволяющие изменить момент инерции системы (рис.4.1)

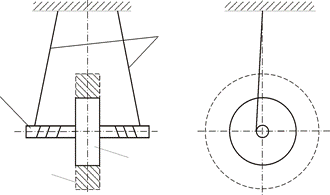
Рис.4.1

Маятник Максвелла является основной частью лабораторной установки, содержащей электромагнит, фотодатчики и электронный измеритель времени.

Если сначала поднять маятник до некоторой высоты, наматывая нити подвеса виток к витку на валик путем его поворота, а затем отпустить, то он достаточно длительное время будет совершать периодические движения вниз-вверх. Отсюда, собственно, и название системы «маятник». В момент достижения маятником нижнего положения происходит упругий удар, в результате которого скорость поступательного движения получает противоположное направление, практически не меняя своей величины. Направление же вращательного движения остается прежним. В результате этого нити подвеса будут навиваться на ось в противоположном направлении, и маятник будет подниматься вверх. Процесс перемещения маятника вниз-вверх будет многократным.

Если пренебрегать силами сопротивления, то маятник Максвелла в целом можно рассматривать как консервативную систему, а его движение – соответствующее закону сохранения механической энергии.

Пусть m – масса маятника, I – его момент инерции. Положение маятника в текущий момент времени будем определять координатой x центра масс относительно его начального положения x = 0 в момент t = 0.

На рис.4.2 указаны основные силы, действующие на тело маятника, и направления его движений. Считаем, что нити подвески маятника практически вертикальны. Заменяем действие двух нитей на тело их суммарной реакцией N. На основании законов динамики плоско-параллельного движения тела имеем два уравнения:

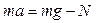, (4.1)

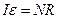. (4.2)

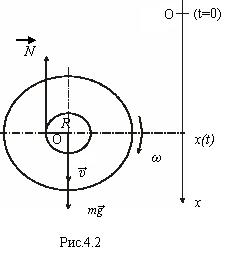
Здесь a –ускорение вертикального перемещения тела вниз, 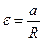- угловое ускорение вращательного движения тела вокруг центральной оси О.

Из данной системы уравнений определяем

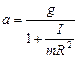, (4.3)

и координату 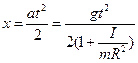. (4.4)

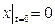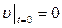При начальных условиях и , при этом скорость поступательного движения и кинетическая энергия тела к моменту времени t соответственно будут равны

, (4.5)

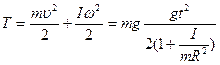. (4.6)

Для консервативной системы полная механическая энергия Е = Т + U = const. Отсюда следует, что приращение кинетической энергии системы равно убыли её потенциальной энергии, т.е. .

Применительно к маятнику 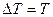(Т₁=0, Т₂=Т), -

, где h – высота на которую опустился маятник за время t.

Следовательно,

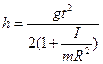. (4.7)

Высоте h задается определенное значение, которое в процессе всех опытов остается неизменным. Варьируя величиной момента инерции маятниковой системы при помощи сменных колец, будем путем измерений получать соответствующие промежутки времени t. Из равенства (4.7) для квадрата времени получим

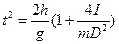, (4.8)

где D = 2 R - диаметр навивки нитей подвеса, а для момента инерции получим следующее соотношение

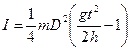. (4.9)

Отсюда следует, что выполнение данной лабораторной работы будет состоять из двух пунктов:

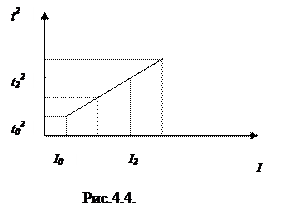
а) убедиться в справедливости соотношения (4.8), т.е. в действии закона сохранения механической энергии. При этом для заданных значений момента инерции системы измеряется время опускания как нагруженного, так и ненагруженного маятника до крайнего нижнего положения. В результате этих измерений получим последовательность точек (I_к, t²_к). Нанося эти точки на плоскость t² (I), мы увидим линейную зависимость t² от I, примерно изображенную на рис.4.4. Заметим, что погрешность полученных результатов не должна превышать 2 - 4%.

б) убедившись в непосредственном действии закона сохранения энергии, в этом пункте предстоит определить момент инерции нескольких металлических колец, накладываемых на ролик маятника. По данным измерений времени и известным значениям других величин по формуле

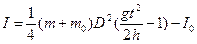
найдем момент инерции кольца.

Здесь m₀ и I₀ - собственные значения массы и момента инерции маятника соответственно, а m -масса кольца.

Дата добавления: 2014-11-16