Описание прибора и методика измерений

С ПОМОЩЬЮ БАЛЛИСТИЧЕСКОГО МАЯТНИКА

ОПРЕДЕЛЕНИЕ СКОРОСТИ ПОЛЕТА ПУЛИ

Лабораторная работа № 1.6.

Цель работы: освоение методики определения скорости полёта пули с помощью баллистического маятника.

Принадлежности: баллистический маятник, пружинная пушка, миллиметровая шкала отсчета, набор снарядов (пуль), технические весы, штангенциркуль с ценой деления 0,1 мм.

Рис. 6.1

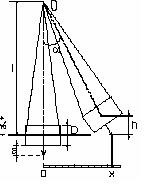Баллистический маятник представляет собой цилиндр, частично заполненный вязким веществом (воском, парафином, пластилином), подвешенный на длинных легких нитях (рис. 6.1.) В маятник стреляют из «пушки» так, чтобы полет снаряда непосредственно перед ударом происходил по оси

цилиндра. Снаряд массы m застревает в слое пластилина, и система «снаряд-маятник» как целое приобретает пределенный начальный момент импульса относительно оси О.

Система «снаряд-маятник» в общем не является замкнутой, однако в горизонтальной плоскости ее можно рассматривать в процессе удара как изолированную. Кроме того, если время соударения пули с маятником мало (по сравнению с периодом колебаний), то маятник за время удара не успевает заметно отклониться от исходного положения. Это значит, что во время удара не возникает сила, стремящаяся вернуть маятник в исходное состояние. В таком случае на систему «снаряд-маятник» во времяудараможно распространить действие закона сохранения момента импульса, и, следовательно, написать

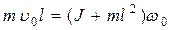, (6.1)

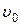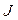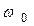где - скорость пули до удара; и - момент инерции маятника относительно оси вращения и его начальная угловая скорость;

Рис.6.1

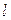- расстояние от центра тяжести маятника до оси О, приблизительно равное длине нитей подвеса.

В уравнении (6.1) левая часть дает выражение момента импульса снаряда относительно оси вращения в начале удара, правая – момента импульса маятника вместе c застрявшим в нем

Рис.1

снарядом, относительно той же оси в конце удара. Далее, применяя к движущейся системе после удара закон сохранения энергии, получим еще одно соотношение:

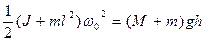, (6.2)

где 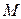- масса маятника (цилиндра); 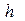- высота подъема центра тяжести маятника после удара.

Величину 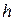можно определить из измерений отклонения маятника от положения равновесия при попадании снаряда. Из рисунка видно, что

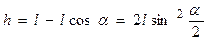, (6.3) где 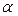- угол отклонения маятника от положения равновесия.

Подставив (6.3) в (6.2), получим

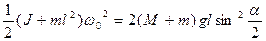. (6.4)

В этом уравнении левая часть дает выражение кинетической энергии в первый момент времени по окончании удара, правая часть дает выражение потенциальной энергии системы в момент достижения наибольшего отклонения.

Из уравнения (6.1), принимая во внимание уравнение (6.4), находим

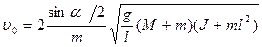. (6.5)

Так как размеры маятника малы по сравнению с длиной нити подвеса, то данный маятник можно рассматривать как математический. Полагая 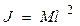, получим

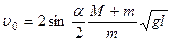. (6.6)

В свою очередь, угол 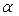можно определить из условия

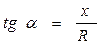, (6.7)

где 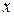- смещение стрелки от нулевого деления шкалы; 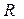- расстояние острия стрелки до точки подвеса. Из рис.6.1:

, (6.8)

где 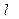- длина нити подвеса; 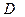- диаметр цилиндра; 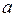- длина стрелки.

Для малых отклонений маятника можно считать

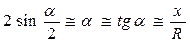. (6.9)

Подставив (6.9) в (6.6), получим окончательную формулу для скорости полета пули

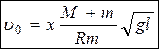. (6.10)

Дата добавления: 2014-11-16