План исследования функции и построения графика

Вопросы для самопроверки.

1. Сформулировать определение производной.

2. Каков геометрический смысл производной?

3. Как составить уравнение касательной?

4. Каков геометрический и механический смысл производной?

5. Как найти производную неявной функции? Параметрической функции?

6. Функция непрерывна в т. x_0. Следует ли отсюда дифференцируемость функции?

7. В чём заключается геометрический смысл дифференциала функции?

8. Записать формулу, используемую в приближённых вычислениях. Найти приближённое значение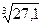

Тема 6. Приложения производной к исследованию поведения функции и построению графика и к другим задачам.

Пискунов, гл. V, §1-12, упр 1-134

Данко, ч. I, гл. 3

1.Найти область определения функции. Решение этого вопроса указывает на те интервалы оси (ОХ), над которыми пройдёт график и на те значения аргумента x, над которыми график не пройдёт, а также в каких точках пройдут вертикальные асимптоты.

2.Исследовать на чётность, нечётность. Решение этого вопроса облегчает построение.

3.Указать промежутки монотонности функции и найти экстремумы её, точки экстремумов. Построить соответствующие точки на координатной плоскости.

4.Указать точки перегиба графика функции и нанести их на координатную плоскость. Указать промежутки выпуклости, вогнутости.

5.Найти уравнения вертикальных и наклонных асимптот, используя условия для существования этих асимптот. Построить эти линии на координатной плоскости.

6.Найти точки пересечения графика функции с осями координат. Нанести их на плоскость.

7.Исследовать поведение функции на концах области определения. Это поможет при построении графика.

8.Можно взять несколько контрольных точек, в случае уточнения поведения графика.

9.Построить график.

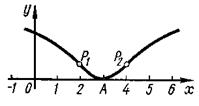
Задача 1. Исследовать функцию у = 1п(х² — 6х +10) и построить ее график.

Решение:

1. Определим область существования функции. Квадратный трехчлен, стоящий под знаком ло­гарифма, можно представить так: х²— 6x+10=(x-3)² + 1. Как видно, под знаком логарифма будет положи­тельное число при любом значении аргумента х. Следо­вательно, областью существования данной функции слу­жит вся числовая ось.

2. Исследуем функцию на непрерывность. Функция всюду непрерывна и не имеет точек разрыва.

3. Установим четность и нечетность функции. Так как у(-х)¹у(х) и у(- х)¹ - у(х), то функция не яв­ляется ни четной, ни нечетной.

4. Исследуем функцию на экстремум. Находим пер­вую производную:

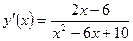
Знаменатель х²- 6x+10>0 для любого значения х. Как видно, при х < 3 первая производная отрицательна, а при х > 3 положительна. При х = 3 первая производная меняет свой знак с минуса на плюс. В этой точке функ­ция имеет минимум:

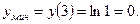
Итак, A(3; 0) - точка минимума. Функция убывает на интервале (- ¥, 3) и возрастает на интервале (3, + ¥).

5. Определим точки перегиба графика функции и интервалы выпуклости и вогнутости кривой. Для этого находим вторую производную:

Разобьем всю числовую ось на три интервала: (- ¥, 2), (2, 4), (4, + ¥). Как видно, в первом и третьем интерва­лах вторая производная отрицательна, а во втором ин­тервале положительна. При x₁ = 2 и х₂ = 4 вторая произ­водная меняет свой знак. Эти значения аргумента явля­ются абсциссами точек перегиба. Определим ординаты этих точек:

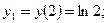
Следовательно, P₁ (2; ln 2) и P₂(4; ln 2) — точки перегиба графика функции. График является выпуклым в интерва­лах (- ¥, 2) и (4, +¥) и вогнутым в интервале (2, 4).

6. Определим уравнения асимптот графика функции. Для определения уравнения асимптоты y=kx+b вос­пользуемся формулами:

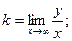
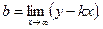
Имеем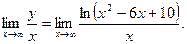

Чтобы найти искомый предел, дважды применяем правило Лопиталя:

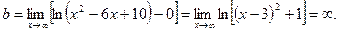
Итак, кривая не имеет асимптот.

Использование производной в задачах прикладного характера.

Задача 1. Найти такой цилиндр, который имел бы наибольший объём при данной полной поверхности S.

Решение: Пусть радиус основания цилиндра равен x, а высота равна y.

Тогда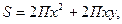

Следовательно, объём цилиндра выразится так:

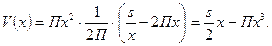
Задача сводится к исследованию функции V(x) на максимум при x > 0.

и приравняем её к нулю, откуда

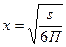
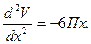
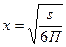
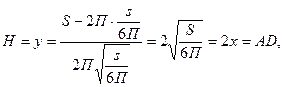
Найдём производную

Найдём

,то объём имеет,

выполняется условие

При

	наибольшее значение причем

т.е осевое сечение цилиндра должно быть квадратом.

Ответ: Цилиндр с квадратным сечением имеет наибольший объём при данной полной поверхности S.

Дата добавления: 2014-11-16