
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Операции над векторами
|
|
|
|
Тема 3. Основы векторной алгебры.
Ефимов, гл. 7,8
Клетенник, гл. 8,9; Данко, гл. 2.
1. 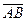 - направленный отрезок.
- направленный отрезок.
- Сложение векторов.
 |



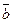

 +
+ 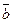
или
 |  |
 +
+ 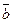
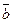
- Вычитание векторов.
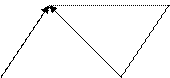 |

 -
- 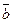

 -
- 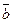 или
или 
 |
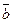
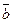
- Умножение вектора на число.

 3
3 

 Þ | | |
Þ | | |
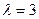
-3 

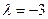 Þ | | |
Þ | | |
- Скалярное произведение.

1)  ·
· 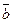 =
= 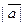


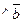 )
)
2)  ·
· 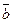 =P, P- число
=P, P- число
3)  =
= 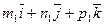
4) 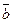 =
= 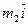

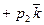
Свойства:
1).  ·
· 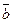 =
= 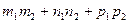 -скалярное произведение векторов, заданных координатами.
-скалярное произведение векторов, заданных координатами.
2).  cos j=
cos j= 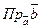 (проекция вектора
(проекция вектора 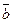 на
на  ). Поэтому
). Поэтому
 ·
· 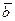 =
= 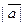
 cos j=
cos j= 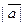
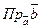 =
= 
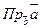
3).  =
=  ,
, 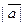 =
=  , где
, где 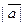 =
= 
4).  ·
· 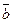 =0, если
=0, если  ^
^ 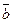
5). 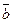 =
= 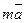 или
или  -условие коллинеарности векторов.
-условие коллинеарности векторов.
6). Угол между векторами:
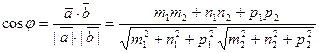 ,
,  - условие перпендикулярности двух векторов.
- условие перпендикулярности двух векторов.
7).  ·
· 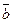 =
= 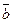 ·
· 
8).  ·
· 
9). 
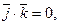

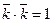
- Векторное произведение
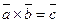
удовлетворяет условиям:

1). 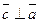 и
и 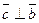
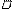 2).
2). 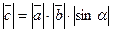

3). 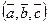 -образуют такую же ориентацию как
-образуют такую же ориентацию как 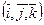
Свойства:
1).  =
= 
2). 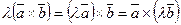 , где
, где 
3). 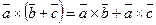
4). Если 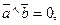 то
то 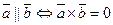
5). 
6). Если  , то
, то 
7.)  - площадь параллелограмма.
- площадь параллелограмма.
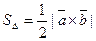 -площадь треугольника.
-площадь треугольника.
8). 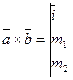

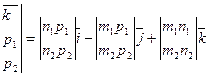
9). 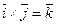
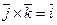

- Смешанное произведение.
1). 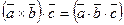 -форма записи смешанного произведения.
-форма записи смешанного произведения.
2). 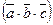 =
= 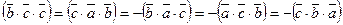
3). Если  -компланарны, то
-компланарны, то 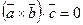
4). 

 , если
, если 
5). 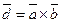
 |
Д1 С1
М A1
 В1
В1
Д С

А  В
В
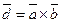
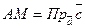
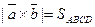


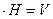 , где V-объём параллелепипеда.
, где V-объём параллелепипеда.

3. 2 Примеры решения задач.
Задача 5. Даны координаты вершин пирамиды ABCD: А (2; 1; 0), B (3; -1; 2), С (13; 3; 10), D (0; 1; 4). Требуется: 1) записать векторы  и
и 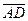 в системе орт
в системе орт 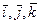 и найти модули этих векторов; 2) найти угол между векторами
и найти модули этих векторов; 2) найти угол между векторами 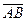 и
и  ; 3) найти проекцию вектора
; 3) найти проекцию вектора 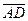 на вектор
на вектор 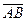 ; 4) найти площадь грани ABC; 5) найти объем пирамиды ABCD.
; 4) найти площадь грани ABC; 5) найти объем пирамиды ABCD.
Решение. I. Произвольный вектор а может быть представлен в системе орт i, j, k  следующей формулой;
следующей формулой;
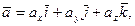 (1)
(1)
где ах, ау, аг — проекции вектора а на координатные оси Ох, Оу и Oz, а 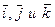 — единичные векторы, направления которых совпадают с положительным направлением осей Ох, Оу и Oz. Если даны точки
— единичные векторы, направления которых совпадают с положительным направлением осей Ох, Оу и Oz. Если даны точки 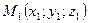 и
и 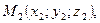 то проекции вектора
то проекции вектора 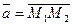 на координатные оси находятся по формулам:
на координатные оси находятся по формулам:
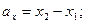
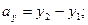
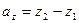 (2)
(2)
Тогда
 (3)
(3)
Подставив в (3) координаты точек A и В, получим вектор 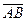

Аналогично, подставляя в (3) координаты точек А и С, находим
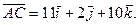
Подставив в (3) координаты точек А и D, находим вектор 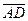 :
:
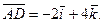
Если вектор  задан формулой (1), то его модуль вычисляется по формуле
задан формулой (1), то его модуль вычисляется по формуле
 (4)
(4)
Применяя (4), получим модули найденных векторов:
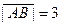
 ,
, 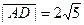
2. Косинус угла между двумя векторами равен скалярному произведению этих векторов, деленному на произведение их модулей. Находим скалярное произведение векторов 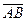 и
и  :
:
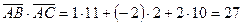
Модули этих векторов уже найдены: 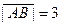 ,
,  Следовательно,
Следовательно,

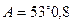 ¢.
¢.
3. Проекция вектора 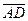 на вектор
на вектор 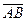 равна скалярному произведению этих векторов, деленному на модуль вектора
равна скалярному произведению этих векторов, деленному на модуль вектора 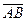 :
:
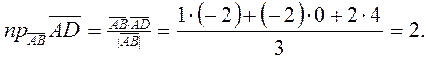
4. Площадь грани ABC равна половине площади параллелограмма, построенного на векторах 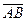 и
и  . Обозначим векторное произведение вектора
. Обозначим векторное произведение вектора 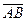 на вектор
на вектор  через вектор
через вектор  . Тогда, как известно, модуль вектора
. Тогда, как известно, модуль вектора  выражает собой площадь параллелограмма, построенного на векторах
выражает собой площадь параллелограмма, построенного на векторах 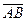 и
и  , а площадь грани ABC будет равна половине модуля вектора
, а площадь грани ABC будет равна половине модуля вектора  :
:
_


 кв. ед.
кв. ед.
5. Объем параллелепипеда, построенного на трех некомпланарных векторах, равен абсолютной величине их смешанного произведения. Вычислим смешанное произведение 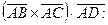
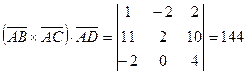
Следовательно, объем параллелепипеда равен 144 куб. ед., а объем заданной пирамиды ABCD равен 24 куб. ед.
3. 3 Вопросы для самопроверки.
- Дайте определение вектора.
- Какие векторы называются равными?
- Геометрическое и аналитическое толкование координат вектора.
- Запишите модуль вектора между координатами.
- Как выполняется сложение, вычитание, умножение вектора на число геометрически (рисунком) и аналитически (формулой).
- Дайте определение базису пространства.
- Запишите скалярное произведение двух векторов в векторной форме и между координатами перемножаемых векторов. То же для векторного и смешанного произведения.
- Условия коллинеарности и компланарности векторов в векторной и координатной форме.
Тема 4. Введение в анализ.
Пискунов, гл 1, § 1-9, упр 1-9, 39, 40
Гл 2, § 1-5, упр 1-6, 9-29, § 6-8,
Упр 31-35, 41-48, § 9, 10, упр 57-59
§ 11, упр 60-62.
4.1 Понятие предела.
Определение. Число а называется пределом функции y =f(x) в т.  если для любого сколько угодно малого наперёд заданного ε>0 найдётся такое δ>0 (δ=δ(ε)), что выполняется неравенство
если для любого сколько угодно малого наперёд заданного ε>0 найдётся такое δ>0 (δ=δ(ε)), что выполняется неравенство 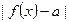 <e при
<e при  <
< 
Этот факт записывается так: 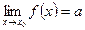
Если 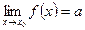 , то говорят, что функция имеет пределом число a на бесконечности (x→∞).
, то говорят, что функция имеет пределом число a на бесконечности (x→∞).
Если  , то функцию
, то функцию 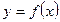 называют бесконечно большой величиной в окрестности т.
называют бесконечно большой величиной в окрестности т. 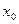 .
.
Если  , то f(x)- бесконечно большая величина на бесконечности (x→∞).
, то f(x)- бесконечно большая величина на бесконечности (x→∞).
Если  , то
, то 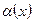 - бесконечно малая функция (величина) в окрестности т. X0.
- бесконечно малая функция (величина) в окрестности т. X0.
Если  , то
, то 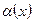 - бесконечно малая величина на бесконечности (x→∞).
- бесконечно малая величина на бесконечности (x→∞).
При вычислении пределов используются теоремы о пределах, а также 1-ый замечательный предел 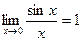
второй замечательный предел 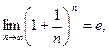
 , а также формулы
, а также формулы 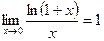 ,
, 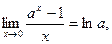
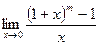
4.2 Способы раскрытия неопределённостей вида 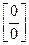 и
и 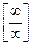 .
.
I. Если  то можно использовать три способа раскрытия этой неопределённости.
то можно использовать три способа раскрытия этой неопределённости.
1-ый способ. Разложить и числитель и знаменатель дроби на множители, затем сократить на общий множитель.
|
|
|
|
|
Дата добавления: 2014-11-16; Просмотров: 723; Нарушение авторских прав?; Мы поможем в написании вашей работы!