
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Указания к выполнению контрольной работы №1
|
|
|
|
(темы 1-6)
Тема 1. Решение систем линейных уравнений.
Данко, гл 4,§1-7
Лихолетов, ч I гл. 7, §58-61.
1.1 Системы двух уравнений 1-ой степени с двумя переменными. Определители 2-го порядка.
Пусть требуется решить систему
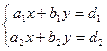 (1)
(1)
После исключения переменной y из уравнений получим 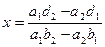 (2).
(2).
После исключения переменной x из уравнений получим 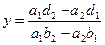 (3)
(3)
Если знаменатель 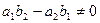 , то система (1) имеет единственное решение, которое находится по формулам (2),(3).
, то система (1) имеет единственное решение, которое находится по формулам (2),(3).
Если принять обозначения:
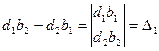

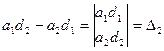
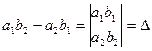 , то решение системы примет вид:
, то решение системы примет вид: 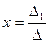 ,
, 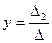 (4)
(4)
, где 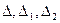 - определители системы,
- определители системы, 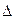 - главный определитель.
- главный определитель.
Определитель- таблица, составленная из коэффициентов при неизвестных и свободных членов системы (1).
Определитель, имеющий две строки и два столбца называется определителем 2-го порядка. Формулы (4) называются формулами Крамера.
Вычисление определителей второго порядка:
(+)
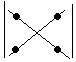
(-)
Пример: 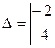
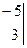 =(-2·3)-(4·(-5))= -6+20=14,
=(-2·3)-(4·(-5))= -6+20=14, 
1.2 Вычисление определителей 3-го порядка. Правило треугольников.
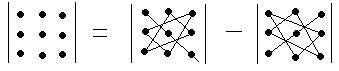 , т. е
, т. е
Определитель 3-го порядка равен сумме произведений трёх элементов, взятых по одному из каждой строки и каждого столбца.
Пример. 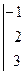
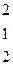
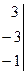 = ((-1)·1·(-1)+2·2·3+2·(-3)·3)-(3.1·3+2·2·(-1)+2·(-3)·(-1))= (1+12-18)- (9-4+6)=
= ((-1)·1·(-1)+2·2·3+2·(-3)·3)-(3.1·3+2·2·(-1)+2·(-3)·(-1))= (1+12-18)- (9-4+6)=
= (-5)-11= -16.
1.3 Разложение определителя по элементам 1-ой строки.
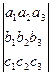 =
= 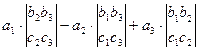
т.е значение определителя равно произведению элементов 1-ой строки на соответствующие определители 2-го порядка, полученные после вычёркивания i -той строки и k -того столбца, на пересечении которых находится соответствующий элемент, причём a1 берётся со своим знаком, a2 -c противоположным, a3 - со своим знаком.
Пример: Вычислить определитель.
 |  |
-1 2 3
2 1 –3 = -1 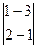 -2
-2 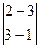 +3
+3 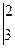
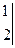 = -1·(-1+6)-2(-2+9)+3(4-3)= -1·5-2·7+3·1= -16
= -1·(-1+6)-2(-2+9)+3(4-3)= -1·5-2·7+3·1= -16
3 2 -1
Замечание. Разложение можно выполнять по элементам любой строки (столбца).
Задача. Решить систему 
Решение: Составим главный определитель системы из коэффициентов при неизвестных и вычислим его:
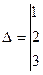
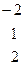
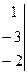 = 1·
= 1· 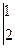
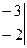 - (-2)
- (-2) 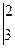
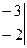 +1·
+1· 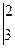
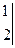 = (-2+6)+2(-4+9)+1(4-3)=4+10+1=15
= (-2+6)+2(-4+9)+1(4-3)=4+10+1=15
Составим вспомогательный определитель 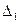 . Он получается из главного путём замены первого столбца свободными членами.
. Он получается из главного путём замены первого столбца свободными членами.
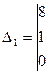
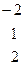
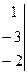 = 8·
= 8· 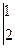
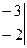 +2
+2 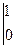
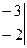 +1
+1 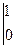
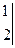 = 8(-2+6)+2 (-2-0)+1(2-0)=8·4+2·(-2)+2=30
= 8(-2+6)+2 (-2-0)+1(2-0)=8·4+2·(-2)+2=30
Составим определитель 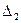 , путём замены 2-го столбца (в главном определителе) свободными членами.
, путём замены 2-го столбца (в главном определителе) свободными членами.
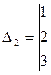
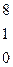
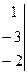 = - 45 Вычислить самостоятельно.
= - 45 Вычислить самостоятельно.
Составим определитель  путём замены 3-го столбца (в главном определителе) свободными членами.
путём замены 3-го столбца (в главном определителе) свободными членами.
 =
= 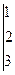
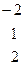
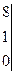 =0 Вычислить самостоятельно.
=0 Вычислить самостоятельно.
Тогда по правилам Крамера имеем
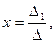
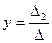 ,
, 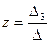 или
или 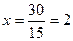 ,
, 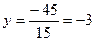 ,
, 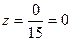
Сделать проверку самостоятельно.
Ответ: x=2, y= -3, z =0
1.4 Решение систем линейных уравнений методом Гаусса.
Пусть дана система 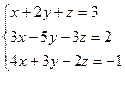 (1)
(1)
Гаусс при решении системы использовал метод исключения неизвестных. В результате исходная система приводится к треугольному виду:


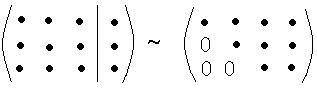
В этих таблицах, называемых матрицами, должны быть записаны коэффициенты при неизвестных, а после вертикальной черты-свободные члены.
В системе (2) из последнего уравнения находится неизвестное z, из 2-го-другое неизвестное y, из 1-го- первое неизвестное x.
Задача. Решить систему.

|
|
|
|
|
Дата добавления: 2014-11-16; Просмотров: 415; Нарушение авторских прав?; Мы поможем в написании вашей работы!