Пример. Ответ: где 2- предельное значение аргумента, (-1) -

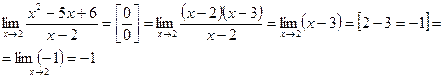
Ответ: где 2- предельное значение аргумента, (-1) -

предельное значение функции y.

2-ой способ. Использовать правило Лопиталя, т.е использовать равенство:

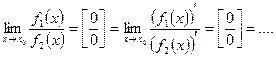
Пример: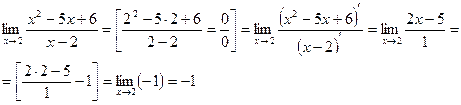

3-ий способ. Применить таблицу эквивалентности бесконечно малых.

Таблица.

1.

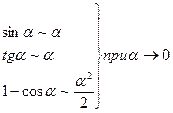
2.

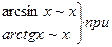
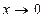
3.

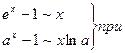
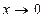
4.

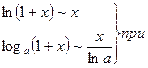
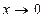
Пример: Найти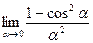

Решение.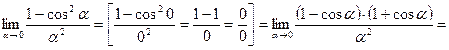

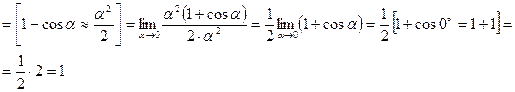II. Если 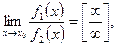то можно использовать три способа раскрытия этой неопределённости.

1-ый способ. Использовать правило Лопиталя.

Пример. Найти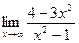

Решение: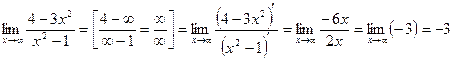

2-ой способ. Разделить все слагаемые числителя и все слагаемые знаменателя на старшую переменную дроби.

Пример. Найти 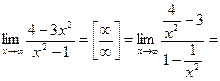[ 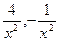-бесконечно малые величины ]=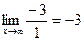

Ответ: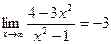

4.2 Первый и второй замечательные пределы.

1. 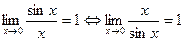- первый замечательный предел.

Замечание. При x®0 sin x~ x

Пример 1.

Найти

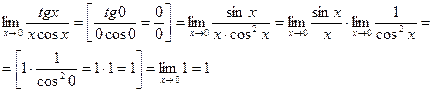
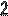
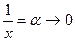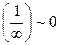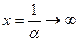если заменить , т.к , то

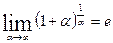
Заметим,что показатель степени обратен по величине второму слагаемому в основании.

Пример 2. 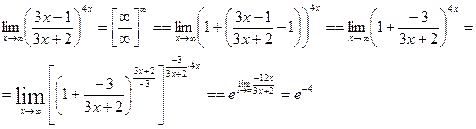представили основание в виде суммы 1 и некоторой бесконечно малой величины.

Выполненные тождественные преобразования в показателе степени, позволяют выделить 2-ой замечательный предел. (в квадратных скобках)

4.3 Непрерывность функции. Точки разрыва.

Определение 1. Функция 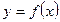называется непрерывной в точке x₀, если выполняется равенство: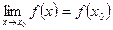

Определение 2. Функция 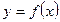называется непрерывной в точке x₀, если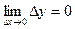

где 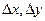соответственно приращение аргумента и приращение функции.

Пример. Дана функция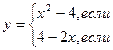

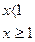
Требуется: 1). Найти точку разрыва данной функции.

2). Найт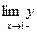и и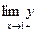

3). Найти скачок функции в точке разрыва.

Решение.

Данная функция определена и непрерывна в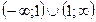

При x=1 функция терпит разрыв, т.к меняется аналитическое выражение функции.

y

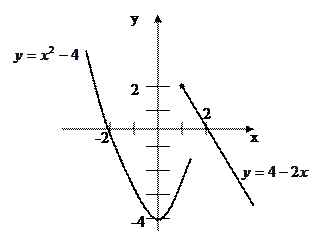
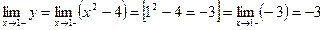
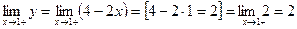
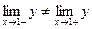
x=1- точка разрыва первого рода.

Скачком функции называется абсолютная величина разности между её правым и левым предельными значениями т.е 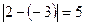(ед). –скачок функции.

4.4 Вопросы для самопроверки.

1. Дайте определение функции, области определения. Приведите примеры.

2. Сформулируйте определение предела функции в точке.

3. Какая переменная величина называется бесконечно малой? Бесконечно большой в точке 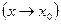и на бесконечности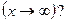

4. Что означают выражения: 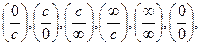где C-const?

5. Приведите пример бесконечно малой функции в т. x=2 и бесконечно большой функции в этой же точке (аналитический и графический).

6. Каким свойством обладает приращение аргумента и приращение функции, если функция непрерывна в точке x₀ ?

Дата добавления: 2014-11-16