Четные и нечетные функции

Преобразование графиков.

Словесное описание функции.

Графический способ.

Графический способ задания функции является наиболее наглядным и часто применяется в технике. В математическом анализе графический способ задания функций используется в качестве иллюстрации.

Графиком функции f называют множество всех точек (x;y) координатной плоскости, где y=f(x), а x «пробегает» всю область определения данной функции.

Подмножество координатной плоскости является графиком какой-либо функции, если оно имеет не более одной общей точки с любой прямой, параллельной оси Оу.

Пример. Является ли графиками функций фигуры, изображенные ниже?

Преимуществом графического задания является его наглядность. Сразу видно, как ведёт себя функция, где возрастает, где убывает. По графику сразу можно узнать некоторые важные характеристики функции.

Вообще, аналитический и графический способы задания функции идут рука об руку. Работа с формулой помогает построить график. А график частенько подсказывает решения, которые в формуле и не заметишь.

Почти любой ученик знает три способа задания функции, которые мы только что рассмотрели.

Попытаемся ответить на вопрос: "А существуют ли другие способы задания функции?"

Такой способ есть.

Функцию можно вполне однозначно задать словами.

Например, функцию у=2х можно задать следующим словесным описанием: каждому действительному значению аргумента х ставится в соответствие его удвоенное значение. Правило установлено, функция задана.

Более того, словесно можно задать функцию, которую формулой задать крайне затруднительно, а то и невозможно.

Например: каждому значению натурального аргумента х ставится в соответствие сумма цифр, из которых состоит значение х. Например, если х=3, то у=3. Если х=257, то у=2+5+7=14. И так далее. Формулой это записать проблематично. А вот табличку легко составить.

Способ словесного описания - достаточно редко используемый способ. Но иногда встречается.

Если есть закон однозначного соответствия между х и у - значит, есть функция. Какой закон, в какой форме он выражен - формулой, табличкой, графиком, словами – сути дела не меняет.

Рассмотрим функции, области определения которых симметричны относительно начала координат, т.е. для любого х из области определения число (- х) также принадлежит области определения. Среди таких функций выделяют четные и нечетные.

Определение. Функция f называется четной, если для любого х из ее области определения

Пример. Рассмотрим функцию

Она является четной. Проверим это.

Область определения вся числовая ось, а значит, она симметрична относительно точки (0;0).

Для любого х выполнены равенства

Таким образом, у нас выполняются оба условия, значит функция четная. Ниже представлен график этой функции.

Определение. Функция f называется нечетной, если для любого х из ее области определения

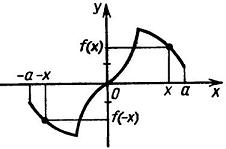
Пример. Рассмотрим функцию

Она является нечетной. Проверим это.

Область определения вся числовая ось, а значит, она симметрична относительно точки (0;0).

Для любого х выполнены равенства

Таким образом, у нас выполняются оба условия, значит функция нечетная. Ниже представлен график этой функции.

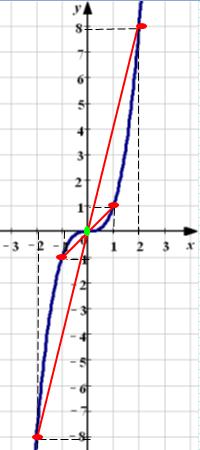
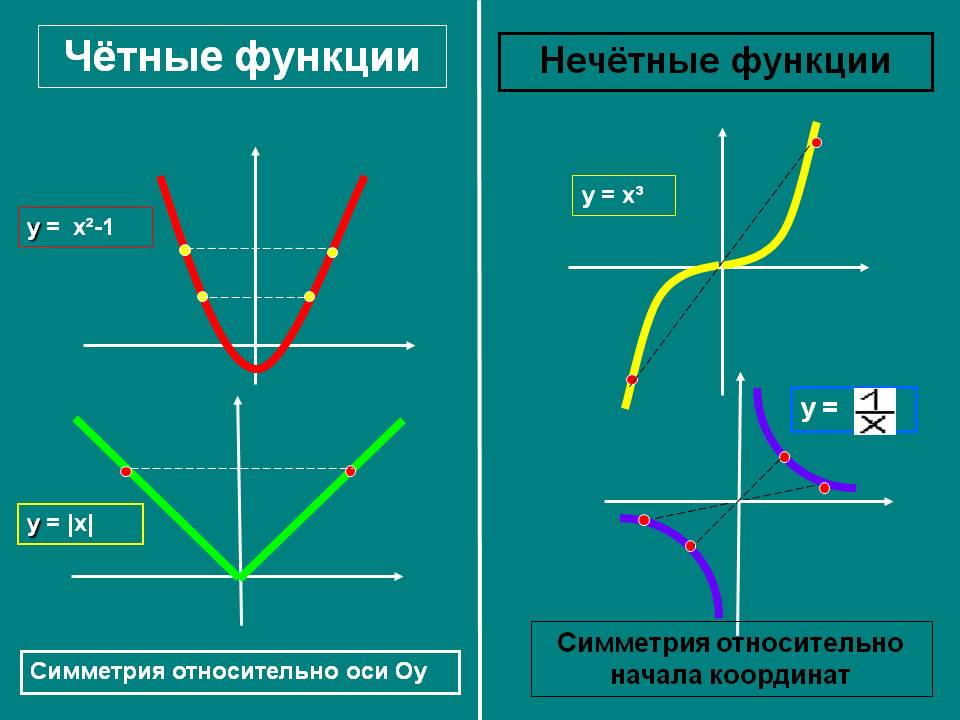
Графики, изображенные на первом и третьем рисунках симметричны относительно оси ординат, а графики, изображенные на втором и четвертом рисункам симметричны относительно начала координат.

Какие из функций, графики которых изображены на рисунках являются четными, а какие нечетными?

Укажите какие из функций, графики которых изображены ниже, являются четнымиа какие нечетными:

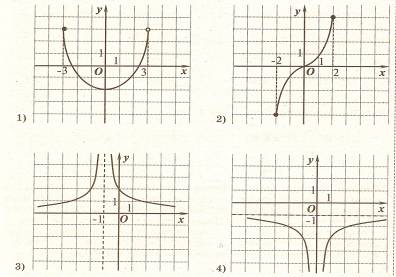
Укажите какие из функций, графики которых изображены ниже, являются четными:

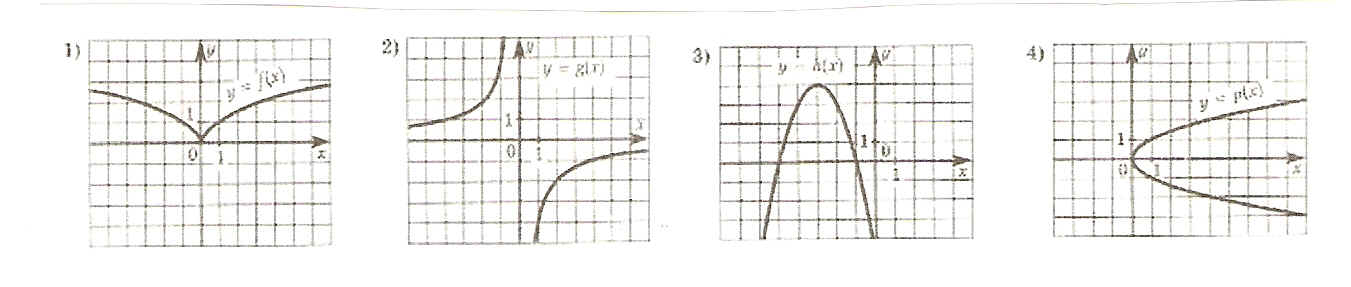
Укажите какие из функций, графики которых изображены ниже, являются нечетными:

Достроить график функции f(x) на промежутке (- ∞; 0), зная, что f(x) – нечётная функция и на промежутке [0; +∞) её график имеет вид:

Достроить график функции f(x) на промежутке (- ∞; 0), зная, что f(x) – нечётная функция и на промежутке [0; +∞) её график имеет вид:

Дата добавления: 2014-11-16