РЕШЕНИЕ. Даны следующие константы и матрицы:

РЕШЕНИЕ

РЕШЕНИЕ

Вычислить матрицу

УСЛОВИЕ

ДОМАШНЯЯ КОНТРОЛЬНАЯ РАБОТА №1 ПО МАТЕМАТИКЕ.

РАЗДЕЛ 1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ

Даны следующие константы и матрицы: ,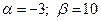

, , , .

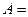
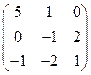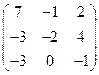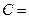
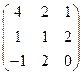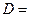
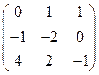ЗАДАНИЕ 1

.

Найдём матрицу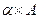

.

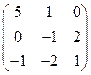
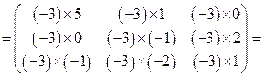
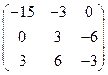
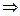
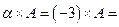
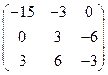Вычислим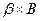

.

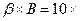
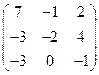
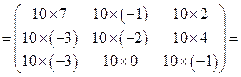
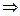
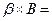
Найдём сумму матриц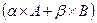

.

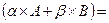
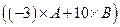
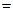
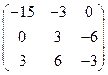
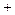
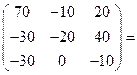
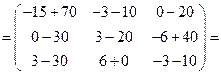
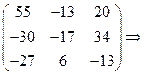
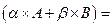
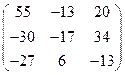Транспонируем матрицу :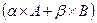

.

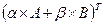
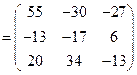Найдём матрицу .

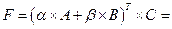
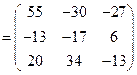
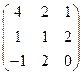
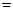
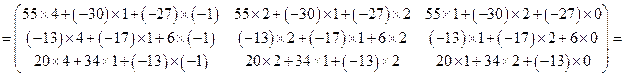
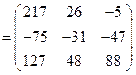
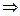
Следовательно, искомая матрица есть

.

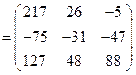ЗАДАНИЕ 2

Найти произведение матриц:

.

.

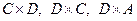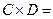
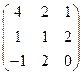
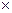
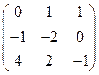
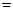
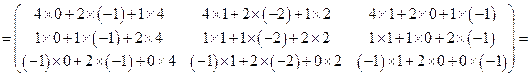
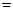
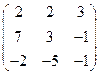То есть,

.

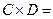
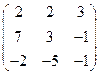Аналогично, найдём иные произведения матриц.

.

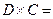
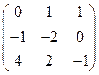
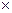
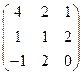
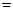
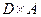
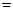
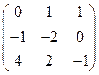
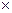
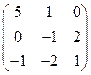
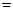
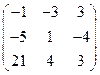ЗАДАНИЕ 3

Рассчитать:

а) рассчитать значения определителя для матрицы ,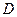

б) вычислить определитель матрицы разложением по элементам строки или столбца для матрицы ,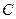

в) найти обратные матрицы для матриц ,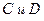

г) найти ранг матриц ,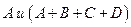

, , , .

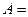
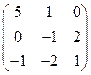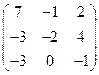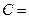
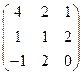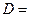
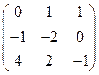а) Рассчитаем значения определителя для матрицы .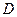

.

.

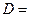
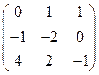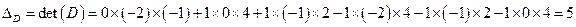То есть, определитель матрицы 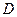равен 5.

б) Вычислим определитель матрицы разложением по элементам строки или столбца для матрицы .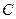

.

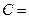
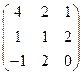Вторую строку умножим на 4 и вычтем из первой строки. Вторую строку сложим с третьей строкой. Вычёркиваем вторую строку и первый столбец.

.

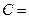
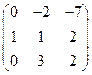Тогда, определитель рассчитывается

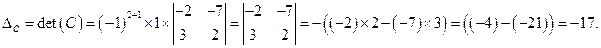
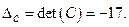
в) Найдём обратную матрицу для матрицы .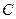

Имеем матрицу

.

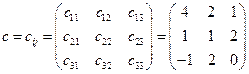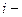номер строки, 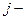номер столбца.

Найдём матрицу 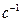обратную к исходной матрице .

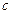Сначала найдём транспонированную матрицу 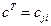к исходной матрице .

.

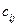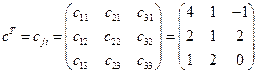Найдём алгебраические дополнения элементов транспонированной матрицы.

.

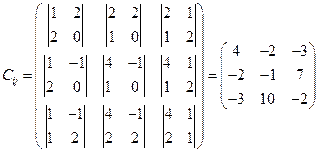Обратная матрица есть

.

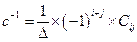Определитель матрицы нашли выше

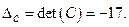
Тогда, получим.

.

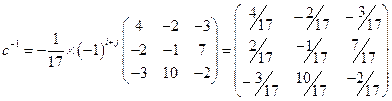Таким образом, матрица обратная матрице 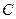имеет вид:

.

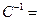
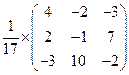Найдём обратную матрицу для матрицы .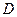

.

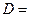
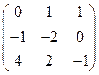Сначала найдём транспонированную матрицу 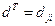к исходной матрице .

.

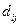Найдём алгебраические дополнения элементов транспонированной матрицы.

.

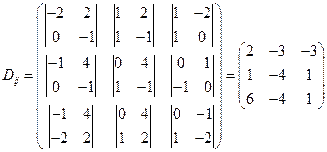Обратная матрица есть

.

Определитель матрицы нашли выше

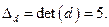
Тогда, получим.

.

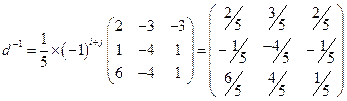Таким образом, матрица обратная матрице 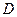имеет вид:

.

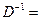
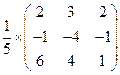г) Найдём ранг матрицы 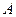. Проведём преобразования Гаусса и определим число линейно независимых строк.

.

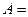
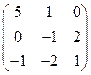Третью строку умножим на -1 и переставим с первой строкой. Получим.

.

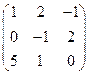Первую строку умножим на 5 и вычтем из третьей строки. Получим.

.

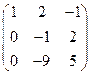Вторую строку умножим на -1. Получим.

.

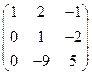Вторую строку умножим на 2 и вычтем из первой строки. Вторую строку умножим на 9 и сложим с третьей строкой. Получим.

.

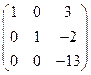Третью строку разделим на -13. Получим.

.

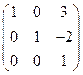Третью строку умножим на 3 и вычтем из первой строки. Третью строку умножим на 2 и сложим со второй строкой. Получим.

.

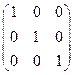Таким образом, исходную матрицу привели к диагональному виду. Получили, что имеется три линейно независимых строк. Следовательно, ранг матрицы 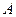равен 3.

.

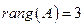Найдём ранг матрицы .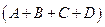

.

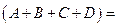
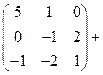
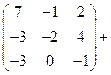
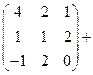
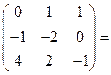
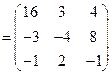Проведём преобразования Гаусса и определим число линейно независимых строк.

.

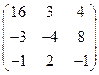Третью строку умножим на -1 и переставим её с первой строкой. Получим.

.

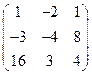Первую строку умножим на 3 и сложим её со второй строкой. Первую строку умножим на 16 и вычтем из третьей строки. Получим.

.

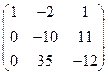Вторую строку разделим на – 10, получим.

.

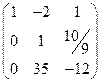Вторую строку умножим на 2 и сложим с первой строкой. Вторую строку умножим на 35 и вычтем из третьей строки. Получим.

.

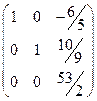Третью строку разделим на 53/2, получим.

.

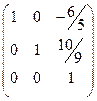Третью строку умножим на 6/5 и сложим с первой строкой. Третью строку умножим на 10/9 и вычтем из второй строки. Получим.

.

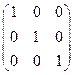Получили, что имеется три линейно независимых строки. Следовательно, ранг матрицы 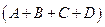равен трём.

.

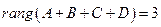ЗАДАНИЕ 4.

Решить систему линейных уравнений по формулам Крамера. Сделать проверку.

.

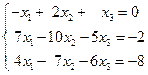Дата добавления: 2014-11-16