Решение. 1. Сечение составлено из стандарт­ных профилей, главные центральные моменты инерции которых приводятся в таблицах ГОСТ

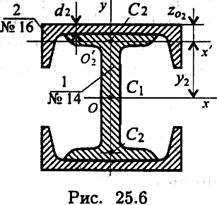1. Сечение составлено из стандарт­ных профилей, главные центральные моменты инерции которых приводятся в таблицах ГОСТ, см. Приложение 1. Для двутавра № 14 по ГОСТ 8239-89 Jox 1 = 572 см⁴.

Для швеллера № 16 по ГОСТ 8240-89 Jox ₂ = 757 см⁴.

Площадь А₂ = 18,1см², Jo_y2 = 63,3см⁴.

2. Определяем координату центра тяжести швеллера относи­тельно оси Ох. В заданном сечении швеллер повернут и поднят. При этом главные центральные оси поменялись местами.

у₂ = (h₁/2) + d₂ — zo₂, по ГОСТ находим h₁ = 14 см; d₂ = 5 мм; z_o = 1,8 см.

Момент инерции сечения равен сумме моментов инерции швеллеров и двутавра относительно оси Ох. Используем формулу моментов инерции относительно параллельных осей:

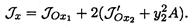
В данном случае

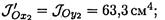
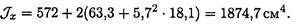
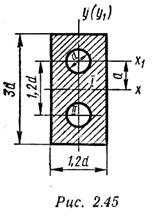
Пример 3. Для заданного сечения (рис. 2.45) вычислить главные центральные моменты инерции.

Решение

Сечение имеет две оси симметрии, которые являются его главными центральными осями.

Разбиваем сечение на две про­стейшие фигуры: прямоугольник (I) и два круга (II).

Момент инерции сечения относи­тельно оси х

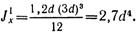
где

Ось x (центральная ось сечения) не является централь­ной осью круга. Следовательно, момент инерции круга следует вычислять по формуле

где

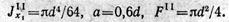
Подставляя значения J_x^’’, a, F" в формулу, получаем

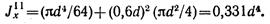
Тогда

Ось у является центральной для прямоугольника и кругов. Следовательно,

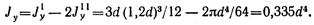
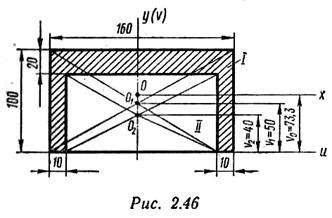Пример 4. Для заданного сечения (рис.2.46)определить положение главных центральных осей и вы­числить главные центральные моменты инерции.

Дата добавления: 2014-11-18