
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Электрические фильтры. Линии с распределёнными параметрами. 2 страница
|
|
|
|
| 4,28 | 1,75 | 0,922 | 50,7 | 38,6 | 3.2, г | 3.3 | |
| 2,02 | 1,12 | 0,505 | 3.2, а | 3.9 | |||
| 3,5 | 1,2 | 0,667 | 8,52 | 41,4 | 3.2, б | 3.10 | |
| 1,25 | 2,09 | 3.2, в | 3.5 | ||||
| 5,75 | 1,15 | 0,72 | 39,2 | 86,5 | 3.2, в | 3.6 |
Указание:
На примере рисунков 3.9 и 3.10 покажем, как осуществляется разложение в ряд Фурье кривых, которые имеют постоянную составляющую, и начало которых сдвинуто во времени по отношению к табличным кривым. Прежде всего, выделим в напряжении u 1(t) (рисунок 3.10) постоянную составляющую Um/ 2 и мысленно проведем новую ось времени на высоте Um/ 2. Тогда относительно новой оси времени оставшуюся часть напряжения запишем в виде
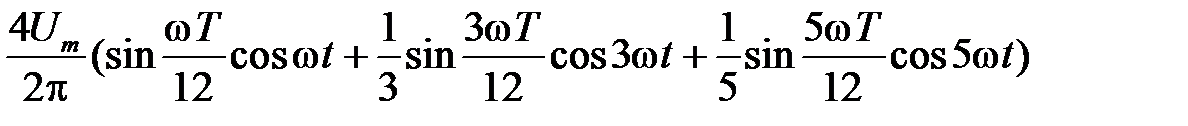
Здесь под Um понимается амплитуда заданного напряжения u 1(t), а угол ω T /12 равен углу, обозначенному в учебниках α. С учетом постоянной составляющей u 1(t) (рисунок 3.10) раскладывается в ряд Фурье следующим образом:

График напряжения u 1(t) (рисунок 3.9) на время T /4 смещен (запаздывает) во времени, поэтому для графика, представленного на рисунке 3.9:
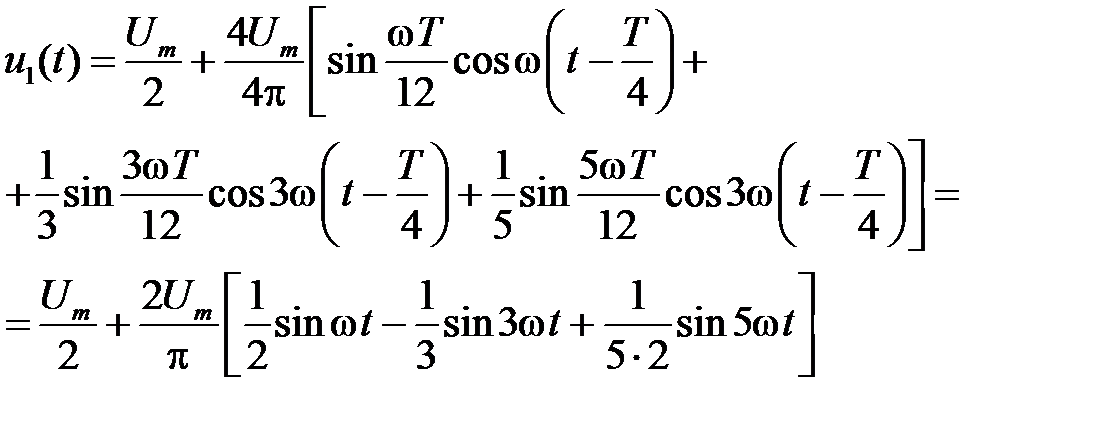
Покажем, как вывести формулу напряжения на выходе схемы 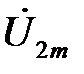 через параметры схемы и напряжение на входе
через параметры схемы и напряжение на входе 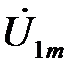 . Исходя из первого уравнения четырехполюсника, написанного в A-форме, получим
. Исходя из первого уравнения четырехполюсника, написанного в A-форме, получим
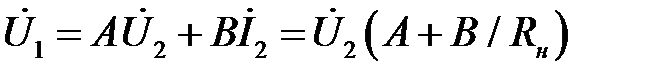 .
.
Отсюда
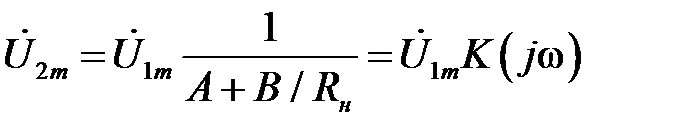 ,
,
где 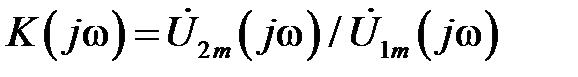 - передаточная функция четырехполюсника на частоте ω
- передаточная функция четырехполюсника на частоте ω
Для рисунка 3.11: 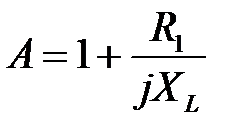 ;
; 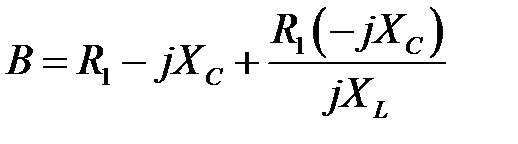
После небольших преобразований получим:

Задача 3.3. Электрические фильтры.
Рассматривая схемы, показанные на рисунке 3.2, как схемы фильтров, работающих на согласованную нагрузку:
1) определить значения граничных частот полосы прозрачности фильтра (частот среза);
2) качественно построить зависимость характеристического сопротивления Z с, затухания а и сдвига по фазе b в функции частоты ω;
3) на вход низкочастотного фильтра подать 1-ю гармонику напряжения u 1 из п. 1 задачи 3.2, на вход высокочастотного фильтра − 3-ю гармонику этого напряжения. Для указанной гармоники входного напряжения определить числовые значения постоянной передачи g = а + jb, характеристического сопротивления Z с, напряжений и токов во всех ветвях схемы и построить по ним векторные диаграммы токов и напряжений фильтра.
Задача 3.4. Установившиеся процессы в линии с распределёнными параметрами.
По заданным в таблице 3.3 параметрам линии (R 0; L 0; G 0; С 0), частоте f, длине линии l, комплексным значениям напряжения 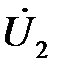 и
и 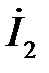 в конце линии, сопротивлению нагрузки Zн требуется:
в конце линии, сопротивлению нагрузки Zн требуется:
1.Рассчитать напряжение 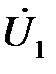 и ток
и ток  в начале линии, активную Р и полную S мощности в начале и конце линии, а также КПД линии.
в начале линии, активную Р и полную S мощности в начале и конце линии, а также КПД линии.
2.Полагая, что линия п. 1 стала линией без потерь (R 0 = G 0 =0), а нагрузка на конце линии стала активной и равной модулю комплексной нагрузки в п.1, определить напряжение 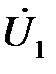 и ток
и ток  , в начале линии, а также длину электромагнитной волны λ.
, в начале линии, а также длину электромагнитной волны λ.
3.Для линии без потерь п. 2 построить график распределения действующего значения напряжения вдоль линии в функции координаты у.
Таблица 3.3
| Вари- ант | f, Гц | l, км | R, Ом/км | C 0, 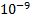 Ф/км
Ф/км
| L 0, 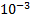 Гн/км
Гн/км
| G 0, 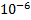 См/км
См/км
| 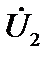 ,
B ,
B
| 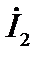 ,
мА ,
мА
| Zн, Ом |
| 9,6 | 5,08 | 1,25 | 64,2 е j 15° | — | |||||
| 11,8 | 4,16 | 0,75 | — | 21,1 е j 10°55' | 1188 е − j 10°55' | ||||
| 11,65 | 5,75 | 4,24 | 0,51 | 34,4 | — | 1720 е − j 6°10' | |||
| 23,7 | 78,6 | 11,5 | 1,75 | — | 10 е j 13°12' | 1965 е − j 13°12' | |||
| 10,6 | 4,6 | 0,175 | — | ||||||
| 4,1 | 1,25 | — | |||||||
| 12,6 | 12,7 | 3,85 | 0,8 | — | 1270 е – j 20° | ||||
| 16,3 | 6,11 | 5,7 | 2,25 | — | 23,9 е j 14°18' | 512 е – j 14°18' | |||
| 12,4 | 4,8 | 1,6 | — | 355 е – j 8°50' | |||||
| 2,9 | 3,8 | 0,7 | — | 18 е j 7°50' | 278 е – j 7°50' | ||||
| 0,65 | 84,7 | — | 1620 е – j 12°25' | ||||||
| 9,6 | 14,8 | 10,8 | 0,725 | — | 12,2 е j 8°12' | 1800 е – j 8°12' | |||
| 12,7 | 97,2 | 6,4 | 7,5 | 0,82 | — | ||||
| 4,2 | 6,4 | 3,3 | — | 16,3 е j 15°22' | 800 е – j 15°22' | ||||
| 64,8 | 25,2 | 3,6 | 6,7 | — | 690 е – j 7°45' | ||||
| 42,7 | 16,7 | 2,66 | 1,5 | — | 13,1 | ||||
| 47,1 | 6,8 | 7,08 | 1,9 | — | 2000 е – j 16°15' | ||||
| 8,2 | 10,4 | 0,46 | — | 20 е j 5°12' | 400 е – j 5°12' | ||||
| 92,3 | 20,4 | 3,4 | 7,08 | 0,9 | 33,9 | — | 1060 е – j 7°15' | ||
| 29,2 | 8,2 | 6,08 | 0,675 | — | 33,3 е j 23°10' | 1800 е – j 23°10' | |||
| 4,8 | 10,16 | 0,625 | — | 32,1 е j 15° | 3120 е – j 15° | ||||
| 11,8 | 4,16 | 1,5 | — | 1188 е – j 10°55' | |||||
| 11,5 | 4,24 | 0,51 | — | 10 е j 6°10' | 1220 е − j 6°10' | ||||
| 11,85 | 157,2 | 11,5 | 3,5 | 78,6 | — | 1965 е – j 13°12' | |||
| 5,3 | 9,2 | 0,0875 | — |
Продолжение таблицы 3.3
| 4,1 | 2,5 | — | |||||||
| 50,4 | 3,175 | 3,85 | 0,8 | — | 1,97 е j 20° | 2540 е – j 20° | |||
| 22,55 | 12,22 | 1,9 | 2,25 | — | 209,5 е – j 14°18' | ||||
| 24,8 | 9,6 | 0,8 | — | 56,4 е j 8°50' | 710 е – j 8°50' | ||||
| 157,5 | 5,8 | 3,8 | 1,4 | — | 278 е – j 7°50' | ||||
| 5,5 | 0,65 | — | 26,05 е j 12°25' | 1150 е – j 12°25' | |||||
| 19,2 | 14,8 | 10,8 | 1,55 | — | 1800 е – j 8°12' | ||||
| 12,7 | 194,4 | 3,2 | 0,41 | — | |||||
| 14,9 | 2,8 | 8,54 | 2,1 | 25,4 | 24,5 е j 15°22' | — | |||
| 91,5 | 12,6 | 7,2 | 6,7 | — | 22,5 е j 7°45' | 490 е – j 7°45' | |||
| 21,35 | 33,4 | 2,66 | — | ||||||
| 47,1 | 3,4 | 14,16 | 0,95 | — | 6 е j 16°15' | 4000 е – j 16°15' | |||
| 11,5 | 8,2 | 10,4 | 0,92 | — | 400 е – j 5°12' | ||||
| 10,2 | 6,8 | 7,08 | 0,9 | — | 16 е j 7°15' | 750 е – j 7°15' | |||
| 14,6 | 8,2 | 3,04 | 0,675 | 42,3 | — | 1255 е – j 23°10' | |||
| 4,8 | 5,08 | 0, 675 | 70,5 | — | 2200 е – j 15° | ||||
| 5,9 | 8,32 | 0,75 | — | 42,2 е j 10°55' | 2376 е – j 10°55' | ||||
| 7,5 | 11,5 | 4,24 | 1,02 | 48,8 | — | 1220 е – j 6°10' | |||
| 23, 7 | 78,6 | 8,1 | 7,05 | 1,75 | — | 14,2 е j 13°12' | 1965 е – j 13°12' | ||
| 103,5 | 5,3 | 4,6 | 0,0875 | — | 560,4 | ||||
| 8,2 | 1,25 | — | |||||||
| 75,6 | 9,52 | 11,55 | 1,2 | — | 2540 е – j 20° | ||||
| 14,2 | 180,4 | 6,11 | 7,6 | 2,25 | 23,9 е j 14°18' | 590 е – j 14°18' | |||
| 12,4 | 4,8 | 0, 8 | 28, 2 | — | 500 е – j 8°50' | ||||
| 157,5 | 11,6 | 6,5 | 7,6 | 0,7 | -— | 36 е j 7°50' | 556 е – j 7°50' | ||
| 1,3 | — | 1150 е – j 12°25' | |||||||
| 14,4 | 7,4 | 8,1 | 0,725 | — | 24,4 е j 8°12' | 2205 е – j 8°12' | |||
| 97,2 | 3,2 | 7,5 | 0,41 | 42,3 | — | ||||
| 5,6 | 8,54 | 2,1 | — | 12,25 е j 15°22' | 800 е – j 15°22' | ||||
| 45,75 | 25,2 | 7,2 | 6, 7 | — | 490 е – j 7°45' | ||||
| 21,35 | 66,8 | 9,5 | 5,32 | 1,5 | — | 26,2 | |||
| 66,7 | 3,4 | 7,08 | 0,95 | 16,9 | — | 2820 е – j 16°15' | |||
| 18,4 | 4,1 | 7,8 | 0,46 | — | 40 е j 5°12' | 500 е – j 5°12' | |||
| 20,4 | 6,8 | 7,08 | 1,8 | — | 750 е – j 7°15' | ||||
| 7,3 | 16,4 | 3,04 | 0,675 | 16,65 е j 23°10' | 900 е – j 23°10' | ||||
| 4,8 | 2,54 | 0,625 | 32,1 е j 15° | — | |||||
| 5,9 | 2,08 | 0,75 | 42,2 е j 10°55' | — | |||||
| 5,75 | 2,12 | 0,51 | 24,4 | 20 е j 6°10' | — | ||||
| 23,7 | 78,6 | 5,75 | 1,75 | 39,3 | 20 е j 13°12' | — | |||
| 5,3 | 2,3 | 0,0875 | — | ||||||
| 2,05 | 1,25 | ||||||||
| 50,4 | 6,35 | 7,7 | 0,8 | 3,94 е j 20° | — | ||||
| 90,2 | 6,11 | 3,8 | 2,25 | 23,9 е j 14°18' | — | ||||
| 6,2 | 2,4 | 0,8 | 56,4 е j 8°50' | — | |||||
| 2,9 | 6,5 | 1,9 | 0,7 | 36 е j 7°50' | — |
Продолжение таблицы 3.3
| 5,5 | 0,65 | 52,1 е – j 12°25' | — | |||||||
| 9,6 | 7,4 | 5, 4 | 0,725 | — | 24,4 е j 8°12' | 1800 е – j 8°12' | ||||
| 25,4 | 48,6 | 3,2 | 3,75 | 0,41 | — | |||||
| 2,8 | 4,27 | 2,1 | 24,5 е j 15°22' | — | ||||||
| 91,5 | 12,6 | 3,6 | 3,35 | 45 е j 7°45' | — | |||||
| 42,7 | 16,7 | 9,5 | 1,33 | 1,5 | 26,2 | — | ||||
| 94,2 | 3,4 | 3,54 | 0,95 | 6 е j 16°15' | — | |||||
| 4,1 | 5,2 | 0,46 | 40 е j 5°12' | — | ||||||
| 10,2 | 3,4 | 3,54 | 0,9 | — | 750 е – j 7°15' | |||||
| 7,3 | 8,2 | 1,52 | 0,675 | 33,3 е j 23°10' | — | |||||
| 9,6 | 5,08 | 0,625 | — | 16,05 е j 15° | 1560 е – j 15° | |||||
| 5,9 | 4,16 | 0,75 | 70,5 | — | 1675 е – j 10°55' | |||||
| 7,5 | 5,75 | 8,48 | 0,51 | — | 20 е j 6°10' | 2440 е – j 6°10' | ||||
| 16,75 | 157,2 | 5,75 | 1,75 | 55,4 | — | 2770 е – j 13°12' | ||||
| 10,6 | 4,6 | 0,0875 | — | |||||||
| 56,7 | 4,1 | 1,25 | 42,3 | — | ||||||
| 75,6 | 6,35 | 11,52 | 0,8 | — | 3,94 е j 20° | 3110 е – j 20° | ||||
| 180,4 | 12, 22 | 7,6 | 4,5 | — | 419 е – j 14°18' | |||||
| 6,2 | 4, 8 | 0,8 | — | 28,2 е j 8°50' | 355 е – j 8°50' | |||||
| 5,8 | 6,5 | 3,8 | 0,7 | 14,1 | — | 392 е – j 7°50' | ||||
| 0,65 | — | 52,1 е j 12°25' | 2300 е – j 12°25' | |||||||
| 19,2 | 7,4 | 10,8 | 0,725 | 24,4 е j 8°12' | — | |||||
| 25,4 | 48,6 | 6, 4 | 7,5 | 0,41 | — | 22,5 | ||||
| 10,5 | 5,6 | 8,54 | 4, 2 | — | 800 е – j 15°22' | |||||
| 45,75 | 50,4 | 3,6 | 13,4 | — | 45 е j 7°45' | 980 е – j 7°45' | ||||
| 30,2 | 33, 4 | 9,5 | 2,66 | 1,5 | 29,6 | — | ||||
| 94,2 | 6,8 | 7,08 | 0,95 | 3 е j 16°15' | 2000 е – j 16°15' | |||||
| 16, 3 | 4,1 | 10,4 | 0,46 | 22,6 | — | 565 е – j 5°12' | ||||
| 40,8 | 3,4 | 14,16 | 0,9 | — | 32 е j 7°15' | 1500 е – j 7°15' | ||||
| 14,6 | 16,4 | 3, 04 | 1,35 | — | 900 е – j 23°10' | |||||
|
|
|
|
|
Дата добавления: 2014-11-18; Просмотров: 591; Нарушение авторских прав?; Мы поможем в написании вашей работы!