
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Введение в математический анализ
|
|
|
|
Метод Крамера.
1. Составляем определитель матрицы системы, который составляют из коэффициентов системы уравнений. Для этого выписываем коэффициенты: первое уравнение системы имеет при переменной 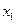 коэффициент 2, при
коэффициент 2, при 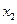 - коэффициент – (-4), при
- коэффициент – (-4), при  - коэффициент 1.
- коэффициент 1.
Записываем все эти коэффициенты в первую строку определителя основной матрицы, коэффициенты второго уравнения во вторую строку и третью соответственно.
 .
.
2. Теперь найдем: ∆ 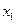 . Для этого первый столбец заменяем столбцом свободных членов.
. Для этого первый столбец заменяем столбцом свободных членов.
 .
.
3. Теперь найдем: ∆ 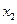 . Для этого второй столбец заменяем столбцом свободных членов.
. Для этого второй столбец заменяем столбцом свободных членов.
 .
.
4. Аналогично находим ∆  . Для этого третий столбец заменяем столбцом свободных членов.
. Для этого третий столбец заменяем столбцом свободных членов.
 .
.
5. Пользуемся формулами для нахождения неизвестных переменных

Раздел Функция.
31-40. Задана функция.
а) найдите область определения и множество значений функции;
б) исследуйте функцию на четность и нечетность.
31. 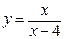 . 36.
. 36.  .
.
32. 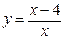 . 37.
. 37. 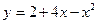 .
.
33. 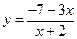 . 38.
. 38. 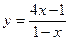 .
.
34. 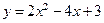 . 39.
. 39. 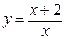 .
.
35. 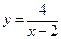 . 40.
. 40. 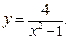
Пример. 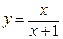 .
.
а) Найдем сначала область определения данной функции. Числитель данной дроби не содержит никаких особенностей, а вот знаменатель должен быть ненулевым. Давайте приравняем его к нулю и попытаемся найти «плохие» точки:  ,
, 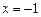 . Данное значение не входит в область определения функции. Действительно, подставьте
. Данное значение не входит в область определения функции. Действительно, подставьте 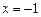 в функцию и вы увидите, что знаменатель обращается в ноль, а на ноль, как известно, делить нельзя. Таким образом, областью определения данной функции, обозначаемая
в функцию и вы увидите, что знаменатель обращается в ноль, а на ноль, как известно, делить нельзя. Таким образом, областью определения данной функции, обозначаемая  , будет
, будет 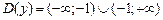 .
.
Теперь найдем множество значений данной функции. Как нетрудно убедиться, исходную функцию можно переписать в виде:  ,график которой можно получить из графика функции
,график которой можно получить из графика функции 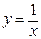 следующими преобразованиями: сдвигом на 1 единицу влево, симметричным отображением относительно O x и сдвигом на 1 единичный отрезок вверх по оси O y. Таким образом, областью значений данной функции будет
следующими преобразованиями: сдвигом на 1 единицу влево, симметричным отображением относительно O x и сдвигом на 1 единичный отрезок вверх по оси O y. Таким образом, областью значений данной функции будет  .
.
б)Исследуем функцию на четность и нечетность. Найдем 
Таким образом, функция не является ни четной, ни нечетной и, значит, данная функция является функцией общего вида.
41-50. Найти пределы функций, не пользуясь правилом Лопиталя.
41. а) 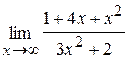 ; б)
; б)  .
.
42. а)  ; б)
; б)  .
.
43. а)  ; б)
; б) 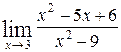 .
.
44. а)  ; б)
; б)  .
.
45. а)  ; б)
; б) 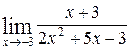 .
.
46. а) 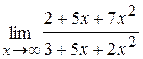 ; б)
; б)  .
.
47. а)  ; б)
; б) 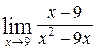 .
.
48. а)  ; б)
; б)  .
.
49. а) 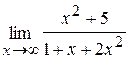 ; б)
; б)  .
.
50. а) 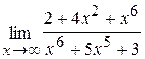 ; б)
; б)  .
.
|
|
|
|
|
Дата добавления: 2014-11-18; Просмотров: 344; Нарушение авторских прав?; Мы поможем в написании вашей работы!