
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Неопределённый и определённый интегралы
|
|
|
|
.
.
.
Пример..
95.. 100..
94.. 99..
93.. 98..
92.. 97..
91.. 96..
Исследование функций и построение графиков
91-100. Исследовать методами дифференциального исчисления функцию  и, используя результаты исследования, построить ее график.
и, используя результаты исследования, построить ее график.
1. Область определения:  .
.
2. 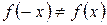 ,
, 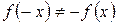 , -следовательно, функция не является четной, нечетной, периодической.
, -следовательно, функция не является четной, нечетной, периодической.
3. Исследуем характер точки разрыва  и поведение функции вблизи этой точки:
и поведение функции вблизи этой точки:
 ,
,
Таким образом, в точке  функция терпит разрыв второго рода, а прямая
функция терпит разрыв второго рода, а прямая  является вертикальной асимптотой.
является вертикальной асимптотой.
4. Определим уравнение наклонной асимптоты:
 , где
, где
 ,
,
Итак,
 -наклонная асимптота.
-наклонная асимптота.
5. Определим критические точки.
 ,
,
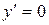 при
при  или
или 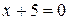 , то есть при
, то есть при  или
или  , - других критических точек в области определения функции нет. Значения функции в критических точках:
, - других критических точек в области определения функции нет. Значения функции в критических точках:
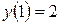 ,
,  .
.
6. Найдем вторую производную:
 , следовательно, точек перегиба нет.
, следовательно, точек перегиба нет.
7. Внесем все полученные данные в таблицу, определим поведение функции на различных участках и построим график.
| x | 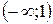
| 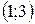
| 
| 
| |||

| + | - | - | + | |||
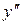
| - | - | - | + | + | + | |
    y y
| max | min |
Положительные значения первой производной соответствуют промежуткам возрастания, отрицательные – промежуткам убывания. Положительные значения второй производной соответствуют промежуткам вогнутости функции, отрицательные – промежуткам выпуклости. Точка, в которой возрастание функции сменяется убыванием, является точкой максимума, а точка, в которой убывание функции сменяется возрастанием – точкой минимума.

101-110. Найти неопределённые интегралы.
101. а). 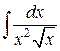 ; б).
; б). 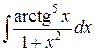 ; в).
; в).  .
.
102. а). 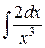 ; б)
; б) 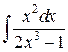 ; в).
; в). 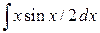 .
.
103. а).  ; б)
; б)  ; в).
; в).  .
.
104. а).  ; б)
; б)  ; в).
; в).  .
.
105. а).  ; б)
; б)  ; в).
; в).  .
.
106. а)  ; б)
; б)  ; в)
; в) 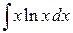 .
.
107. а)  ; б)
; б) 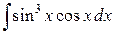 ; в)
; в) 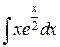 .
.
108. а)  ; б)
; б) 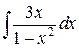 ; в)
; в)  .
.
109. а)  ; б)
; б)  ; в)
; в)  .
.
110. а)  ; б)
; б)  ; в)
; в) 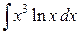 .
.
Пример. Найти неопределённые интегралы.
а)  ; б)
; б)  ; в)
; в) 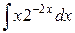 .
.
а) Данный интеграл не является табличным. Поэтому предварительно сделаем элементарные математические преобразования, в данном случае воспользовавшись формулой сокращенного умножения, а потом таблицей интегралов основных элементарных функций, получим:
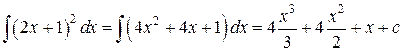
б) пусть требуется найти интеграл вида  , где подынтегральная функция непрерывна. Сделаем замену
, где подынтегральная функция непрерывна. Сделаем замену  , тогда
, тогда  . Получим
. Получим  . В найденном интеграле перейдем к прежней переменной
. В найденном интеграле перейдем к прежней переменной  , воспользовавшись равенством
, воспользовавшись равенством  .
.
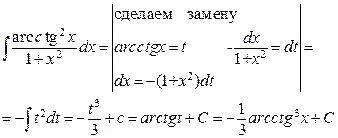 .
.
в) 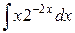 . Имеем интеграл вида
. Имеем интеграл вида  . Применим формулу интегрирования по частям
. Применим формулу интегрирования по частям  :
:
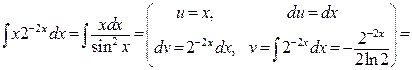
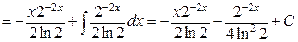 .
.
111-120. Вычислить определенные интегралы
111. а) 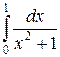 ; б)
; б) 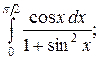 в)
в)  .
.
112. а)  ; б)
; б)  ; в)
; в)  .
.
113. а) 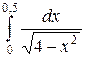 ; б)
; б) 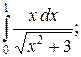 в)
в)  .
.
114. а) 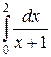 ; б)
; б)  в)
в)  .
.
115. а)  ; б)
; б)  в)
в) 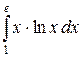 .
.
116. а)  ; б)
; б)  в)
в)  .
.
117. а)  ; б)
; б) 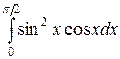 ; в)
; в)  .
.
118. а)  ; б)
; б)  в)
в)  .
.
119. а)  ; б)
; б)  в)
в) 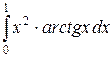 .
.
120. а)  ; б)
; б) 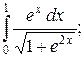 в)
в)  .
.
|
|
|
|
|
Дата добавления: 2014-11-18; Просмотров: 409; Нарушение авторских прав?; Мы поможем в написании вашей работы!