Пример. 2 страница

228. Закон распределения случайной величины имеет вид:

	-4	-1
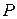
	0,2	0,1		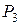0,2	0,1

Вычислить: , .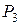

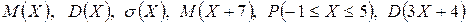229. Закон распределения случайной величины имеет вид:

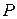
	0,2	0,3		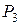0,1	0,05

Вычислить: , .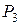

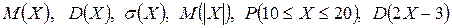230. Закон распределения случайной величины имеет вид:

	-100	-25
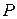
	0,3	0,1		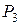0,1	0,3

Вычислить: , .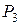

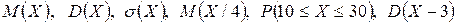Пример. Случайная величина имеет распределение:

	-30	-20
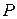
	0,2	0,3		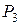0,1	0,2

Вычислить: , .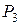

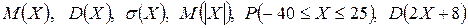Пусть закон распределения случайной величины представлен в виде

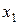
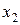
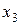
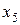
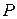
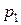
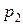
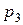
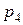
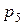
Т.к. закон распределения данной дискретной величины представляет полную группу событий, то сумма всех вероятностей равна 1.

.

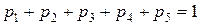Тогда искомая вероятность:

.

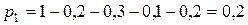Математическое ожидание случайной величины находится по формуле:

;

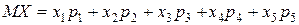в нашей задаче

.

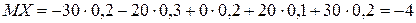Дисперсия случайной величины:

.

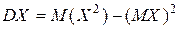Чтобы найти 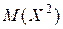, найдем закон распределения величины 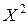. Для этого возведем все значения, которые принимает , в квадрат.

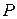
	0,2	0,3	0,2	0,1	0,2

Тогда

.

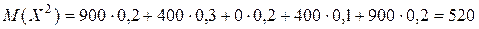Отсюда

.

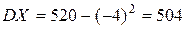Среднее квадратическое отклонение случайной величины:

;

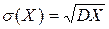тогда

.

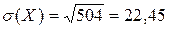Чтобы найти 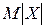, найдем распределение величины :

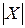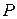
	0,2	0,3	0,2	0,1	0,2

Найдем :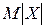

.

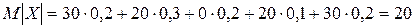Для нахождения 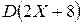следует знать соотношения:

;

.

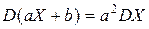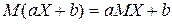Тогда для нашего примера

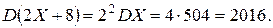
Чтобы найти 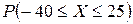, следует рассмотреть те значения , которые попадают в заданный интервал. Это значения 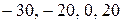. Этим значениям соответствуют вероятности 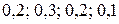. События, состоящие в том, что принимает данные значения, несовместны, следовательно, искомая вероятность 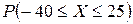равна сумме вероятностей:

.

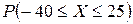
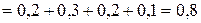231 - 240. Случайная величина задана функцией распределения F (x). Найти плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины.

231. 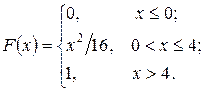232.

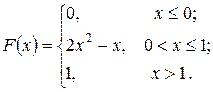
233. 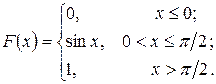234.

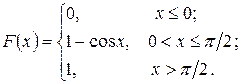
235. 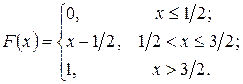236.

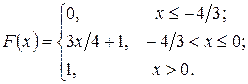
237. 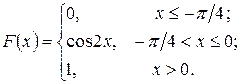238.

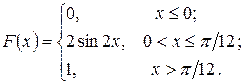
239. 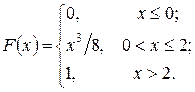240.

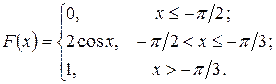
Пример. Случайная величина задана функцией распределения F (x). Найти плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины.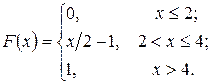

Найдем плотность распределения:

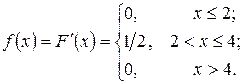
Используя определения математического ожидания и дисперсии для непрерывных случайных величин:

, ,

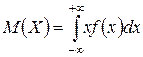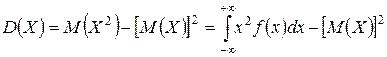получаем:

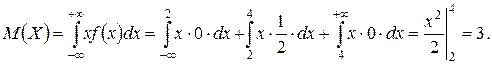
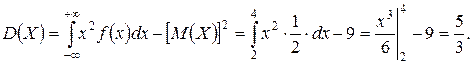
241. Плотность распределения случайной величины имеет вид:

.

Найти: , , .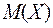

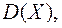
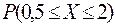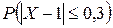242. Случайная величина имеет нормальное распределение с плотностью:

.

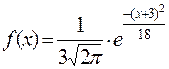Найти: , , .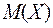

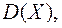
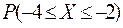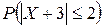243. Плотность распределения случайной величины имеет вид:

.

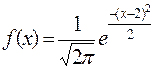Найти: , , .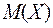

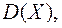
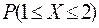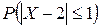244. Плотность распределения случайной величины имеет вид:

.

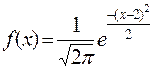Найти: , , .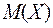

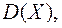
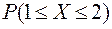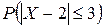245. Плотность распределения случайной величины имеет вид:

.

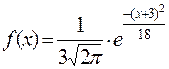Найти: , , .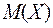

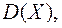
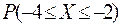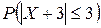246. Плотность распределения случайной величины имеет вид:

.

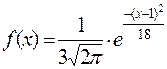Найти: , , .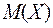

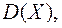
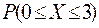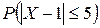247. Случайная величина 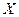имеет плотность распределения:

.

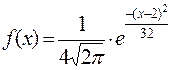Найти: , , .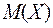

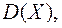
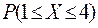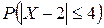248. Функция распределения случайной величины 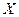имеет вид:

.

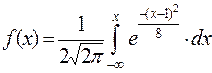Найти: , , .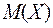

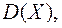
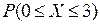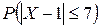249. Плотность распределения случайной величины имеет вид:

.

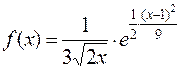Найти: , , .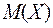

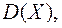
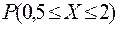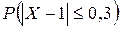250. Случайная величина имеет нормальное распределение с плотностью:

.

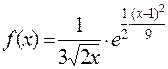Найти: , , .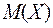

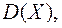
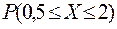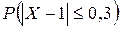Пример. Плотность распределения случайной величины имеет вид:

.

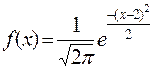Найти: , , , .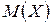

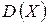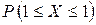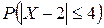Нормально распределенная случайная величина имеет плотность распределения:

,

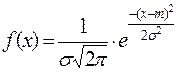где математическое ожидание 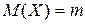, дисперсия .

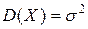В нашем примере ; .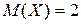

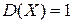Для нормальной случайной величины вероятность 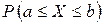равна:

.

.

;

.

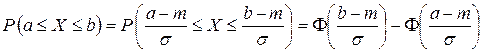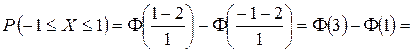
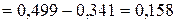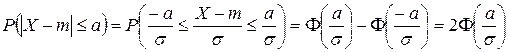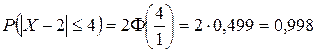251-260. Из партии в 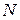образцов бетона путем бесповторной выборки отобрано 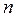образцов. Измерения прочности отобранных деталей дали выборочное среднее 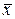МПа и выборочное среднее квадратическое отклонение 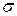МПа. Некондиционными признано 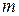образцов. С вероятностью 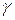найти:

1.Доверительный интервал для генеральной средней .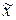

2.Доверительный интервал для генеральной доли некондиционных изделий .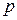

01.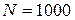
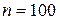
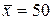
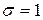
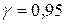
02.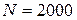
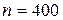
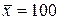
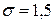
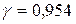
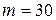
03.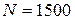
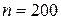
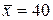
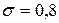
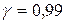
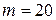
04.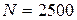
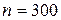
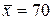
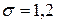
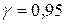
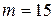
05.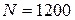
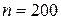
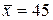
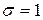
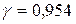
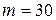
06.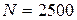
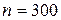
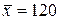
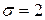
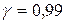
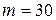
07.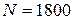
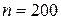
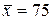
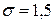
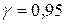
08.
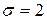
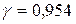
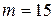
09.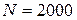
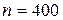
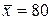
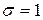
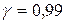
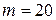
110.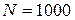

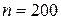
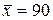
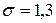
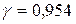
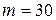
Пример. Из 1000 образцов бетона для контроля прочности бесповторным путем отобрали 200 образцов. Изучение выборочной совокупности дало величину выборочной средней 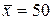МПа и выборочное среднее квадратическое отклонение 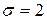МПа. Двадцать образцов признано некондиционными (не соответствующими стандартам качества).

Найти:

а) с вероятностью 0,95 доверительный интервал для генеральной средней;

б) с вероятностью 0,954 долю некондиционных изделий в генеральной совокупности.

а) По условию, , .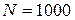

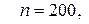
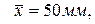
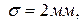
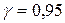Доверительный интервал для генеральной средней имеет границы:

,

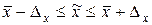где 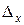- предельная ошибка для бесповторной выборки

.

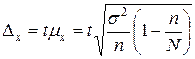Параметр 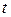определяется из равенства 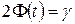, или 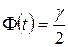. По таблице функции Лапласа находят аргумент 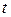, которому соответствует значение функции Лапласа, равное .

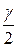В нашем примере .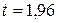

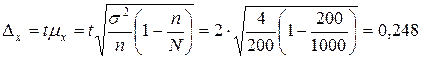(МПа).

Тогда доверительный интервал для нашего примера:

;

.

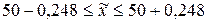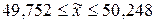С вероятностью 0,95 (в строительстве применяют термин надежность) генеральная средняя прочности бетона находится от 49,752 МПа до 50,248 МПа, т.е. с надежностью 0,95 прочность образцов лежит в найденном интервале. На практике при вычислении доверительного интервала для прочности используется нижняя граница интервала, т.к. нас интересует большая прочность. Тогда прочность образцов будет больше, чем 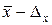, с вероятностью .

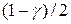В нашей задаче прочность будет больше, чем 49,752, с вероятностью 0,025.

б) .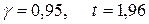

Выборочная доля некондиционных изделий

.

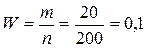Предельная ошибка для генеральной доли

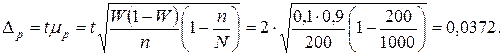
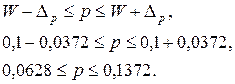
С вероятностью 0,95 доля некондиционных изделий во всей партии составляет от 6,28% до 13,72%.

261-270. С целью изучения статистического признака Х проведено исследование. Результаты представлены в таблице. Определить:

1) среднее значение признака Х;

2) дисперсию, среднее квадратическое отклонение;

3) коэффициент вариации;

4) моду признака Х (аналитически и графически);

5) медиану признака Х (аналитически и графически).

261. Распределение рабочих цеха по возрасту.

Возраст (X), годы	17 - 20	20 - 30	30 - 40	40 - 50	50 - 59	всего
Количество рабочих

262. Распределение рабочих по стажу работы.

Дата добавления: 2014-11-18