
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример. 1 страница
|
|
|
|
Задание 1.1. Бросают три игральные кости. Найти вероятность того, что на верхних гранях появится число очков, сумма которых делится на 5.
Определим испытание и его результат, т.е. элементарное событие. Испытанием бросание трех игральных костей, результатом – одно из сочетаний очков на верхних гранях трех костей. Исследуемое событие А – сумма очков на трех верхних гранях делится на 5. Вероятность события А находится по формуле:  .
.
Общее количество элементарных событий n можно найти по правилу умножения. На каждой игральной кости 6 граней, и все они могут сочетаться со всеми гранями других костей. Итак, получаем:
 .
.
Количество элементарных событий m, входящих в состав события А, или благоприятствующих событию А, найдем, выписав все возможные результаты испытаний, и оставив из них только те, для которых сумма очков на всех трех костях делится на 5. Имеем:
В результате получим, что m= 43. Следовательно, искомая вероятность:
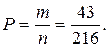
Задание 1.2. Слово «МАТЕМАТИКА» составлено из карточек, на каждой из которых написана только одна буква. Затем карточки перемешивают и вынимают без возврата по одной. Найти вероятность случая, что буквы появятся в порядке заданного слова.
Испытание заключается в вынимании карточек с буквами в случайном порядке без возврата. Элементарным событием является полученная последовательность букв. Событие А состоит в получении нужного слова «МАТЕМАТИКА». Так как элементарные события являются перестановками из 10 букв, то 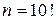 Некоторые буквы в слове «МАТЕМАТИКА» повторяются (М – 2 раза, А – 3 раза, Т – 2 раза). Поэтому возможны перестановки, при которых слово не меняется. Их число равно:
Некоторые буквы в слове «МАТЕМАТИКА» повторяются (М – 2 раза, А – 3 раза, Т – 2 раза). Поэтому возможны перестановки, при которых слово не меняется. Их число равно:  =24.
=24.
Таким образом,  .
.
Задание 1.3. (решается аналогично задаче 1.2).
Задание 1.4. В урне 5 черных и 6 белых шаров. Случайным образом вынимают 4 шара. Найти вероятность того, что среди них имеется:
а) 2 белых шара;
б) меньше, чем 2 белых шара;
в) хотя бы один белый шар.
Испытанием будет случайное вынимание 4 шаров. Элементарными событиями являются всевозможные сочетания по 4 из 11 шаров. Их число равно:
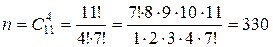 .
.
а)  - среди вынутых шаров 2 белых. Значит, среди вынутых шаров – 2 белых и 2 черных (т.к. вынимают 4). Используя правило умножения, получаем:
- среди вынутых шаров 2 белых. Значит, среди вынутых шаров – 2 белых и 2 черных (т.к. вынимают 4). Используя правило умножения, получаем:
 ,
, 
б) 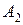 - среди вынутых шаров меньше, чем 2 белых. Это событие состоит из двух несовместных событий:
- среди вынутых шаров меньше, чем 2 белых. Это событие состоит из двух несовместных событий:
В 1 – среди вынутых шаров 1 белый и 3 черных шара;
В 2 - все вынутые шары – черные.
Следовательно,  .
.
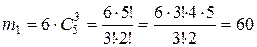 ,
,  .
.
 ;
; 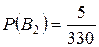 ;
; 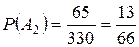 .
.
в)  - среди вынутых шаров хотя бы один белый. Этому событию удовлетворяют следующие сочетания шаров:
- среди вынутых шаров хотя бы один белый. Этому событию удовлетворяют следующие сочетания шаров:
В 1 – среди вынутых шаров 1 белый и 3 черных шара;
В 2 - среди вынутых шаров 2 белый и 2 черных шара;
В 3 - среди вынутых шаров 3 белых и 1 черный шар;
В 4 - среди вынутых шаров 4 белых шара.
Прямое решение этой задачи приводит обычно к сложным вычислениям. Проще сначала найти вероятность противоположного события, а затем вычислить вероятность искомого.
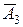 - среди вынутых шаров нет ни одного белого. В этом случае
- среди вынутых шаров нет ни одного белого. В этом случае
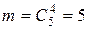 ;
; 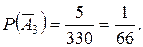
Тогда 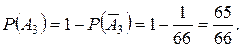
Ответ:  ;
;  ;
; 
Задание 1.5. Устройство состоит из трех независимых элементов, работающих в течение времени Т безотказно соответственно с вероятностями 0,851, 0,751, 0,701. Найти вероятность того, что за время Т выйдет из строя:
а) только один элемент;
б) хотя бы один элемент.
Испытание, т.е. работу за время Т, нужно рассмотреть на двух уровнях: на уровне устройства и на уровне элементов. Элементарные события определять не надо, так как их вероятности заданы.
а)  - за время Т выходит из строя только один элемент:
- за время Т выходит из строя только один элемент:
 - первый элемент выходит из строя;
- первый элемент выходит из строя;
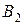 - второй элемент выходит из строя;
- второй элемент выходит из строя;
 - третий элемент выходит из строя;
- третий элемент выходит из строя;
 - первый элемент не выходит из строя;
- первый элемент не выходит из строя;
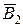 - второй элемент не выходит из строя;
- второй элемент не выходит из строя;
 - третий элемент не выходит из строя.
- третий элемент не выходит из строя.
Учитывая независимость элементов устройств, несовместность событий  и
и  , получаем следующую формулу:
, получаем следующую формулу:
 .
.
По условию,
 = 0,851,
= 0,851, 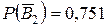 ,
,  0,701.
0,701.
Тогда
 ,
, 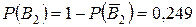 ,
,
 .
.
Следовательно, получаем:
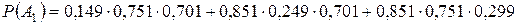 =0,418.
=0,418.
б) 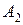 - за время Т выходит из строя хотя бы один элемент.
- за время Т выходит из строя хотя бы один элемент.
Так как событие определяется словами «хотя бы один», используем противоположное событие:
 - за время Т все элементы работают безотказно.
- за время Т все элементы работают безотказно.
 .
.
Ответ:  ,
,  .
.
Задание 1.6. В первой урне 6 белых и 4 черных шара, а во второй 5 белых и 7 черных шаров. Из первой урны взяли 3 шара наугад, а из второй – 2 шара. Найти вероятность того, что среди вынутых шаров:
а) все шары одного цвета;
б) только 3 белых шара;
в) хотя бы один белый шар.
Шары вынимали из обеих урн независимо. Испытаниями являются извлечение трех шаров из первой урны и двух шаров из второй. Элементарными событиями будут сочетания по 3 или 2 из 10 или 12 шаров соответственно.
а)  - все вынутые шары одного цвета, т.е. они или все белые, или все черные. Определим для каждой урны все возможные события:
- все вынутые шары одного цвета, т.е. они или все белые, или все черные. Определим для каждой урны все возможные события:
 - из первой урны вынуты 3 белых шара;
- из первой урны вынуты 3 белых шара;
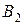 - из первой урны вынуты 2 белых шара и 1 черный шар;
- из первой урны вынуты 2 белых шара и 1 черный шар;
 - из первой урны вынуты 1 белый шар и 2 черных шара;
- из первой урны вынуты 1 белый шар и 2 черных шара;
 - из первой урны вынуты 3 черных шара;
- из первой урны вынуты 3 черных шара;
 - из второй урны вынуты 2 белых шара;
- из второй урны вынуты 2 белых шара;
 - из второй урны вынуты 1 белый и 1 черный шар;
- из второй урны вынуты 1 белый и 1 черный шар;
 - из второй урны вынуты 2 черных шара.
- из второй урны вынуты 2 черных шара.
Таким образом,
 .
.
Найдем количество элементарных событий 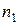 и
и  для первой и второй урн соответственно. Имеем:
для первой и второй урн соответственно. Имеем:
 ,
,  .
.
Найдем количество каждого из элементарных событий, определяющих следующие события:
 :
:  ,
,  :
:  ,
,
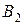 :
:  ,
,  :
:  ,
,
 :
:  ,
,  :
:  ,
,
 :
: 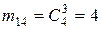 .
.
Следовательно,
 .
.
б) 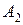 - среди извлеченных шаров только 3 белых. В этом случае:
- среди извлеченных шаров только 3 белых. В этом случае:
 .
.
в)  - среди извлеченных шаров имеется по крайней мере один белый.
- среди извлеченных шаров имеется по крайней мере один белый.
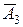 - среди извлеченных шаров нет ни одного белого шара.
- среди извлеченных шаров нет ни одного белого шара.
Тогда: 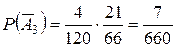 ,
,  .
.
Ответ: 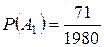 ,
,  ,
,  .
.
201. В банк поступило 6 заявлений от физических лиц на получение кредита. Вероятность получить первый кредит для каждого одинакова. Найти вероятности следующих событий:
а) будет выдано ровно 3 кредита;
б) будет выдано не менее двух кредитов.
202. Доля крупных заказов в строительной фирме составляет 40%. Фирма в месяц заключает в среднем 7 заказов.
Найти вероятности следующих событий:
а) фирме будет сделано 2 крупных заказа;
б) будет сделано не менее четырех крупных заказов.
203. В банк поступило 10 стодолларовых купюр. Какова вероятность того, что среди них окажется
а) 5 фальшивых купюр,
б) менее 5 фальшивых купюр, если известно, что на рынке 0,1% купюр фальшивых?
204. Коммерческий банк имеет 6 отделений, каждое из которых заказывает независимо друг от друга крупную сумму денег на следующий рабочий день с вероятностью 0,1. Какова вероятность того, что заявок на крупную сумму будет:
а) две;
б) не менее четырех.
205. Вероятность обращения клиента в банк за возвращением депозита 0,4. Найти вероятность того, что из 7 вип-клиентов банка за возвращением депозита обратится:
а) один клиент;
б) все клиенты.
206. Провайдер обслуживает 10 абонентов сети INTERNET. Вероятность того, что любой абонент захочет войти в сеть в течение часа, равна 0.002. Найти вероятность того, что в течение часа
а) более 7 абонентов попытаются войти в сеть,
б) не менее 7 абонентов попытаются войти в сеть.
207. В банк поступило 8 заявлений от юридических лиц на получение кредита. Вероятность получить кредит для каждого одинакова и равна 0,55. Найти вероятности следующих событий:
а) будет выдано ровно 2 кредита;
б) будет выдано не менее пяти кредитов.
208. Доля крупных заказов в строительной фирме составляет 72%. Фирма в месяц заключает в среднем 4 заказа. Найти вероятности следующих событий:
а) фирме будет сделано 2 крупных заказа;
б) будет сделано не менее двух крупных заказов.
209. Вероятность того, что кредит не вернут в банк, составляет 0,1. Найти вероятность того, что из 8 клиентов, получивших кредит, его не вернут:
а) один клиент;
б) все клиенты.
210. Фирма – импортер поставляет продукцию на 7 крупных предприятий города. Вероятность того, что этими предприятиями будет сделан заказ в отчетного периода, составляет 12%. Найти вероятность того, что в течение отчетного периода заказ будет сделан
а) более чем 6 предприятиями,
б) не будет сделан вообще.
Пример. Вероятность обращения владельцев транспортных средств в страховую компанию за возмещением составляет 0,8. Найти вероятность того, что из10 автовладельцев 9 обратятся в страховую компанию.
Решение.
Используем формулу Бернулли, которая принадлежит к схеме независимых повторных испытаний.
Проводится n независимых друг от друга испытаний, в каждом из которых событие А может появиться с одной и той же вероятностью  . Обозначим
. Обозначим  - вероятность того, что в n испытаниях событие А появится ровно k раз. Иногда говорят, что
- вероятность того, что в n испытаниях событие А появится ровно k раз. Иногда говорят, что  - вероятность того, что в n испытаниях было
- вероятность того, что в n испытаниях было 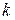 успехов. Тогда
успехов. Тогда
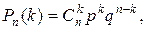

 .
.
Количество испытаний в данной задаче n = 10. Вероятность того, что будет предъявлен иск в страховую компанию  ;
; 
Найдем вероятность, что будет предъявлено 9 исков из 10, т.е. число успехов равно 9.

211. Курс доллара повышается в течение квартала с вероятностью 0,8 и понижается с вероятностью 0,2. При повышении курса доллара фирма рассчитывает получить прибыль с вероятностью 0,85; при понижении — с вероятностью 0,5. Найти вероятность того, что
а) фирма получит прибыль;
б) фирма получит прибыль, при этом известно, что курс доллара понизится.
212. В страховой компании 500 начинающих и 2000 опытных водителей. В среднем 10 % начинающих и 2 % опытных водителей в течение года попадают в аварию. Найти вероятность того, что
а) водитель попал в аварию;
б) это был опытный водитель.
213. Вероятность того, что клиент банка не вернет кредит в период экономического роста, равна 0,04, а в период экономического кризиса – 0,13. Вероятность того, что начнется период экономического роста, равна 0,65. Чему равна вероятность того, что
а)случайно выбранный клиент банка не вернет полученный кредит;
б) случайно выбранный клиент банка не вернет полученный кредит в период экономического роста.
214. Курортная гостиница будет заполнена в июле с вероятностью 0.92, если будет солнечная погода, или с вероятностью 0.72, если будет дождливая погода. По оценкам синоптиков в данной местности в июле бывает 75% солнечных дней. Какова вероятность того, что
а) работа гостиницы будет рентабельной;
б) работа гостиницы будет рентабельной, если погода будет дождливой.
215. Вероятность того, что новый товар будет пользоваться спросом на рынке, если конкурент не выпустит в продажу аналогичный товар, равна 0,67, а при наличии на рынке конкурирующего товара, равна 0,42. Вероятность того, что конкурирующая фирма выпустит на рынок аналогичный товар в течение интересующего нас периода, равна 0,35. Чему равна вероятность того, что
а) новый товар будет иметь успех;
б) новый товар будет иметь успех при наличии на рынке конкурирующего товара
216. Экономист-аналитик условно подразделяет экономическую ситуацию в стране на «хорошую», «посредственную» и «плохую» и оценивает их вероятности для данного момента времени в 0,15; 0,70 и 0,15 соответственно. Некоторый индекс экономического состояния возрастает с вероятностью 0,60, когда ситуация «хорошая»; с вероятностью 0,30, когда ситуация посредственная, и с вероятностью 0,10, когда ситуация «плохая». Чему равна вероятность того, что
а) экономика страны на подъеме;
б) экономика страны на подъеме при росте индекса экономического состояния.
217. Три организации представили в контрольное управление счета для выборочной проверки. Первая организация представила 15 счетов, вторая — 10, третья — 25. Вероятности правильного оформления счетов у этих организаций известны и соответственно равны: 0,9; 0,8; 0,85. Был выбран один счет и он оказался правильным. Определить вероятность того, что этот счет принадлежит второй организации.
218. Инвестор приобрел акции трех компаний, причем его инвестиционный пакет состоит из 20 акций первой компании, 42 акций второй и 18 акций третьей. Вероятность того, что акции первой компании принесут прибыль, равна 0,5, второй -0,3, третьей- 0,7. Найти вероятность того, что
а) инвестор получит прибыль;
б) инвестор получит прибыль, если прогнозирует рост цен акций первой компании.
219. Курс гривны понижается в течение недели с вероятностью 0,6 и повышается с вероятностью 0,4. При повышении курса гривны фирма рассчитывает получить прибыль с вероятностью 0,45; при понижении — с вероятностью 0,2. Найти вероятность того, что
а) фирма получит прибыль;
б) фирма получит прибыль, при этом известно, что курс гривны понизится.
220. Количество акций, представленных тремя различными предприятиями на финансовый рынок, относятся как 5:3:2. Вероятности того, что акции будут котироваться по 12 долл. за штуку для этих предприятий соответственно равны 0,3; 0,4; 0,7. Известно, что цена случайно выбранной акции составила 12 долл. Найти вероятность того, что эта акция представлена третьим предприятием.
Пример. Фирма – экспортер промышленной продукции собирается заключить контракт с крупным концерном на его поставку. Если основной конкурент фирмы не станет одновременно претендовать на заключение контракта, то вероятность подписания контракта оценивается аналитиками фирмы в 0,55, в противном случае – в 0,35. По оценкам аналитиков вероятность того, что конкурент выдвинет свои предложения по заключению контракта, равна 0,4. Чему равна вероятность заключения контракта для фирмы – экспортера. И какова будет эта вероятность, если фирма – конкурент все таки выдвинет свои предложения.
Решение.
Пусть А – событие «фирма – экспортер заключит контракт»; H1 – гипотеза «фирма-конкурент выдвинет свои предложения», H2 – гипотеза «фирма-конкурент не выдвинет свои предложения». По условию,

условные вероятности по заключению контракта для фирмы-экспортера  По формуле полной вероятности вероятность заключения контракта для фирмы – экспортера будет равна:
По формуле полной вероятности вероятность заключения контракта для фирмы – экспортера будет равна:

А вероятность того, что контракт будет заключен, если фирма – конкурент все таки выдвинет свои предложения найдем по формуле Байеса:
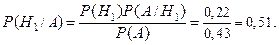
221. Закон распределения случайной величины  имеет вид:
имеет вид:

| -8 | -4 | -2 | |
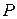
| 0,3 | 
| 0,2 | 0,1 |
Вычислить:  ,
,  .
.
222. Закон распределения случайной величины  имеет вид:
имеет вид:

| -5 | |||
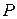
| 
| 0,2 | 0,1 | 0,3 |
Вычислить:  ,
, 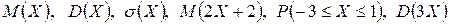 .
.
223. Закон распределения случайной величины  имеет вид:
имеет вид:

| -5 | -3 | -1 | ||
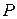
| 
| 0,1 | 0,2 | 0,3 | 0,2 |
Вычислить:  ,
,  .
.
224. Закон распределения случайной величины  имеет вид:
имеет вид:

| -4 | -1 | |||
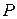
| 0,3 | 0,1 | 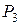
| 0,1 | 0,3 |
Вычислить: 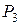 ,
,  .
.
225. Закон распределения случайной величины  имеет вид:
имеет вид:

| ||||
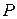
| 0,3 | 0,2 | 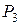
| 0,2 |
Вычислить: 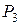 ,
,  .
.
226. Закон распределения случайной величины  имеет вид:
имеет вид:

| |||||
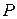
| 0,1 | 0,36 | 0,35 | 0,14 | 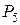
|
Вычислить: 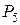 ,
,  .
.
227. Закон распределения случайной величины  имеет вид:
имеет вид:

| ||||
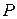
| 0,3 | 0,2 | 0,1 | 
|
Вычислить:  ,
,  .
.
|
|
|
|
|
Дата добавления: 2014-11-18; Просмотров: 4407; Нарушение авторских прав?; Мы поможем в написании вашей работы!