
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Коэффициенты несимметричности нагрева
|
|
|
|
| Схема нагрева | Расположение заготовок по отношению к тепловому потоку | Коэффициент несимметричности 
| ||||||||||
 1 1 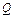
                         
| Односторонний нагрев на монолитном поду | 1,0 | ||||||||||
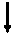 2 2 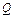
| Двусторонний нагрев на глиссажных трубах | 0,55 | ||||||||||
  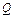 h h
| Односторонний нагрев на монолитном поду(с зазором между заготовками) |
| ||||||||||
   4 4
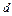
| Односторонний нагрев на монолитном поду | 0,75 – 0,8 | ||||||||||
    5 5  
                           
| Односторонний нагрев на монолитном поду |
| ||||||||||
        6 dэкв 6 dэкв
  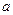
 
|
Четырёхсторонний нагрев плоской
заготовки  ; ; 
|

| ||||||||||
    7 b 7 b
  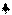   
| Четырёхсторонний нагрев плоской заготовки

|

| ||||||||||
    8 8
 d d
| Круглые вертикальные заготовки | 0,5 |
Для насыпных загрузок, состоящих из нескольких слоев деталей, когда размеры отдельных деталей невелики относительно размера всей загрузки, теплофизические свойства загрузки как целого можно рассматривать как "эффективные". Величина эффективной теплопроводности зависит от температуры, свойств материала деталей, формы полостей между ними. Эффективная теплопроводность некоторых промышленных загрузок представлена в табл.8.
На кафедре технологии материалов Волгоградского государственного технического университета доцентом Б.З. Кононовым на основании обработки результатов экспериментов по измерению теплопроводности сложных загрузок (слоистых: листы, сложенные в пачку, лента, свёрнутая в рулон; волокнистых: с вязки прутков, бунты проволоки, намотка проволоки на шпуле и зернистых: слой болтов или гаек в поддоне или на конвейерной ленте, слой мелких поковок или отливок на поддоне) было получено уравнение для расчёта эквивалентного теплопроводности сложной загрузки по формуле (43)
 , (37)
, (37)
где  температура загрузки,
температура загрузки, 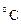 ;
;
 приведённый диаметр или относительная крупность элементов загрузки, то есть отношение характерного размера элемента к толщи не нагреваемого слоя загрузки;
приведённый диаметр или относительная крупность элементов загрузки, то есть отношение характерного размера элемента к толщи не нагреваемого слоя загрузки;
 коэффициент формы элемента загрузки.
коэффициент формы элемента загрузки.
Анализ уравнения (37) подтверждает, что наибольшее тепловое сопротивление – у слоистой загрузки, среднее положение занимает волокнистая, а наименьшее тепловое сопротивление имеет зернистая загрузка.
Насыпная плотность – это величина, появляющаяся в тех случаях, когда изделия загружены для нагрева плотным толстым слоем, то есть мелкие изделия уложены беспорядочно (насыпаны) и слой загрузки в 2–3 раза больше среднего размера изделия. Чаще всего такой способ применяется для нормализации мелких поковок или отливок на поддонах.
В этом случае рассчитывают процесс нагрева не отдельного единичного изделия, а всего слоя загрузки в целом. Поэтому в расчете используется приведенный коэффициент теплопроводности  и насыпная плотность слоя загрузки
и насыпная плотность слоя загрузки  , которая может быть представлена
, которая может быть представлена
 , (38)
, (38)
где  – коэффициент заполнения, т.е. объёмная доля пространства слоя, занимаемая непосредственно материалом;
– коэффициент заполнения, т.е. объёмная доля пространства слоя, занимаемая непосредственно материалом;
 плотность материала, кг/м3.
плотность материала, кг/м3.
Иногда применяют термин – коэффициент порозности  , т.е. объёмная доля пустот (
, т.е. объёмная доля пустот ( . Выбор коэффициента заполнения (или порозности) следует производить на основе производственного опыта.
. Выбор коэффициента заполнения (или порозности) следует производить на основе производственного опыта.
Таблица 8
|
|
|
|
|
Дата добавления: 2014-11-18; Просмотров: 1926; Нарушение авторских прав?; Мы поможем в написании вашей работы!




