Зв’язок між числом дійсних знаків і похибкою числа

Абсолютна похибка наближеного числа a зв’язана з числом дійсних знаків співвідношенням:

, (1.16)

що слідує з означення дійсної значущої цифри. Запишемо наближене число:

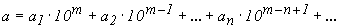, (1.17)

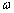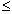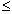де , всі цифри якого при даному виборі параметра дійсні (0,5 w 1).

Розділивши дві частини нерівності (1.16) на 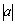, отримаємо:

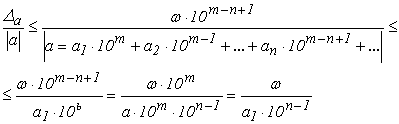(1.18)

тобто

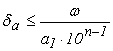, (1.19)

n – кількість дійсних значущих цифр.

За граничну відносну похибку можна прийняти.

(1.20)

Приклад 1. Яка гранична відносна похибка наближеного числа a=4,176 якщо воно має тільки вірні цифри у вузькому змісті?

Розв‘язок. Так як в числі 4,176 усі чотири цифри вірні у вузькому змісті, то вибираємо 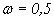. По формулі (1.20) знаходимо граничну відносну похибку.

.

Зауважимо, що граничну відносну похибку числа a можна знайти, використовуючи формулу . Так як в даному числі а всі цифри вірні у вузькому змісті, то . Тоді

.

Як бачимо, різниця невелика, але застосування формули (1.20) трохи спрощує обчислення .

Приклад 2. Яка гранична відносна похибка числа a=14,278 якщо воно має тільки вірні цифри в широкому змісті?

.

Розв‘язок. Тому що всі п'ять цифр числа вірні в широкому змісті, те .

Приклад 3. Зі скількома вірними десятковими знаками у вузькому змісті потрібно взяти, щоб похибка не перевищувала 0,1%?

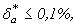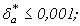
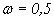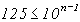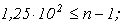
Розв‘язок. Тут тобто маємо звідки ; ; 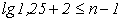, тобто 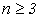, де n – найменший цілочисловий аргумент. Для більшої точності можна прийняти n=4.

Дата добавления: 2014-11-08