
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Обчислювальний експеримент та його основні етапи. Поняття стійкості та коректності
|
|
|
|
Звичайно метод математичного моделювання це ефективний засіб дослідження реальних інженерних об‘єктів та явищ. Але з їх ускладненням математичні моделі стають більш складними і їх дослідження вимагають величезної обчислювальної роботи. Застосування ЕОМ для розв‘язання складних прикладних задач сформувало новий спосіб проведення теоретичних досліджень на базі математичних моделей – обчислювальний (або математичний) експеримент..
В виділяють сім етапів обчислювального експерименту:
1. постановка задачі на дослідження,
2. побудова математичної моделі,
3. вибір чисельного методу розв‘язання математичної моделі,
4. розробка алгоритмів та програм,
5. тестування розроблених ПЗ на відомих моделях,
6. дослідження об‘єкта, який розглядається на ЕОМ,
7. аналіз результатів дослідження і застосування.
На першому та другому етапах вивчають суть явища або об‘єкта, що досліджується, з‘ясовують їх склад, закономірності і взаємозв‘язки окремих частин. Виділяють у явищі або об‘єкті дослідження основні і другорядні фактори. Основні фактори і закономірності досліджуваного явища записують у вигляді математичних формул. Це один з найскладніших етапів обчислювального експерименту. Складність полягає в тому, що він вимагає поєднання математичних і спеціальних знань. Тому над створенням математичної моделі працюють спільно математики і спеціалісти тієї галузі, до якої належить об‘єкт або явище, що досліджується.
Третій етап обчислювального експерименту пов‘язаний з вибором методу розв‘язування математичної моделі. Як правило, прикладні задачі описуються моделями, розв‘язання яких не можна знайти у вигляді аналітичних формул. Тоді з відомих чисельних методів підбирають найбільш ефективний. Для дослідження моделі на ЕОМ розробляють алгоритм. Слід пам‘ятати, що для однієї математичної задачі можна скласти, як правило, декілька алгоритмів. Визначення критеріїв для оцінки якості обчислювальних алгоритмів є предметом теорії чисельних методів. Основна її мета – побудова ефективних чисельних методів, які давали б можливість знаходити розв'язок поставленої математичної задачі з наперед заданою точністю з якомога меншими затратами машинного часу. Оцінюючи ефективність чисельного методу, враховують такі його характеристики, як універсальність, простоту організації обчислювального процесу і контролю його точності, швидкість збіжності, стійкість обчислювального процесу.
На четвертому етапі обчислювального експерименту вибирають середовище дослідження та розробляють алгоритми та програми для реалізації на ЕОМ.
П‘ятий та шостий етапи обчислювального експерименту полягають в дослідженні на ЕОМ. Спочатку проводять тестові розрахунки, які потрібні для налагодження програми і перевірки її відповідності реальному процесу математичної моделі. Для тестової задачі підбирають такі значення вхідних даних, щоб можна було оцінити достовірність розв'язку. Зіставлення знайденого за допомогою ЕОМ розв'язку з контрольним дає можливість уточнити математичну модель, або переконатися в тому, що вона добре описує досліджуваний об'єкт чи явище. Після цього проводять дослідження за розробленою програмою, яка виконується зазвичай в діалоговому режимі з ЕОМ. На цьому етапі обчислювального експерименту за допомогою математичної моделі передбачується поведінка досліджуваного об'єкта або явища в умовах, де реальні експерименти ще не проводились або зовсім неможливі.
Після проведення розрахунків на ЕОМ виконують сьомий етап обчислювального експерименту — всебічний аналіз результатів обчислень, на основі якого роблять висновки. Якщо результати надійні, то їх передають замовнику для подальшого використання; якщо результати розрахунків викликають сумнів щодо їх достовірності, тоді математичну модель модифікують, як правило, ускладнюють, і починається новий цикл обчислювального експерименту.
При виконанні всіх етапів обчислювального експерименту слід враховувати похибки вхідних даних задачі, що досліджується, які не можливо змінити в процесі дослідження, але необхідно знати, як вони впливають на точність кінцевого результату. Одні задачі мають похибку результату такого самого порядку, як і порядок похибки вхідних даних, в інших задачах похибка результату може на кілька порядків перевищувати похибку вхідних даних. Чутливість математичної моделі до неточностей у вхідних даних характеризується поняттям стійкості.
Задача називається стійкою за вхідними даними, якщо її розв'язок неперервний і залежить від вхідних даних, тобто малому приросту 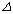 х вхідної величини відповідає малий приріст
х вхідної величини відповідає малий приріст 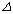 у шуканого розв'язку. Іншими словами, малі похибки вхідних даних спричинюють малі похибки розв'язку задачі. Якщо ця умова не виконується, то задача вважається нестійкою за вхідними даними. Це означає, що навіть незначні похибки вхідних даних можуть привести до як завгодно великих похибок розв'язку, тобто розв'язок може бути зовсім спотворений. Тому застосовувати безпосередньо до таких задач чисельні методи не можна, оскільки похибки округлень при застосуванні методу будуть катастрофічно нагромаджуватись у ході обчислень.
у шуканого розв'язку. Іншими словами, малі похибки вхідних даних спричинюють малі похибки розв'язку задачі. Якщо ця умова не виконується, то задача вважається нестійкою за вхідними даними. Це означає, що навіть незначні похибки вхідних даних можуть привести до як завгодно великих похибок розв'язку, тобто розв'язок може бути зовсім спотворений. Тому застосовувати безпосередньо до таких задач чисельні методи не можна, оскільки похибки округлень при застосуванні методу будуть катастрофічно нагромаджуватись у ході обчислень.
Розглянемо поняття коректності задачі. Задача називається коректно поставленою, якщо для будь-яких вхідних даних існує єдиний і стійкий за вхідними даними її розв'язок. Прикладом некоректно поставленої задачі є, задача чисельного диференціювання функцій.
Для розв'язування некоректно поставлених задач застосовувати класичні чисельні методи не варто, оскільки похибки округлень при розрахунках можуть катастрофічно зростати і призвести до результату, далекого від шуканого розв'язку. Для розв'язування некоректно поставлених задач використовують так звані методи регулярізації, які замінюють дану задачу коректно поставленою.
При аналізі результатівобчислювального експерименту (будь-якого моделювання математичного чи імітаційного) вирішується дві задачі теорії похибок пряма та зворотна.
Пряма задача – це визначення похибки результату рішення задачі на ЕОМ, що визначається неусувною похибкою, і вибір відповідного методу обчислень, допустимої похибки.
Зворотна задача – по доступній похибці результату визначаються похибки з якими можливе використання вхідних даних і постановки задачі.
|
|
|
|
|
Дата добавления: 2014-11-08; Просмотров: 1859; Нарушение авторских прав?; Мы поможем в написании вашей работы!