Модифікації методу Ейлера

З метою підвищення точності методу Ейлера використовують різні його модифікації.

Суть удосконаленого методу Ейлера полягає в використанні ітераційної формули виду:

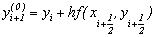, (9.16)

де - значення аргументу х в точці 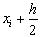, а - значення функції в точці .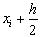

Розглянемо диференціальне рівняння

(9.17)

з початковою умовою .

Потрібно знайти розв’язок рівняння (9.13) на відрізку .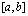

Розіб'ємо відрізок 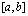на n рівних частин точками , де 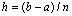– крок інтегрування

Алгоритм методу складається з:

1. визначення похідної 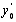в точці :

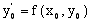
2. змінна х за формулою:

3. визначення значення при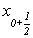

4. визначення похідної в точці (, )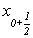

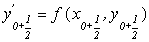
5. використовуємо отримане значення для визначення 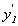за формулою:

,

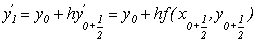6. змінюємо

7. повторюємо всі кроки алгоритму, починаючи з першого.

Графічна інтерпретація методу представлена на рисунку 9.7.

Рисунок 9.7 – Графічна інтерпретація удосконаленого методу Ейлера

Зауваження. Оцінка похибки в точці x_і може бути отримана за допомогою "подвійного прорахунку": розрахунок повторюють із кроком h/2 похибка більш точного значення (при кроці h/2) оцінюють приблизно в такий спосіб:

(9.18)

де у (х) - точний розв’язок диференціального рівняння. Удосконалений метод Ейлера є більш точним у порівнянні з методом Ейлера та відноситься до методів 3-го порядку точності.

Схема алгоритму представлена на рисунку 9.8.

Рисунок 9.8 - Схема алгоритму удосконаленого метода Ейлера

Модифікований метод Ейлера заснований на використанні ітераційної формули виду:

(9.19)

Геометрична інтерпретація представлена на рисунку 9.9.

Рисунок 9.9 – Графічна інтерпретація

Алгоритм методу включає наступні кроки:

1. визначення похідної 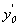в точці :

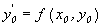
2. зміна незалежної змінної х за формулою:

3. визначення проміжного значення 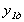за формулою методу Ейлера

4. визначення проміжної похідної в точці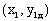

5. визначення середньо арифметичного значення двох похідних

6. визначення у₁ за формулою

ітераційний процес повторюється, починаючи з першого кроку.

Схема алгоритму метода представлена на рисунку 9.10.

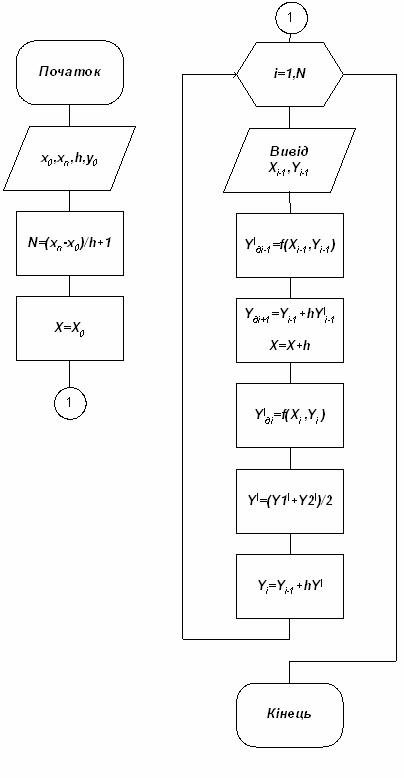
Рисунок 9.10 - Схема алгоритму модифікованого метода Ейлера

Удосконалений метод Ейлера - Коші з наступною ітераційною обробкою. Метод Ейлера - Коші з ітераційною обробкою є більш точним, чим, раніше розглянутий метод Ейлера - Коші. Сутність його полягає в тім, що виробляється ітераційна обробка кожного знайденого значення y_і. Спочатку вибирається грубе наближення потім будується ітераційний процес:

(9.20)

Ітерації продовжуються доти, поки два послідовних наближення не збіжаться до заданої похибки. Після цього приймається 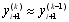. Якщо після трьох-чотирьох ітерацій, при обраному значенні h, збігу потрібних знаків не відбувається, то варто зменшити крок розрахунку h.

Дата добавления: 2014-11-08