Різницеві методи розв'язування диференційних рівнянь у частинних похідних

Класичне визначення похідної функції однієї змінної записується у вигляді

.

Природно, в ЕОМ не можна зробити граничного переходу. З іншого боку, можна додати деяке мале, хоча і ненульове, значення h і спробувати перевірити, що наближення виходить досить точним (проблема точності) і що помилка не зростає в ході процесу обчислень (проблема стійкості), тобто цей метод зводиться до того, що похідну заміняємо різницею.

Оскільки тепер є дві незалежні змінні, то обидві вони повинні брати участь у різницевому рівнянні. Розглянемо спочатку різниці в напрямку х.

Розклад функції 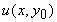в ряд Тейлора в околі точки (, ) можна записати у вигляді:

де 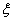лежить між х і х₀. Якщо тепер представити 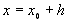, то після деяких перетворень одержуємо

Класичне визначення похідної функції однієї змінної можна записати:

.

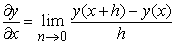Очевидно, на ЕОМ неможливо провести граничний перехід. А тому із розкладу функції в ряд Тейлора в околі точки 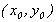можна наближено записати

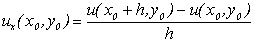(11.3)

з помилкою обмежування ; .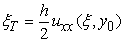

Вираз (11.3) називають правою різницею, а вираз

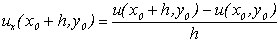(11.4)

лівою різницею.

Користуючись (11.3) та (11.4), можна отримати різницевий вираз для 2-ї похідної

(11.5)

і відповідно

, (11.6)

де h, k – величина кроку відповідно за координатами х та у.

Помилка обмеження дорівнює

.

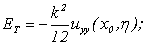
Аналогічно (11.5) і (11.6), можна вивести вираз для 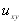. Використовуючи ці вирази, загальновідоме рівняння Лапласа , наприклад, можна записати в кінцевих різницях у вигляді:

(11.7)

Дата добавления: 2014-11-08