Параболічні рівняння

Лекція № 12

ЧИСЕЛЬНІ МЕТОДИ РОЗВ'ЯЗАННЯ ДИФЕРЕНЦІАЛЬНИХ РІВНЯНЬ У ЧАСТИННИХ ПОХІДНИХ (ЧАСТИНА 2)

Як приклад фізичної задачі, що приводить до рівняння цього типу, розглянемо процес теплопередачі по довгому стрижні, що лежить уздовж осі х від х = 0 до х = L. Припускаючи, що в точці х = 0 температура підтримується на рівні Те, а в тоці х = L температура підтримується на рівні Т_L. Припускаючи також, що в момент часу t = 0 розподіл температури уздовж стрижня задана функцією f (х). Тоді розподіл температури уздовж стрижня в усі наступні моменти часу отримується шляхом розв‘язку рівняння:

(12.1)

де і – температура стрижня в даній точці в даний момент часу, а постійна 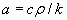, де с – теплоємність матеріалу стрижня, – щільність матеріалу стрижня і k – його теплопровідність. Для простоти припустимо а = 1, тоді рівняння зведеться до наступного вигляду:

, або 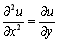. (12.2)

Граничними умовами для цього рівняння є:

(12.3)

і початковою умовою є:

. (12.4)

Рівняння (12.2) являє собою параболічне диференціальне рівняння в частинних похідних, відоме за назвою рівняння теплопередачі чи рівняння дифузії.

Багато інших важливих задач також приводять до параболічних рівнянь. Наприклад, рівняння, якими описуються довгі лінії зв'язку, так звані телеграфні рівняння, також є параболічними.

При записі в різницевій формі граничні умови запишуться так:

(12.5)

Початкова умова (12.4) запишеться у вигляді

. (12.6)

Щоб перетворити в різницеву форму (12.2), знову уявимо собі сітку, що охоплює область 0 < х < L і t > 0 з інтервалом розбиття k у напрямку х та інтервалом розбиття k у напрямку t. Використовуючи різницеві формули одержуємо:

, (12.7)

де , (12.8)

та індекс i змінюється від 1 до n -1, а індекс j – від 1 до 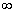. Верхня межа помилки обмеження виражається співвідношенням

, (12.9)

де , за умови 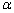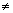1/6, тому що тоді це вираження перетворюється в нуль. При 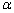=1/6 верхня межа помилки обмеження виглядає так:

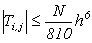, (12.10)

де .

Різницева схема представлена на рис. 12.2.

Рисунок 12.2 – Різницева схема для параболічного рівняння (випадок 1)

Очевидно, що з погляду найменшої помилки обмеження доцільно було б вибирати

(12.11)

Це не завжди виявляється зручним.

Метод, що привів до рівняння (12.7), був заснований на використанні правих різниць (11.3, 11.5). Якщо використовувати ліві різниці (11.4, 11.6), то різницеве рівняння запишеться в наступному вигляді:

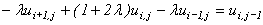(12.12)

де означає те ж, що й у (12.8).

Різницева схема цього методу виглядає так:

Рисунок 12.3– Різницева схема для параболічного рівняння (випадок 2)

Верхня межа помилки обмеження визначається формулою:

(12.13)

де .

Розглянемо ще один спосіб побудови різницевого рівняння, еквівалентного (12.12). Згадаємо, що, згідно (11.5), у точці (i, j)

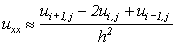
Аналогічно в точці (i, j+1)

Усереднюючи ці два наближення, одержимо

Якщо тепер для обчислення u_i скористатися правими різницями, то

і різницеве рівняння, еквівалентне (12.12), запишеться у вигляді

(12.14)

Цей спосіб побудови різницевого рівняння часто називають методом Кранка – Нікольсона.

Верхня межа помилки обмеження дається формулою

(12.15)

де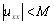

Ця верхня межа в 6 + 1 разів менше, ніж (12.13).

Рисунок 12.4– Різницева схема для параболічного рівняння (випадок 3)

Оскільки межа помилки обмеження (12.15) менше, то по цій характеристиці різницеве рівняння (12.14) переважніше, ніж (12.8).

Вище розглянуто три різних способи різницевого представлення диференціального рівняння и_хх = и_t а саме формули (12.7), (12.12) і (12.14). Розглянемо тепер методи розв’язання кожного з цих різницевих рівнянь і зіставимо їхні переваги і недоліки. В усіх випадках вважається, що граничні і початкові умови задані у вигляді (12.5) і (12.6).

Перший спосіб, обумовлений формулою (12.7), являє собою явну систему рівнянь для u_{i,j+ 1} у тому же самому сенсі, у якому (11.27) було явною системою для випадку гіперболічного рівняння. Маючи на підставі початкових і граничних умов перший ряд розв’язку, можна обчислити другий рядок, j = 1, безпосередньо з (12.3), при j = 0. Обчисливши другий рядок, можна в такий же спосіб обчислити третій рядок, поклавши цього разу j = 1. Таким же способом можна продовжувати обчислювати розв’язок настільки далеко по осі часу, яка у цьому є необхідність.

Ця ситуація цілком аналогічна тій, де були розглянуті гіперболічні рівняння. Тому природно очікувати, що для параболічних рівнянь повинні виникнути ті ж питання збіжності і стійкості. Так це і є в дійсності: процес обчислення рішення сходиться і стійкий, якщо

чи, те ж саме, при

Тим самим накладаються досить жорсткі обмеження на вибір кроку за часом, набагато більш жорсткі, ніж у випадку гіперболічного рівняння. Саме це і змушує шукати можливості розв’язки рівняння іншими способами, зокрема (12.12) і (12.14).

І (12.12), і (12.14) являють собою неявні методи розв’язання, аналогічні тому, що був застосований для еліптичних рівнянь. Розглянемо спочатку (12.12). Можна виписати рівняння для першого рядка розв’язку j =1, використовуючи початкові і граничні умови (12.3) і (12.4):

Усього виходить n - 1 лінійних рівнянь з п - 1 невідомими для i = 1,2,...,n-1. Ці рівняння можна вирішити методом виключення; крім того, що переважна більшість коефіцієнтів дорівнює нулю, сам вид системи робить рішення методом виключення досить просто. Справа в тім, що єдині ненульові коефіцієнти розташовані в трьох діагональних рядах симетрично щодо головної діагоналі. Система рівнянь цього типу називається тридіагональною. Можна вирішувати цю систему і за допомогою ітераційного методу Гаусса – Зейделя, тому що діагональний коефіцієнт у кожному рівнянні дорівнює 1 + 2 , а сума недіагональних дорівнює –2 , що забезпечує збіжність. Для прискорення збіжності можна скористатися екстраполяцією.

Знайшовши розв’язання для першого рядка, тобто для t = k, j = 1, можна записати систему рівнянь для другого рядка і знову одержати тридіагональну систему з n – 1 рівнянь. Після вирішення цієї системи можна переходити до третього рядка і так далі. Для обчислення одного рядка рішення щоразприходиться вирішувати систему з п – 1 лінійних алгебраїчних рівнянь.

Оскільки трудомісткість цього способу набагато більше, ніж для явних формул (12.7), можна задати собі питання, чи має сенс узагалі, прибігати до такого способу? Відповідь на це питання полягає в тім, що (12.12) стійке і сходиться для всіх > 0. Тому, використовуючи метод (12.12), можна брати набагато більшу величину кроку за часом. Спробуємо визначити, чи можна дійсно домогтися економії машинного часу.

Відомо, що при використанні методу (12.12) витрати машинного часу на обчислення одного рядка рішення будуть удвічі більше, ніж при використанні методу (12.7). Якщо взяти = 1, то загальна витрата часу на розрахунок рішення до визначеного моменту буде вдвічі менше. Правда, потрібно врахувати, що помилка обмеження круто зростає з ростом кроку за часом, так що визначальним фактором може з'явитися саме максимально припустима помилка.

Остання різницева формула (12.14) є іншим неявним методом і для обчислення одного рядка також вимагає рішення тридіагональної системи з n - 1 рівнянь. Витрати машинного часу при використанні цієї формули будуть, отже, такими ж, як і для (12.12). Цей метод також стійкий для всіх .

Помітимо, що при подвоєнні у формулі (12.14) помилка обмеження подвоюється, у той час як у (12.12) помилка обмеження збільшувалась в 4 рази. Тому метод (12.14) (метод Кранка - Нікольсона) кращий, ніж (12.12).

Потрібно відзначити, однак, що для інших параболічних рівнянь цей метод стійкий не при всіх і тому іноді приходиться прибігати до (12.12).

На рис. 12.5 представлено чотири різницеві схеми які використовуються для рівнянь другого порядку в частинних похідних.

Рисунок 12.5– Різницеві схеми, для еліптичного (а), гіперболічного (б) і параболічного (в, г)

Приклад розв’язку відомої інженерної задачі моделювання розподілу температури в трубі квадратного перетину

Розглянемо довгу квадратну трубу з квадратним отвором, по якій тече гаряча рідина. Труба наполовину занурена в крижану ванну, так що температура нижньої половини поверхні труби дорівнює 0°С. Верхня площина труби знаходиться при постійній температурі 100°С. Крім того, ми припускаємо, що температура зовнішньої поверхні труби лінійно змінюється від 0° С до 100° С на ділянці між крижаною ванною і верхньою площиною труби. Рідина усередині труби має температуру 200°С. Зовнішній розмір труби дорівнює 10 дюймам, внутрішній розмір дорівнює 4 дюймам. Поперечний переріз труби зображений на рис. 12.6.

Рисунок 12.6– Перетин труби в практичному прикладі

Розподіл температури в тілі труби задовольняє рівнянню в частинних похідних

,

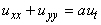де постійна 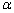враховує теплоємність, теплопровідність і щільність матеріалу труби. У даній задачі мі будемо приймати, що рідина тече протягом досить довгого часу для того, щоб усі перехідні процеси встигли

закінчитися, тобто тепловий режим труби став стаціонарним. Тоді і рівняння здобуває наступний вид:

Цьому рівнянню задовольняє розподіл температур усередині труби, а розподіл температур на границях труби задано граничними умовами. Таким чином, наша задача являє собою задачу Дирихле для рівняння Лапласа. Природно, мається на увазі двовимірна задача, тобто, наприклад, не враховується зниження температури рідини уздовж осі труби. Інакше кажучи, ми будемо обчислювати розподіл температури тільки для одного якогось перетину труби.

Припустимо, що по зовнішньому розмірі в напрямках х и у зроблена розбивка на 60 інтервалів, так що h = k = 0,16667 дюйма. Тоді граничні умови запишуться так:

Різницеві рівняння виглядають так:

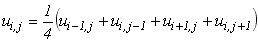
при

та

та

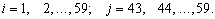
Ми можемо вирішити ці рівняння прискореним методом Лiбмана і знайти температуру у всіх внутрішніх крапках труби.

Формула прискореного методу Лiбмана переписана для цієї задачі в наступному виді:

Процес висновку результатів обчислень тут не показаний. Звичайно, можливо надрукувати обчислені значення температури для всіх 2856 внутрішніх точок, але намагатися зрозуміти що-небудь з цієї маси чисел зовсім безнадійно.

У даному випадку більш наглядним прикладом розв’язком даної задачі з'явився би рисунок карти ізотерм (ліній постійної температури) у перетині труби за допомогою ЭЦВМ. Така карта приведена на рисунку 12.7. Ця карта надрукована за допомогою спеціальної програми та відповідає таблиці 12.1, у якій приведена температура, зображувана різними ізотермами. Наприклад, з цієї таблиці ясно, що символ А відповідає діапазонові температур від 0° С до 11.7°С. Звичайно, якщо потрібно більш докладна картина, то можна вивести на друк всі значення температури для внутрішніх точок труби.

Загальна інформація такого типу, як карта ізотерм, часто є головною метою початкової фази досліджень за допомогою ЕОМ. Нерідко в подібних випадках потрібно багаторазово вирішувати ту саму задачу, варіюючи значення деякого параметра; у результаті загальна залежність розподілу температури від цього параметра наочно видна на діаграмах.

Таблиця 12.1 Мнемонічні представлення для карти ізотерм

Символ	Діапазон температури °С
A	0 – 11.7
B	23.6 – 35.3
C	47.1 – 58.7
D	70.6 – 82.3
N	94.2 – 105.8
O	117.9 – 129.4
P	141.4 – 152.9
Q	164.8 – 176.3
R	188.3 – 200.0

Нарешті, спробуємо оцінити, наскільки ефективним може виявитися метод прискорення. На рисунку 12.8 побудований графік залежності кількості ітерацій, необхідних для того, щоб розв’язок задачі зійшовся, від прискорюючого множника .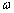

Рисунок 12.7– Карта ізотерм для труби.

Помітимо, що оптимальним значенням для 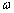є приблизно 1.8, а при віддаленні від цього оптимального значення в ту або іншу сторону кількість необхідних ітерацій збільшується. Для 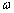= 1, тобто

при використанні звичайного методу Либмана, кількість необхідних ітерацій приблизно в сім разів більше, ніж при оптимальному .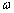

Рисунок 12.8 – Кількість ітерацій, необхідне для збіжності обчислень як функцій множника 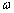, що прискорює (практичний приклад).

Дата добавления: 2014-11-08