Порівняння методів одновимірного пошуку

Найкращими критеріями порівняння методів пошуку, які були описані вище, є їх ефективність і універсальність. Під ефективністю алгоритму розуміють число обчислень функції, необхідне для досягнення необхідного звуження інтервалу невизначеності. Із табл. 13.1 видно, що найкращим в цьому відношенні є метод Фібоначчі, а найгіршим – метод загального пошуку. Конструктор не з великим задоволенням використовує метод Фібоначчі, так як при його застосуванні необхідно заздалегідь задавати число обчислень значень функції. Однак він може скористатися методом золотого перетину. Як правило, методи Фібоначчі і золотого перетину, володіють високою ефективністю, найбільш підходять для розв’язку одновимірних унімодальних задач оптимізації.

Універсальність алгоритму означає, що його можна легко застосувати для розв’язку самих різноманітних задач. В цьому відношенні метод Фібоначчі, поступається іншим, так як потребує окремого обчислення положення точок, в яких будуть визначатися значення цільової функції на кожному новому кроці. Цим приходиться розплачуватися за підвищення ефективності метода. З точки зору універсальності малоефективний метод загального пошуку має по крайній мірі одну перевагу – його можна з успіхом застосовувати і для неунімодальних функцій, якщо вони достатньо гладкі. Нерідко заздалегідь не відомо, чи є розглянута цільова функція унімодальною. В таких випадках слід використати декілька різних алгоритмів і подивитись, чи дають вони усі один і той самий оптимум. Звідси витікає важливий висновок, який слід мати на увазі, розв’язуючи задачі оптимізації: не існує універсального алгоритму, який дозволяв би розв’язувати будь-які задачі. Вирішуючи складні задачі оптимізації, слід користуватися різними методами, так як це дозволяє збільшити долю вигідних розв’язків.

Таблиця 13.1 Порівняння методів одновимірного пошуку по значенням коефіцієнта дроблення інтервалу невизначеності f

Кількість обчислень цільової функції N	Загальний пошук	Ділення відрізка навпіл	Метод дихотомії	Метод золотого перетину	Метод Фібоначчі
	1,0 0,667 0,500 0,400 0,333 0,286 0,250 0,222 0,200 0,182 0,167 0,154 0,143 0,133 0,125 0,118 0,111 0,105 0,100 0,095	1,0 - 0,500 - 0,250 - 0,125 - 0,0625 - 0,0312 - 0,0156 - 0,00781 - 0,00391 - 0,00195 -	1,0 0,500 - 0,250 - 0,125 - 0,0625 - 0,0312 - 0,0156 - 0,00781 - 0,00391 - 0,00195 - 0,000976	1,0 0,618 0,382 0,236 0,146 0,090 0,056 0,345 0,0213 0,0132 0,00813 0,00502 0,00311 0,00192 0,00119 0,000733 0,000453 0,000280 0,000173 0,000107	1,0 0,500 0,333 0,200 0,125 0,077 0,048 0,0294 0,0182 0,0112 0,00694 0,00429 0,00265 0,00164 0,00101 0,000626 0,000387 0,000239 0,000148 0,0000913

Приклад 1. Одновимірна мінімізація в середовищі Mathcad

Для знаходження мінімуму одновимірної функції в середовищі Mathcad використовується функція root(f(var1, var2,...),var1, [a, b]) – повертає змінну var1, що лежить між a і b, в якій функція, що розв’язується дорівнює нулю.

Параметри:

f – рівняння, яке потрібно розв’язати;

var1 – корінь рівняння;

[a, b] – відрізок, на якому шукається розв’язок рівняння.

Наприклад, необхідно знайти мінімум гладкої унімодальної функції у=х²+е^х, використовуючи необхідну умову мінімуму.

Визначимо цільову функцію

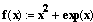
Визначимо першу похідну цільової функції

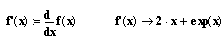
Визначимо другу похідну цільової функції

Достатня умова унімодальності (f''(x)>0) виконана

Мінімум гладкої функції досягається в стаціонарній точці (f'(x)=0).

Розв’яжемо рівняння f'(x)=0, використовуючи функцію root; початкове наближення кореня нехай дорівнює нулю (х=0)

Точка мінімуму х=-0.351732

Значення функції в точці мінімуму

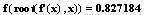
Підтвердимо результати обчислень графічно

Дата добавления: 2014-11-08