Рентгеновские спектры

Самым распространенным источником рентгеновского излучения является рентгеновская трубка, в которой сильно ускоренные электрическим полем электроны бомбардируют анод. При торможении электронов возникает рентгеновское излучение. Спектральный состав рентгеновского излучения представляет собой наложение сплошного спектра, ограниченного со стороны коротких волн граничной длиной 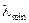, и линейчатого спектра – совокупности отдельных линий на фоне сплошного спектра.

Сплошной спектр обусловлен излучением электронов при их торможении. Поэтому его называют тормозным излучением. Максимальная энергия кванта тормозного излучения соответствует случаю, когда вся кинетическая энергия электрона переходит в энергию рентгеновского фотона, т.е.

,

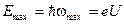где U – ускоряющая разность потенциалов рентгеновской трубки.

Отсюда граничная длина волны

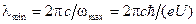. (23.6.1)

Измерив коротковолновую границу тормозного излучения, можно определить постоян­ную Планка. Из всех методов определения 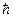данный метод считается самым точным.

При достаточно большой энергии электронов на фоне сплошного спектра появ­ляются отдельные резкие линии. Линейчатый спектр определяется только материалом анода, поэтому данное излучение называется характеристическим излучением.

Характеристические спектры отличается заметной простотой. Они состоят из нескольких серий, обозначаемых буквами K, L, M, N и O. Каждая серия насчитывает небольшое число линий, обозначаемых в порядке возрастания частоты индексами a, b, g … (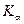, , 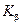, 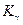…; , 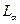, , 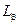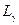… и т.д.). Спектры разных элементов имеют сходный характер. При увеличении атомного номера Z весь рентгеновский спектр целиком смещается в коротковолновую часть, не меняя своей структуры (рис.). Это объясняется тем, что рентгеновские спектры возникают при переходах внутренних электронов, которые для разных атомов являются сходными.

Схема возникновения рентгеновских спектров дана на рис. Возбуждение атома состоит в удалении одного из внутренних электронов. Если вырывается один из двух электронов K -слоя, то освободившееся место может быть занято электроном из какого-либо внешнего слоя (L, M, N и т.д.). При этом возникает K -серия. Аналогично возникают и другие серии, наблюдаемые, впрочем, только для тяжелых элементов. Серия K обязательно сопровождается остальными сериями, так как при испускании ее линий освобождаются уровни в слоях L, M и т.д., которые будут в свою очередь заполнятся электронами из более высоких слоев.

Исследуя рентгеновские спектры элементов, Г. Мозли установил соотношение, называемое законом Мозли

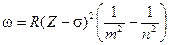, (23.6.2)

где w – частота линии характеристического рентгеновского излучения, R – постоянная Ридберга, 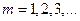(определяет рентгеновскую серию), 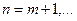(определяет линию соответствующей серии), s – постоянная экранирования.

Закон Мозли позволяет по измеренной длине волны рентгеновских линий точно установить атомный номер данного элемента; этот закон сыграл большую роль при размещении элементов в периодической таблице.

Дата добавления: 2014-11-18