Моменты инерции плоского сечения

Моменты инерции бывают: осевые или экваториальные – формулы (3.4), полярный – (3.5) и центробежный – (3.6)

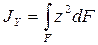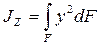; ; (3.4)

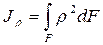; (3.5)

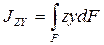. (3.6)

Если начало координат совпадает с полюсом, то 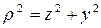, следовательно

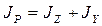. (3.7)

Размерность моментов инерции – единица длины в четвёртой степени (например, см⁴). Отметим, что осевой и полярный моменты инерции всегда положительны. Центробежный момент инерции может быть положительным или отрицательным в зависимости от положения осей.

Оси координат, проходящие через центр тяжести сечения, называются центральными.

Центральные оси, относительно которых центробежный момент инерции равен нулю – называются главными центральными осями. Признак главных центральных осей – если две взаимно перпендикулярные оси проходят через центр тяжести сечения и при этом хотя бы одна из них является осью симметрии сечения, то эта пара осей главная.

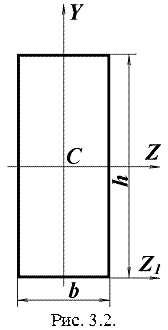
Ниже приведена формула для определения моментов инерции относительно главных осей прямоугольника. С – центр тяжести сечения, оси z и y – главные оси инерции сечения. Формулы для определения моментов инерции записываем без вывода:

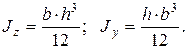(3.8)

При практических расчетах возникает необходимость пересчета моментов инерции сечения с одних осей на другие. Переход от одной системы координат к другой можно осуществить путем двух «движений». Путем параллельного переноса осей совмещаем начала координатных осей, а затем производим их поворот на необходимый угол до совмещения осей (рис. 3.3).

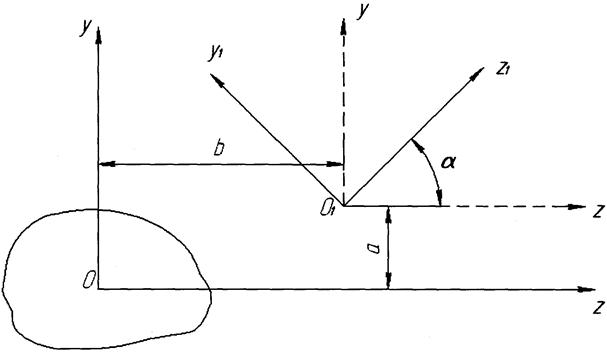
Рис. 3.3.

Для краткости изложения и с учетом того факта, что при выводе выражений используется известный из аналитической геометрии математический аппарат, формулы далее приводим без вывода.

Дата добавления: 2014-11-18