Аксиоматические методы. 3 страница

Покажем на примере вычисление вектора глобальных приоритетов. Полные примеры решения задач – в Справке СППР NooTron (http://nootron.net.ua).

1 Пусть число критериев m=4 и вектор локальных приоритетов критериев имеет вид:

(0.4; 0.3; 0.2; 0.1), сумма компонентов = 1.

2 Пусть число альтернатив n=3, их 4 вектора локальных приоритетов имеют вид (4 вектора – потому что у нас 4 критерия и, соответственно, 4 матрицы парных сравнений альтернатив по критериям):

(0.15; 0.44; 0.41),

(0.22; 0.31; 0.47),

(0.46; 0.33; 0.21),

(0.19; 0.39; 0.42).

И здесь все суммы равны 1.

3 Составляем три вектора оценок альтернатив по критериям (т.е. их профили). Легко заметить, что это – наши столбцы:

(0.15; 0.22; 0.46; 0.19) – оценка 1-й альтернативы по всем 4-м критериям,

(0.44; 0.31; 0.33; 0.39) – оценка 2-й альтернативы,

(0.41; 0.47; 0.21; 0.42) – оценка 3-й.

Здесь суммы компонентов, конечно, не всегда будут равны 1.

4. Находим три скалярных произведения. Вспоминаем, что скалярное произведение – это число, равное сумме парных произведений компонент с одинаковыми номерами в векторе (1-ю на 1-ю, 2-ю на 2-ю и так m раз, а потом сложить). Первый сомножитель у нас один и тот же. Это вектор локальных приоритетов критериев (0.4; 0.3; 0.2; 0.1). Вторые сомножители – наши последние вектора.

1) (0.15; 0.22; 0.46; 0.19)

0.4x0.15+0.3x0.22+0.2x0.46+0.1x0.19 = 0.237

2) (0.44; 0.31; 0.33; 0.39)

0.4x0.44+0.3x0.31+0.2x0.33+0.1x0.39 = 0.374

3) (0.41; 0.47; 0.21; 0.42)

0.4x0.41+0.3x0.47+0.2x0.21+0.1x0.42 = 0.389

0.237+0.374+0.389 = 1.

Сумма компонентов равна 1, нормировать не надо, мы сразу получили решение задачи – вектор глобальных приоритетов: (0.237; 0.374; 0.389).

Иногда полученный вектор глобальных приоритетов дополнительно нормируют на максимум и выражают в процентах относительно лучшей альтернативы. Для нашего примера имеем: (60.9%; 91.6%; 100%).

Но это – лишь в окончательном ответе, не в промежуточных расчётах!

5. Анализ результатов. Мы видим, что у нас лучшей оказалась третья альтернатива, вторая немного хуже. Явного победителя нет. Поэтому, вообще говоря, следовало бы провести дополнительное сравнение этих двух альтернатив, отбросив первую. Второй путь: добавить новые, менее важные критерии.

6. Анализ резуьтатов и выводы в МАИ. Вычисленные векторы локальных приоритетов, профили альтернатив, их вектор глобальных приоритетов – математическое решение поставленной задачи.

Вектор локальных приоритетов уровня критериев показывает их важность относительно цели исследования. Совместно с профилем интересующего нас объекта (альтернативы) он показывает направления совершенствования этого объекта, отображая важность каждого из свойств или параметров («что важно и чего недостаёт объекту в сравнении с другими»). Это особенно важно при проектировании, модернизации, оценках конкурентоспособности.

Векторы локальных приоритетов уровня альтернатив дают относительные числовые характеристики объектов по каждому из критериев, что также важно для выбора направлений модернизации, повышения конкурентоспособности.

Вектор глобальных приоритетов позволяет произвести ранжирование объектов относительно цели по всей совокупности рассмотренных критериев: каждой альтернативе соответствует свой приоритет (компонента вектора) – число в интервале (0…1). Чем это число больше, тем объект предпочтительнее. Это позволяет решить задачу рационального многокритериального выбора: альтернатива с наибольшим глобальным приоритетом является лушей по совокупности рассмотреных критериев.

Вектор глобальных приоритетов можно использовать в качестве критерия обобщенной ценности в задачах распределения ресурсов. Если в состав альтернатив включить лучшие из известных объектов данной отрасли, то, вычислив приоритеты, можно определить уровень предлагаемых технических, организационных и бизнес-проектов.

К настоящему времени разработано много вариантов метода анализа иерархий. Мы изучили классический вариант метода – МАИ в «относительных измерениях» (дескриптивный МАИ). В библиотеке методов СППР NooTron также содержатся: МАИ в «абсолютных измерениях» (нормативный МАИ) и обобщение МАИ – метод анализа сетей (МАС), или analytic network process (ANP). Он разработан Т.Л. Саати для анализа решений в иерархиях с горизонтальными и обратными связями и в сетевых структурах. Эти методы предлагаются для самостоятельного изучения, их можно использовать при выполнении контрольного задания.

Контрольные вопросы

1) Метод анализа иерархий: сущность, условия, основные задачи.

2) Базовая иерархическая структура метода анализа иерархий.

3) Построить 3-уровневую полную доминантную иерархию МАИ.

4) Построить 4-уровневую полную доминантную иерархию МАИ.

5) Парные сравнения в МАИ и шкала Саати, построить матрицу парных сравнений.

6) Пояснить свойства матрицы парных сравнений, построив её.

7) Каково количество матриц парных сравнений для 3-уровневой иерархии: 1 цель, m критериев и n альтернатив?

8) Главное собственное число и собственный вектор матрицы парных сравнений.

9) Локальные приоритеты и методы их вычисления.

10) Построить матрицу парных сравнений 3-го порядка, упрощённо вычислить её локальные приоритеты.

11) Согласованность, индекс и отношение согласованности в МАИ.

12) Глобальные приоритеты и их вычисление, пример вычисления.

13) Анализ результатов в МАИ: что показывают локальные и глобальные приоритеты.

14) Придумать и сформулировать задачу выбора в терминах МАИ, построить матрицы парных сравнений для неё.

15) Основные системные задачи, где применяется метод анализа иерархий.

16) Какие виды иерархий Вы знаете? Назвать уровни иерархии. Какая иерархия называется доминантной полной иерархией? Привести пример 3-х или 4-х уровневой иерархии.

2.2.3. Метод взвешенных сумм и его аналоги

Характеристика метода взвешенных сумм

Метод взвешенных сумм, МВС относится к прямым методам количесвенного анализа решений. В англоязычной литературе он часто называется Simple Additive Weighting (SAW) – простое аддитивное взвешивание. В своих разнообразных вариантах МВС широко применяется на практике. Он программно реализован в СППР NooTron.
Достоинства и недостатки МВС «зеркальны» МАИ (п. 2.2.2). Метод взвешенных сумм позволяет работать с большим (в принципе – неограниченным) числом критериев сложной древовидной иерархической структуры (многоуровневая доминантная иерархия) и неограниченным в принципе количеством сравниваемых объектов (альтернатив). Недостаток метода в базовом варианте – невысокая в сравнении с МАИ точность. МВС используется в основном для составления всевозможных рейтингов и для классификации объектов на основе рейтинга. Для ответственного выбора лучше применять МАИ.

Алгоритм метода взвешенных сумм

Математика основного варианта МВС сумм весьма проста.

На каждом «кусте» древовидной струкуры промежуточная оценка альтернативы (то есть её функция полезности) рассчитывается по формуле взвешенной суммы:

,

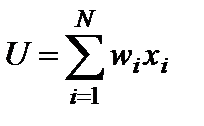где 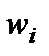— вес (важность) 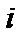-го критерия, назначаемый ЛПР; 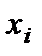— оценка альтернативы по 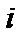-му критерию.

Заметим, что это – скалярное произведение вектора весов (локальных приоритетов) критериев на вектор оценок альтернативы (на данном уровне).

Сумма весов критериев в методе взвешенной суммы должна быть нормирована на единицу:

.

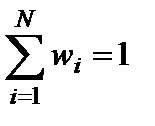Иногда этот метод используют при одинаковых весах критериев . Это – метод простой суммы. Если при этом , , а 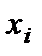, измеряется в целых числах (баллах), то такой вариант называется балльным методом.

Логическим обоснованием метода взвешенной суммы является представление об общей полезности альтернативы как о сумме оценок по нескольким независимым критериям. Коэффициенты 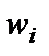выражают относительную важность оценок критериев. Существуют различные способы определения весов: экспертный (индивидуальный и групповой), с использованием методы анализа иерархий и ранжированных весов. Первичные оценки альтернатив делаются на самом нижнем уровне иерархии экспертно, либо по утверждённым методикам. Часто используются балльные оценки. Рекомендуется для всех критериев нижнего уровня («листьев дерева») применять единую балльную шкалу, например 1…10, 1…12.

Система критериев в МВС чаще всего имеет многоуровневую разветвлённую иерархическую структуру (для простых иерархий лучше использовать МАИ). В иерархии МВС расчёт глобального показателя (рейтинга) альтернативы идёт от листьев по ветвям к единой вершине – корню дерева иерархии, где и получается результат – глобальный приоритет (ГП). И так по всем альтернативам. На основании расчитанных глобальный приоритетов формируется общий рейтинг рассматриваемых объектов: список альтернатив с указанием их глобальных приоритетов, упорядоченный по убыванию ГП. Таким образом, из n альтернатив объект с наибольшим ГП получает № 1, а с наименьшим - № n.

Процесс оценка альтернатив методом взвешенной суммы называется скорингом, от английского to score – подсчитывать очки, баллы. Результаты оценки – рейтинги, (rating – оценка, определение ценности). Рейтинг вуза, рейтинг студента. На основании рейтингов производится классификация, распределеие по категориям. Понятно, что метод взвешенных сумм используется на практике широко: рейтинги стран, фирм, вузов, студентов...

В библиотеке методов СППР NooTron содержатся метод взвешенных сумм с несколькими вариантами выбора весов критериев.

Мультипликативный метод

Здесь глобальная функция полезности альтернативы на каждом уровне иерархии – это произведение «частных» функций полезности с учётом их весов:

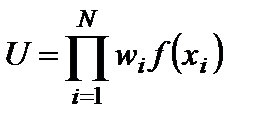
Чаще всего принимают . Реже используют зависимость 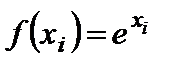. Путем логарифмирования мультипликативный метод можно свести к суммированию логарифмов оценок, поэтому иногда его объединяют с методом взвешенных сумм. Логическим обоснованием мультипликативного метода является представление об оценках по критериям, как о вероятностях достижения определенных показателей качества.

Метод ранжирования (упорядочения) критериев

В данном методе критерии упорядочиваются по важности, после чего веса критериев определяются только их позицией (номером) в упорядоченном списке. Иногда считается лучшей альтернатива, имеющая более высокую оценку по более важному критерию вне зависимости от оценок по прочим критериям (то есть здесь вес первого критерия равен 1, а остальных 0). В библиотеке методов СППР NooTron он содержится как часть метода взвешенных сумм, используется для определения весов критериев.

Методы сравнения разностей оценок альтернатив

Пусть , 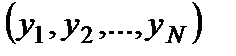— оценки альтернатив и по 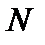критериям. Тогда в этом методе альтернатива предпочтительней, чем альтернатива , если

где 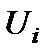— функция полезности для -го критерия, (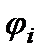 — функция, определяющая влияние разностей оценок по -му критерию на результат сравнения двух альтернатив.

Показано, что метод сравнения разностей оценок совпадает с методом взвешенных сумм, если в первом из них все функции линейны.

Контрольные вопросы

1) Провести сравнение метода анализа иерархий и метода взвешенной суммы.

2) Методы простой и взвешенной суммы, скоринг и рейтинг.

3) Придумать пример определения рейтинга методом взвешенной суммы.

4) Придумать пример определения рейтинга методом простой суммы.

5) Мультипликативный метод и его связь с методом взвешенных сумм.

2.2.4.

2.2.5. Методы матрицы решений и дерева решений

Метод матрицы решений

Для этого метода и его аналогов исходная информация по проблеме аккумулируется в специальной таблице – матрице решений (табл. 2.5).

Таблица 2.5 – Матрица решений

Альтерна-тивы	Варианты внешних условий
		…
			…
…	…	…	…	…

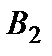
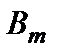
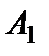
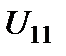
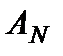
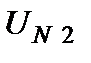
Элементы матрицы решений называются полезностями (utilities). Полезности – это некоторые количественные оценки (например, в деньгах или в натуральных показателях) результата принятия решения (выбора конкретной альтернативы) при том или ином варианте внешних условий, характеризующих обстановку после принятия решений.

Возможны два случая:

1) вероятности внешних условий заранее известны (ситуация риска);

2) вероятности внешних условий заранее неизвестны (ситуация неопределённости).

Но в любом случае считается, что сама таблица известна при принятии решений (весьма сильное предположение).

Выбор лучшей альтернативы (с полезностью ) производится на основании одного из следующих критериев:

1) Максиминный критерий (наибольшая осторожность). Выбирается:

где 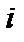— индекс строки, — индекс столбца таблицы.

2) Критерий, минимаксного сожаления. Вводится понятие сожаления для 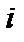-й альтернативы при -м варианте внешних условий:

,

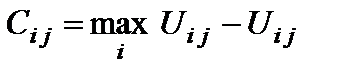Далее выбирается:

,

3) Критерий максимакса (крайний оптимизм)

,

4) Критерий Гурвица. Пусть для 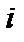-й альтернативы

, .

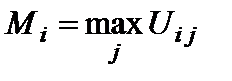Для каждой альтернативы вычисляют показатель:

,

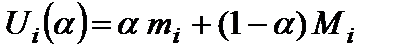где .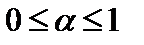

Далее выбирается (при заданном )

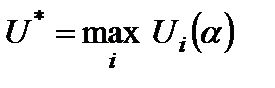
5) Критерий Лапласа. Все варианты внешних условий принимаются равновероятными и для каждой альтернативы определяется показатель

Далее выбирается:

.

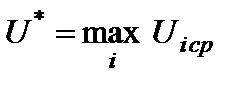Обычно нет особых оснований априорно считать один критерий чем-то лучшим, чем другой. Поэтому принято, что такой выбор должен делать руководитель. Тем более, что он всегда прав (или так думает). Если исключить очевидные случаи (доминирование одной альтернативы над всеми), то для ЛПР выбор критерия столь жетруден, как и прямой выбор одной из альтернатив. В решении сложных и ответственных проблем исследование надо проводить по нескольким критериям.

Метод дерева решений

В англоязычной литературе иногда этот метод называют «наука о решениях» (decision science). Хотя, конечно, это лишь один из методов науки о принятии решений и не более того. Этот метод связан с оценкой вероятностей внешних условий и математических ожиданий эффектов (полезностей или рисков) на специальных графах - деревьях решений. Основную идею данного подхода рассмотрим на ростом ппримере. Имеются два варианта действи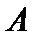й: и 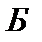(например, разрабатывать одну либо другую технологию производства нового продукта). Пусть при выборе варианта 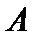точный результат заранее неизвестен и возможны три альтернативных исхода 1, 2, 3, привлекательность которых может быть оценена в деньгах: . Предположим, что известны вероятности этих исходов: . Тогда полезность варианта 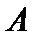определяется по формуле (ожидаемая денежная оценка):

.

Аналогично оценивается полезность варианта 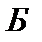. Выбор между 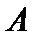и 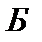должен соответствовать большему значению полезности.

Остаются две проблемы: как заранее определить все возможные исходы различных действий – для этого строится так называемое дерево решений; как определить вероятности исходов – для этого используется метод лотерей.

Деревья решений строят, исходя из последовательного анализа всех возможных событий. Примером может служить небольшое дерево на рис. 2.

Более интригующим является вопрос о том, как получить субъективные вероятности («шансы»). Это - вероятности, назначаемые ЛПР и экспертами, ведь статистики неизвестных событий у них практически нет.

Ответ на это сформулирован следующим образом. Пусть 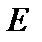— некоторое случайное событие реального мира, а 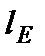— лотерея, которая дает выигрыш , если 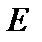произойдет и выигрыш — в противном случае. Если ЛПР не может определить, что для него лучше — лотерея 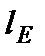или лотерея, дающая с вероятностью и L с вероятностью , то субъективная вероятность 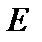принимается равной .

Итак, определение субъективных вероятностей событий производится путем поиска безразличия между двумя лотереями подбором вероятности осуществления событий в одной из них.

Подход применим как при оценках альтернатив по одному критерию, так и при многокритериальных альтернативах.

Рисунок 2.2

Основные прикладные задачи многокритериального анализа

Базовой задачей многокритериального анализа является ранжирование. Альтернативы, занимающие область в многомерном пространстве критериев в результате многокритериального ранжирования (например, методом анализа иерархий или методом взвешенных сумм) становятся линейно упорядоченными – от «лучшей» к «худшей».

Решение задачи ранжирования служит основой для решения более сложных и комплексных проблем (системных задач). В этой лекции рассмотрим основные из них.

1 Выбор одной или нескольких альтернатив, лучших по совокупности критериев.

2 Кластеризация и классификация.

3 Многокритериальная оптимизация.

4 Проектирование по количественным и качественным критериям.

5 Анализ эффективности проектов.

6 Распределение ресурсов.

7 Управление проектами.

Контрольные вопросы

1) Метод матрицы решений, построить и объяснить матрицу решений.

2) Критерии максимального оптимизма и гарантированного результата; построить матрицу решений и вычислить.

3) Критерий Гурвица; построить матрицу решений и вычислить.

4) Критерии Лапласа и Байеса-Лапласа; построить матрицу решений и вычислить.

5) Критерий минимаксного сожаления (критерий Сэвиджа); построить матрицу решений и вычислить.

6) Критерий Ходжа-Леманна; построить матрицу решений и вычислить.

7) Сущность метода дерева решений.

8) Сущность метода компенсаций.

9) Сущность метода порогов несравнимости.

10) Множество Парето, показать пример на плоскости 2-х критериев для 7-ми объектов.

11) Основные идеи интерактивных методов, их связь с прикладным системным анализом.

2.3. Информация и экспертные знания в системном анализе

2.3.1. Основы семантической теории информации

Определение понятия информации

Существует ряд определений, но до сих пор нет общепризнанного. Вместе с тем информация играет в науке все более фундаментальную роль: в кибернетике, компьютерных науках, системных науках, биологии, даже в таких науках как физика (кибернетическая физика) и механика.

Прикладное значение информации очевидно. Перейдем к существующим определениям.

«Информация есть информация, а не материя и не энергия» (Н.Винер).

«Материя и энергия – сохраняемые сущности реального объекта, а информация – несохраняемая сущность, она связана со структурой объекта и её изменениями, процессами (Жилин).

В гуманитарных науках часто используется тавтологическое определение: «информация есть сведения, знания, переданные кем-то другим или приобретенные собственным путем исследования или изучения…»

«Информация – это сведения, содержащиеся в сообщении, объекте передачи, хранении, обработке».

Иногда информацию связывают с упорядоченностью:

«Информация означает порядок, создания порядка из беспорядка, увеличение степени порядка после построения сообщения».

Философы часто определяют информацию как отражение

«Информация – это отражения в сознании людей причинно-следственных связей в окружающем мире».

«Информация – это содержание процессов отражения».

Информацию определяют и как алгоритм:

«Информация есть некий алгоритм, совокупность примеров правил и сведений».

Можно сделать вывод, что общепринятого определения информации всё ещё нет.

Синергетика (наука о процессах самоорганизации) внесла свой вклад, поскольку в ней информация: а) используется в исследовании процессов самоорганизации; б) здесь актуален вопрос о возникновении и эволюции ценной информации.

Понятие ценной информации является очень важным и для системного анализа. Его мы рассмотрим позже, а сейчас – два определения информации, важные именно для синергетики и системного анализа.

Определение Г. Кастлера:

«Информация есть случайный и заполненный выбор одного варианта из нескольких возможных и равноправных».

Но это определение не исчерпывает всех случаев, и поэтому Д.С. Чернавский уточнил определение Кастлера.

Определение информации по Д.С. Чернавскому:

«Информация - есть запомненный выбор одного варианта из нескольких возможных и равноправных».

Здесь исчезло слово «случайный», поскольку выбор может быть как случайным, так и неслучайным, сделанным, например, под внешним воздействием. Или, добавим от себя, выбор как результат решения проблемы: решил – и сделал выбор.

Согласно Д.С. Чернавскому, неслучайный выбор – это рецепция (приём) информации, а случайный выбор – генерация информации. В любом из этих случаев если информация не запоминается, то это – микроинформация, а запомненный выбор - макроинформация.

Возможный и равноправный выбор – это значит, что варианты выбора принадлежат одному множеству (например, слов одного языка, букв одного алфавита) и априорные (заранее предполагаемые) различия между ними невелики.

Количество информации

Понятие «количество информации» сформулировано в работах американских учёных Хартли и (особенно) Шеннона. Оно является центральным в «классической» теории информации, основная проблема которой – изучение передачи информации по каналам связи, хранения её, кодирования и декодирования, борьбы с шумами и помехами. Отметим – безотносительно к смыслу (семантике) передаваемых сообщений. В настоящее время развиваются и другие разделы теории информации – динамическая теория информации, семантическая теория информации, теория квантовой информации. Но в их основе находится теория информации Шеннона и её методы измерения количества информации. Мы рассмотрим основные формулы, относящиеся к передаче информации в дискретном (цифровом, алфавитном) виде. Сейчас – это основной метод работы с информацией. Да и формулы проще, чем в «непрерывной» теории.

По К. Шеннону количество информации I_N в сообщении, содержащем N символов определяется по формуле:

(1)

M - число букв (символов) в используемом алфавите;

p_i - частота (статистическая вероятность) появления i-той буквы в языке сообщения;

минус – чтобы величина I_N была неотрицательной.

Двоичные логарифмы используются в теории информации исходя из естественного требования, чтобы в минимальном сообщении содержалось количество информации, равное 1. Минимальный алфавит состоит из двух символов, например 0 и 1 (меньше нельзя): M=2, минимальное сообщение – из одного символа N=1, частоты символов равны: Pi= .

Подставив эти значения в формулу (1) действительно получим 1:

I₂= -1 ( (-1) + (-1)) = 1.

Дата добавления: 2014-11-18