Приклад 8.3

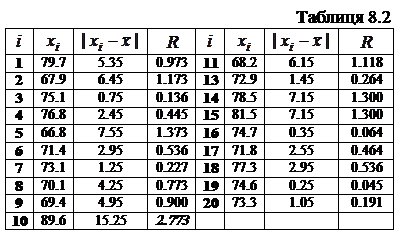
Из данных примера 8.2 необходимо исключить обнаруженную грубую ошибку, проверить полученный статистический ряд на наличие грубой ошибки, если она присутствует, исключить и ее и т. д., пока с вероятностью не менее 0.95 можно утверждать, что таких ошибок нет. Сравнить средние значения и СКО исходного ряда с очищенным.

Розв‘язання.

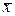Найдем оценки среднего значение и СКО 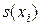. Получим: 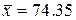и 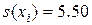. Значения статистик, как и следовало ожидать, существенно изменились. В табл. 8.2 приведены результаты расчетов

Находим по таблице Б.5 для 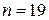и уровня значимости 0.05 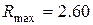. По результатам измерений после исключения первой грубой ошибки условие 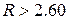выполняется только для одного результата, а именно, для 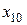. То есть 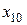тоже необходимо исключить из дальнейшего анализа. Сделаем это.

Находим по выборке объемом 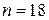среднее значение и СКО: .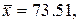

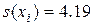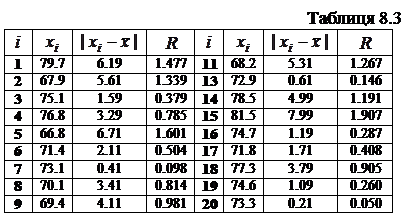
В табл. 8.3 приведены результаты измерений и расчетов после удаления двух грубых ошибок: 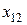и .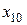

По табл. Б.5 при 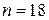и уровне значимости 0.05 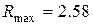. Результаты проведенного анализа показали, что после удаления двух грубых ошибок с вероятностью не меньше 0.95 в выборке нет больше промахов. Если по засоренной грубыми ошибкам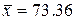и и 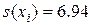, то более достоверными являются значения 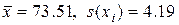. В данном случае исключение грубых ошибок наиболее существенно повлияло на СКО и, следовательно, дисперсию.

É

Для определения «промахов» существуют и другие методы, которые мы здесь не рассматриваем, но при желании их всегда можно найти в литературе по статистической обработке результатов эксперимента.

8.3.5. Доверительный интервал оценки измеряемой величины

После того как в серии измерений остались лишь достоверные результаты, можно рассчитать доверительную ошибку 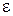и доверительный интервал для единичной 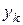или средней 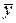оценки измеряемой величины. Истинное значение измеряемой величины с наперед заданной доверительной вероятностью должно лежать в пределах доверительных интервалов:

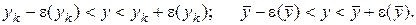
Для определения доверительного интервала единичного 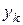и среднего 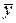результатов используется критерий Стьюдента :

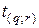Критерий 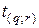берется из соответствующих таблиц (табл. Б.2 в зависимости от принятого уровня значимости 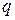и числа степеней свободы 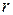, имевших место при определении дисперсии.

Свойства распределения Стьюдента и вытекающие из них свойства 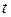- критерий Стьюдента 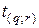описаны в приложении Б, комментарий к табл. Б.2.

Мы рассмотрели самые простые статистики случайных величин и, следовательно, в какой то мере и случайных процессов, например, сигналов. Фактически мы ограничились только двумя статистиками: математическое ожидание (среднее значение) и дисперсия (СКО). Это значит, что все рассмотренное выше, строго говоря, применимо только к тем случайным величинам, которые подчиняются нормальному распределению. В радиотехнике и телекоммуникации, кроме нормального закона, приходится иметь дело со случайными величинами, подчиняющимися другим законам. Это распределения Релея и Пуассона, закон арксинуса, равномерное распределение, показательное и экспоненциальное, логнормальное и др. Поэтому часто целью экспериментальных исследований является определение закона распределения случайных величин по экспериментальным данным.

Дата добавления: 2014-11-18