Приклад 8.5

Нехай було проведено 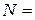500 вимірювань деякої випадкової величини. Всі вони належать інтервалу від 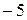до +5. Необхідно побудувати статистичний ряд. Кількість розрядів 10.

Розв‘язання.

Згідно з умовами завдання увесь діапазон було поділено на 10 інтервалів (розрядів) і підраховано число величин які улучили у кожний з них. Результати зведено у таблицю 8.5 (три верхніх рядки), де 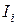– відповідний інтервал гру пування; 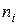–кількість величин у відповідному інтервалі; 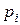– ймовірність (частота) попадання в інтервал 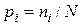. Про оцінки, які наведені у четвертому і п‘ятому рядках, мова буде нижче.

Таким чином інформація, яку було зосереджено у простому статистичному ряді (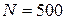) завдяки групуванню містиця тепер у статистичному ряді обсягом 10.

É

Статистический ряд часто оформляется графически в виде так называемой гистограммы. Гістограма будується так. За віссю абсцис відкласти розряди (інтервали 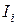) і на кожному з них будується прямокутник такий, що його площина дорівнює або 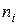і тоді сумарна площина дорівнює 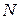(така гістограма є гістограмою чисельності), або його площина дорівнює 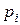і тоді сумарна площина дорівнює 1 (така гістограма є гістограмою ймовірності).

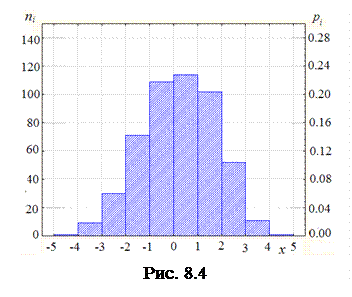В качестве иллюстрации отображения статистического ряда графически на рис. 8.4 наведено обидві ці гістограми, построенные по данным, полученным в примере 8.5, на одному графіку. Та шкала, що наведена ліворуч, характеризує гістограму чисельності, та, що наведена праворуч,– гістограму ймовірності.

Очевидно, при увеличении числа опытов 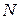можно выбирать все более и более мелкие разряды; при этом гистограмма вероятности будет все более приближаться к некоторой кривой, ограничивающей площадь, равную единице. Нетрудно убедиться, что эта кривая представляет собой график плотности⁵ распределения величины X.

Пользуясь данными статистического ряда, можно приближенно построить я статистическую функцию распределения величины X.

Вправа 8.8

Обчисліть і побудуйте графік функції розподілу випадкової величини за даними, що наведені у табл.. 8.5.

8.4.3. Выравнивание статистических рядов

Во всяком статистическом распределении неизбежно присутствуют элементы случайности, связанные с тем, что число наблюдений ограничено, что произведены именно те, а не другие опыты, давшие именно те, а не другие результаты. Только при очень большом числе наблюдений эти элементы случайности сглаживаются, и случайное явление, обнаруживает в полной мере присущую ему закономерность. На практике мы почти никогда не имеем дела с таким большим числом наблюдений и вынуждены считаться с тем, что любому статистическому распределению свойственны в большей или меньшей мере черты случайности. Поэтому при обработке статистического материала часто приходится решать вопрос о том, как подобрать для данного статистического ряда теоретическую кривую распределения, выражающую лишь существенные черты статистического материала, но не случайности, связанные с недостаточным объемом экспериментальных данных. Такая задача называется задачей выравнивания (сглаживания) статистических рядов.

Задача выравнивания заключается в том, чтобы подобрать теоретическую плавную кривую распределения, с той или иной точки зрения наилучшим образом описывающую данное статистическое распределение.

Задача о наилучшем выравнивании статистических рядов, как и вообще задача о наилучшем аналитическом представлении эмпирических функций, есть задача в значительной мере неопределенная, и решение ее зависит от того, что считается «наилучшим». Например, при сглаживании эмпирических зависимостей часто используют метод наименьших квадратов (см. раздел 7), считая, что наилучшим приближением к эмпирической зависимости в данном классе функций является такое, при котором сумма квадратов отклонений обращается в минимум. При этом вопрос о том, в каком именно классе функций следует искать наилучшее приближение, решается уже не из математических соображений, а из соображений, связанных с физикой решаемой задачи с учетом характера полученной эмпирической кривой и степени точности произведенных наблюдений. Часто принципиальный характер функции, выражающей исследуемую зависимость, известен заранее из теоретических соображений, из опыта же требуется получить лишь некоторые численные параметры, входящие в выражение функции; именно эти параметры подбираются с помощью метода наименьших квадратов.

Аналогично обстоит дело и с задачей выравнивания статистиче­ских рядов. Как правило, принципиальный вид теоретической кривой выбирается заранее из соображений, связанных с существом задачи, а в некоторых случаях просто с внешним видом статистического распределения. Аналитическое выражение выбранной кривой распределения зависит от некоторых параметров. Задача выравнивания статистического ряда переходит в задачу рационального выбора тех значений параметров, при которых соответствие между статистическим и теоретическим распределениями оказывается наилучшим.

Предположим, например, что исследуемая величина Х есть ошибка измерения, возникающая в результате суммирования воздействий множества независимых элементарных ошибок; тогда из теоретических соображений можно считать, что величина X подчиняется нормальному закону:

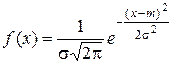, (8.15)

и задача выравнивания переходит в задачу о рациональном выборе параметров 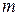и .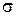

Бывают случаи, когда заранее известно, что величина X распределяется статистически приблизительно равномерно на некотором интервале (например распределение значений начальной фазы узкополосного гауссова случайного процесса). Тогда можно поставить задачу о рациональном выборе, параметров этого закона равномерной плотности

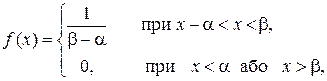
которым можно наилучшим образом заменить (выровнять) заданное статистическое распределение.

Следует при этом иметь в виду, что любая аналитическая функция 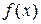, с помощью которой выравнивается статистическое распределение, должна обладать основными свойствами плотности распределения:

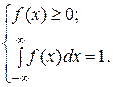(8.16)

Предположим, что, исходя из тех или иных соображений, нами выбрана функция 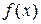, удовлетворяющая условиям (8.16), с помощью которой мы хотим выровнять данное статистическое распределение. В выражение этой функции входит несколько параметров 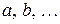. Требуется подобрать эти параметры так, чтобы функция 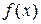наилучшим образом описывала данный статистический материал. Один из методов, применяемых для решения этой задачи, – это так называемый метод моментов.

Согласно методу моментов параметры 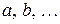выбираются с таким расчетом, чтобы несколько важнейших числовых характеристик (моментов) теоретического распределения были равны соответствующим статистическим характеристикам. Например, если теоретическая кривая 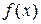зависит только от двух параметров 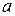и 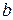, эти параметры выбираются так, чтобы математическое ожидание 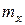и дисперсия 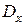теоретического распределения совпадали с соответствующими статистическими характеристиками, полученными обработкой опытных данных и т. д.

Следует заметить, что при выравнивании статистических рядов нерационально пользоваться моментами порядка выше четвертого, так как точность вычисления моментов резко падает с увеличением их порядка.

Дата добавления: 2014-11-18