Предельные значения нормированных отклонений опытного распределения от значений теоретического распределения для заданных доверительных вероятностей

Порядок выполнения работы

1. Из табл. 1 приложения студенту необходимо выписать исходные данные в соответствии с вариантом, выданным преподавателем.

Таблица 33

γ		γ
0,01	0,44	0,60	0,89
0,05	0,52	0,70	0,97
0,10	0,57	0,80	1,07
0,15	0,61	0,90	1,22
0,20	0,65	0,95	1,36
0,30	0,71	0,98	1,52
0,40	0,77	0,99	1,63

По результатам испытаний требуется проверить гипотезу о нормальном распределении наработки до отказа.

Во время испытаний тормозных устройств были получены данные о наработке их до отказа. Распределение наработки до отказа тормозных устройств подчиняется нормальному закону.

Данные испытания, необходимые для построения функции опытного и теоретического распределения, приведены в табл. 1 приложения.

2. Результаты наблюдений случайной величины х, полученные в специально поставленном эксперименте, располагают в порядке их возрастания:

.

При группировании результатов испытаний выявляют наибольшее х и наименьшее х₁ значения. Зона рассеивания (размах) рассчитывается как разность между этими элементами.

Следовательно, в выборке х₁,…, х_N определяют размах:

3. Зону рассеивания делят на интервалы в количестве r, вычисленные по формуле:

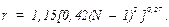
Полученное значение округляют в наименьшую сторону.

4. Ширина интервала группирования:

5. В первую графу (табл. 34) записывают значения х₁; х₁+Δ; х₁+2Δ;…х_r.

6. Вычисляют среднее арифметическое значение и среднее квадратическое отклонение:

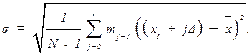
7. Данные вычислений заносят в графы 3… 6 табл. 34.

8. В седьмую графу табл. 34 записывают:

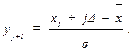
Таблица 34 Данные для построения функции опытного и теоретического распределения	F(yj+1)						r Σ J=0
FN(yj+1)
yj+1
_ ((x1+jΔ) -x)^- 2 mj+1
((x1+jΔ) -x) ^2
(x1+jΔ) –x
mj+1(x1+jΔ)
mj+1
x1+jΔ

9. В восьмую графу табл. 34 записывают эмпирическую функцию (функцию опытного распределения):

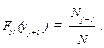
где 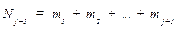, а в девятую графу табл. 34 – функцию теоретического распределения, которую находят по формуле (106) или по табл. 1.2 [15], принимая во внимание, что в нашем случае .

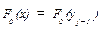Функция теоретического распределения F(y) представляет собой вероятность того, что при принятом распределении случайной величины y будет выполняться условие .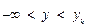

10. По формуле (110) определяем интенсивность отказов, а по формуле (111) – выборочную дисперсию. Значения интенсивности отказов и выборочной дисперсии заносят в табл. 35, где графы 1… 4 переносят из табл. 34.

Таблица 35

Дата добавления: 2014-11-18