Порядок выполнения работы. 1. Из табл. 2 приложения студенту необходимо выписать исходные данные в соответствии с вариантом, выданным преподавателем

1. Из табл. 2 приложения студенту необходимо выписать исходные данные в соответствии с вариантом, выданным преподавателем.

В результате испытаний технических систем записывалась их наработка, после которой каждая из них подлежала капитальному ремонту. Полученные результаты были сгруппированы по интервалам продолжительностью h = 350 моточасов.

Данные о числе образцов, подлежащих капитальному ремонту в первом, втором и т.д. интервалах наработки, взятые из табл. 2 приложения, заносят в первую и вторую графы табл. 37. Требуется проверить гипотезу о том, что указанная наработка подчинена экспоненциальному распределению.

Таблица 37

Данные для проверки согласия опытного распределения наработки технических систем до капитального ремонта с экспоненциальным распределением

j

mj

(j-1/2)mj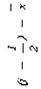

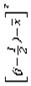
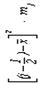
yj

yj – y1

F(yj – y1)

Pj

Pjn

mj – Pjn

(mj – Pjn)^2

(mj­Pjn)²Pjn

.

.

r

Σ

Σ

Σ

2. На практике результаты наблюдений случайной величины х, полученные на основании выбора статистических данных, располагают в порядке возрастания:

.

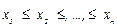3. Далее вычисляют размах x_n – x1 и образуют r равных интервалов шириной h:

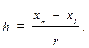
В предполагаемом примере, ввиду большого числа данных, значения х₁ … x_n не представлены, а известны значения m_j, r и h (m_j – это частоты величин x_j, попавшие в j -е интервалы; h – ширина интервала; r – число интервалов).

4. При обработке результатов наблюдений, необходимых для оценки предполагаемой гипотезы по критерию χ², заполняют графы 3…14 табл. 37.

5. Вычисляют среднее арифметическое значение и среднее квадратическое отклонение:

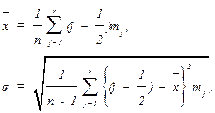
где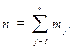

6. Полученные значения 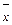и σ исследуемой наработки, измеренные числом интервалов, надо для перевода в моточасы умножить на h.

Поскольку для экспоненциального распределения математическое ожидание равно среднему квадратическому отклонению, то начало отсчета наработки при определении нормированных величин y_j сдвинуто на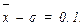

7. Вычисляют величины

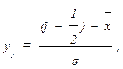
их записывают в седьмую графу табл. 37.

8. В восьмой графе табл. 37 вычисляют разность y_j – y₁.

9. В девятую графу табл. 37 записывают значения функции проверяемого теоретического распределения F(y_j – y₁)

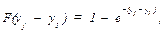
где значение 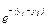переписывают из специальных таблиц [15].

10. В десятую графу табл. 37 записывают вероятности попадания опытных данных в j -й интервал P_j: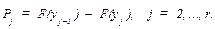

11. Заполняют графу 11, если в ней окажутся значения nP_j < 10, то следует объединить интервал, в котором ожидаемое число результатов наблюдений меньше десяти, с одним или несколькими соседними интервалами таким образом, чтобы в новом интервале ожидаемое число результатов наблюдений было не менее десяти.

Объединение интервалов пояснено на примере, где после заполнения табл. 37, получены некоторые данные:

		58,5	10,9	118,81		1,28	2,23	0,8925	0,0121	4,34	-1,34		0,242
		61,5	11,9	141,61		1,40	2,35	0,9046	0,0108	3,87	-0,65	0,42	0,036
											-0,87	0,75	0,194
		107,5	12,9	166,41		1,50	2,47	0,9154	0,0096	3,44	1,56	2,43	0,707
			13,9	193,21		1,64	2,59	0,9250	0,0078	2,79	1,21	1,46	0,524
			14,9	222,01		1,75	2,70	0,9328	0,0076		-0,72	0,51	0,187
											3,94	15,52	1,54
		73,5	15,9	252,81		1,87	2,82	0,9404	0,0067	2,40	0,60	0,36	0,15
		127,5	16,9	320,41		1,99	2,94	0,9471	0,0060	2,15	2,85	8,12	3,78

Видно, что объединены 20…22 и 23…26 интервалы. При этом для всех расширенных интервалов значения n(P₂₀ + P₂₁ + P₂₂) и n(P₂₃ + P₂₄ + P₂₅ + P₂₆) более 10. эти интервалы заключают в полужирную рамку.

Соответственно вычисляют и все остальные величины, например, графа 14 табл. 37 приобретает следующий вид:

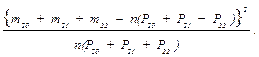
12. После объединения интервалов считают полное число неравновеликих интервалов (вместо равновеликих), и число степеней свободы при оценке χ² принимают равным k = N – 1, где N – число неравновеликих интервалов.

13. Вычислить критерий χ²:

.

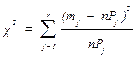14. Задать доверительную вероятность

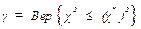
того, что величина χ², полученная вследствие случайных отклонений частостей опытного распределения от соответствующих вероятностей теоретического распределения будет меньше значения 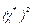, установленного для доверительной вероятности γ.

15. По таблице [15] квантилей x_u – квадрат распределения 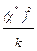при доверительной вероятности γ находят дл опытных число степеней свободы 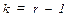и 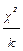ближайшее значение доверительной вероятности.

Или по таблице [15] для доверительной вероятности и числа степеней свободы 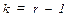находят величину 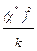, вычисляют 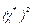и сравнивают с ним вычисленную по данным табл. 37 величину χ².

16. Если χ² окажется меньше 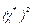, то для принятой доверительной вероятности гипотеза о согласии опытного и теоретического распределений принимается, в противном случае – отвергается.

17. Построить графики функций теоретического и опытного распределений, привести расчеты, заполнить таблицы. Сделать вывод о принятии или непринятии гипотезы о согласии наработки технической системы до капитального ремонта с экспоненциальным распределением.

18. Отчет защитить у преподавателя.

Контрольные вопросы

1. Чему равно математическое ожидание для экспоненциального распределения?

2. Что такое ранжированный ряд?

3. Как вычислить критерий χ²?

4. Какое распределение называют экспоненциальным?

5. В каком случае применяют экспоненциальное распределение?

6. Чему равна дисперсия для экспоненциального распределения?

7. Как определить вероятность безотказной работы до наработки t?

Приложение

Таблица 1

Дата добавления: 2014-11-18