Основные теоретические сведения. Применение критерия χ2 для экспоненциального закона распределении

Практическая работа № 10

Применение критерия χ² для экспоненциального закона распределении

Ц е л ь р а б о т ы: проверить согласие опытного и теоретического распределения случайной величины с применением критерия χ².

Н е о б х о д и м о е о б о р у д о в а н и е: микрокалькулятор; таблица исходных данных.

Распределение случайной положительной величины называется экспоненциальным, если его плотность вероятности имеет вид:

,

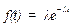где λ – постоянная (параметр распределения).

Функция этого распределения

.

Если t – наработка, то вероятность безотказной работы до наработки t:

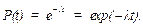
Для вычислений существуют табличные значения функции exp(x) /

Квантили экспоненты z_p:

.

Математическое ожидание и дисперсию находят по следующим уравнениям:

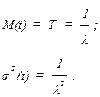
Коэффициент вариации для экспоненциального распределения:

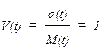
Критерий χ². Пусть m_j и Р_j – частости и вероятности появления события A_j(j = 1,…,r) в N независимых испытаниях соответственно.

Тогда при больших N величина

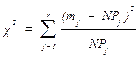
асимптотически подчинена распределению χ² с числом степеней свободы k = r – 1. если в качестве события рассматривать попадание j -го результата наблюдений в интервал (j – 1)h, jh, то при

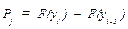
приведенное выражение χ² можно рассматривать как критерий согласия опытного и теоретического распределений.

Для нахождения χ² нужно вычислить математическое ожидание NP_j, для чего определить 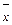и σ для среднего значения квадратического отклонения проверяемого теоретического распределения.

Рекомендуется вычислить 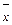и σ по группированным значениям x и затем для σ использовать поправку Шеппарда. При этом все x из интервала (j – 1)h, jh нужно считать сконцентрированными в средней точке этого интервала 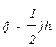С помощью таких модифицированных значений нужно вычислить 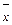и σ. Для того, чтобы можно было применять поправку Шеппарда, нужно, чтобы все интервалы имели одинаковую длину h.

Если имеется много интервалов, и их середины находятся очень близко друг к другу, то необходимость в применении поправок Шеппарда отпадает.

Второе условие применения критерия χ² – назначение числа степеней свободы. Распределение χ² с r – 1 степенями свободы имеет место в том случае, если выражение

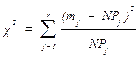
было вычислено с помощью истинных значений 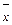и σ. Правильный выбор числа степеней свободы зависит от объема выборки N и числа интервалов r.

Теория применения критерия χ² основана на том, что величины (m_j, NР_j) приближенно распределены нормально. Это имеет место, если величины NР_j > 10. Если некоторое значение NР_j < 10, то необходимо объединять маленькие группы, чтобы каждая из них после объединения содержала по крайней мере 10 ожидаемых результатов. Если наблюдений так мало, что этого сделать нельзя, критерий χ² применять нецелесообразно.

Дата добавления: 2014-11-18